 |
7. Многомерные случайные величины и их числовые характеристики
|
|
|
|
7. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Основные понятия раздела
Системы случайных величин будем обозначать прописными буквами греческого алфавита, а их элементы – прописными буквами латинского алфавита: 
, 
, …
Пусть дан вектор СВ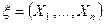 
и вектор действительных чисел 
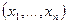. Функцию 
называют n-мерной функцией распределения СВ .
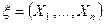Свойства функции распределения многомерной случайной величины.
FF1. Функция распределения вероятностей многомерной случайной величины – неубывающая функция своих аргументов.
FF2. Функция 
является ограниченной (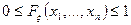 
):
– 
, если хотя бы один ее аргумент 
;
– 
, если все ее аргументы 
.
FF3. Функция непрерывна слева по каждому аргументу.
FF4. Если известна функция распределения вероятностей системы случайных величин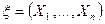 
, то может быть найдена функция распределения любой ее подсистемы: 
, где 
.
Если существует такая функция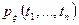 
, что при любых 
имеет место равенство:
,
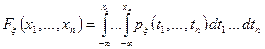то эта функция называется плотностью распределения вероятностей системы случайных величин ξ . При этом почти всюду имеет место равенство:
.
Математическое ожидание вида: 
называется n – мерным моментом 
-го порядка случайного вектора относительно вектора констант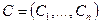 
.
При 
момент 
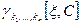называют центральным и обозначают: 
.
При 
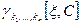момент называют начальным и обозначают: 
.
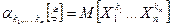Характеристика случайных величин X и Y вычисляемая по формуле:
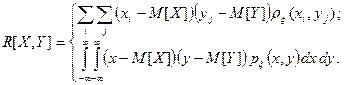
называется корреляционным моментом (моментом связи этих случайных величин). Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеивания величин X и Y относительно математических ожиданий, еще и связь между ними.
Для улавливания степени связи X и Y в “чистом виде” переходят от корреляционного момента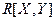 
к безразмерной характеристике (коэффициенту корреляции): 
, где 
.
|
|
|
В общем случае n-мерная случайная величина может быть охарактеризована при помощи:
1) математических ожиданий: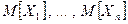 
;
2) дисперсий: 
;
3) корреляционных моментов 
, которые можно свести в корреляционную матрицу
,
где 
, или матрицу коэффициентов корреляции
;
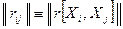4) начальных и центральных моментов более высоких порядков;
5) абсолютных начальных и центральных моментов любого порядка.
Задачи с решениями
1. Двумерная случайная величина 
имеет плотность распределения вероятностей: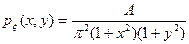 
. Найти величину A, функцию распределения 
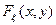, вероятность попадания случайной точки 
в квадрат, заданный прямыми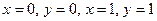 
.
Решение. Для определения величины A используем свойство плотности, называемое условием нормировки: 
. Применив это условие для нашего случая, запишем уравнение:
.
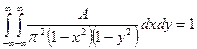Проинтегрировав и подставив пределы, получаем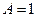 
.
Функцию распределения вероятностей найдем по определению
.
.
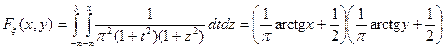Вероятность попадания случайной точки в заданный квадрат вычислим, используя свойство плотности распределения вероятностей:
.
2. Распределение вероятностей случайной величины задано таблицей:
 X
Y
| ||||
| 2, 3 | 0, 05 | 0, 12 | 0, 08 | 0, 04 |
| 2, 7 | 0, 09 | 0, 3 | 0, 11 | 0, 21 |
Найти законы распределения составляющих и корреляционный момент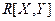 
.
Решение. Для нахождения законов распределения составляющих, воспользуемся следующим свойством:
и 
.
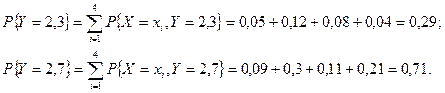
Проверим условие нормировки:
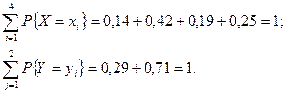
По определению
.
;
;
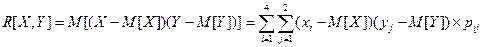3. Найти плотность распределения и вероятность попадания случайной точки в прямоугольник, ограниченный прямыми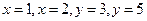 
, если известна функция распределения:
Решение. По определению 
.
Для определения требуемой вероятности воспользуемся свойством функции распределения для абсолютно непрерывных случайных величин:
|
|
|
.
Подставляя значения границ интервалов, имеем
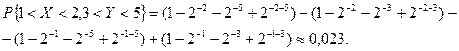
4. Положительная двумерная случайная величина задана функцией распределения вероятностей
Найти плотности распределения составляющих 
, 
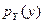и начальные моменты 
, 
, 
.
Решение. Воспользовавшись определением для нахождения плотности распределения величины 
, получим:
.
Для вычисления плотностей распределения составляющих, применим следующее свойство: 
; 
. В нашем случае имеем
;
.
Начальные моменты , и найдем по определению.
; 
;
.
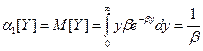5. Распределение вероятностей случайной величины задано таблицей:
| X
Y
| -1 | ||
| 0, 10 | 0, 15 | 0, 20 | |
| 0, 15 | 0, 25 | 0, 15 |
Найти вероятность того, что X примет значение большее 0 и центральные моменты 
, 
и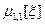 
.
Решение. Прежде, чем отыскать требуемую вероятность, запишем распределение вероятностей случайной величины X:
| -1 | ||
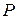
| 0, 25 | 0, 40 | 0, 35 |
Тогда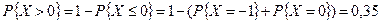 
.
Центральные моменты вычислим по определению
.
Запишем распределение случайной величины Y:
| ||
|
| 0, 45 | 0, 55 |
Найдем 
и 
:
;
.
Далее находим
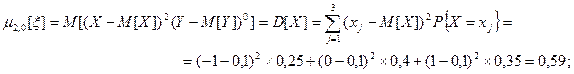
6. Случайная величина задана плотностью распределения вероятностей:
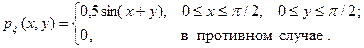
Определить: а) функцию распределения системы; б) математические ожидания и ; в) построить матрицу коэффициентов корреляции.
Решение.
а) Функцию распределения найдем по определению, применив его для нашего случая:
.
б) Математическое ожидание случайной величины
.
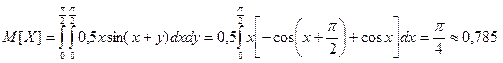В силу симметрии плотности распределения вероятностей относительно X и Y следует, что 
.
в) Коэффициент корреляции находится по формуле:
.
Вычислим дисперсию случайной величины X
В силу симметрии плотности распределения вероятностей относительно X и Y имеем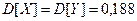 
.
Корреляционный момент
В нашем случае получаем
Таким образом, матрица коэффициентов корреляции имеет вид
.
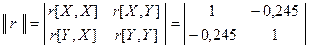7. Определить плотность распределения вероятностей и начальный момент третьего порядка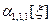 
системы случайных величин 
, заданных функцией распределения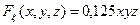 
при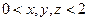 
.
Решение. По определению 
. Тогда для нашего случая имеем
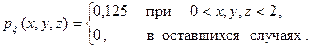
Начальный момент третьего порядка вычислим по формуле:
8. Даны математические ожидания двух нормальных случайных величин 
, 
и матрица корреляционных моментов
.
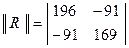Определить плотность распределения вероятностей системы .
|
|
|
Решение. Известно, что 
. Отсюда получаем:
;
;
.
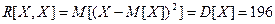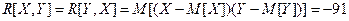Определим коэффициент корреляции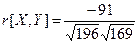 
. Запишем плотность распределения системы, используя формулу двумерного нормального распределения
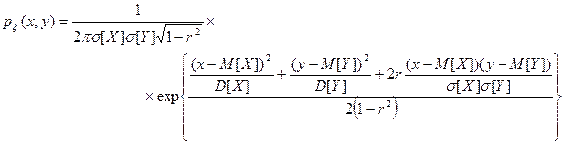
и подставляя в нее найденные значения параметров:
.
9. Двумерная случайная величина подчинена закону распределения с плотностью 
в области D и 
вне этой области. Область D – треугольник, ограниченный прямыми 
, 
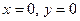. Найти величину A и вероятность того, что 
.
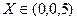Решение. Величину A найдем по свойству плотности (условие нормировки), применив его к условию задачи:
.
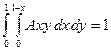Решив это уравнение, получаем 
.
Для определения необходимой вероятности, прежде найдем распределение величины X:
;
.
10. Пусть X и Y случайные величины, имеющие конечные моменты второго порядка. Показать, что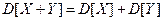 
тогда, и только тогда, когда эти величины некоррелированы.
Решение. По определению 
. Преобразуем это выражение:
Отсюда видно, что 
тогда и только тогда, когда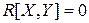 
, т. е. когда случайные величины X и Y некоррелированы. Что и требовалось показать.
|
|
|
