 |
Задачи для самостоятельной работы
|
|
|
|
7. 1. Определить плотность распределения вероятностей системы трех случайных величин  по заданной функции распределения:
по заданной функции распределения:
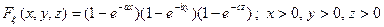 .
.
7. 2. Определить вероятность попадания точки с координатами 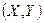 в область, заданную неравенствами (
в область, заданную неравенствами (  ), если функция распределения системы
), если функция распределения системы 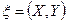 имеет вид
имеет вид  :
:

7. 3. Дискретная случайная величина 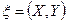 задана таблицей:
задана таблицей:
 X
Y X
Y
| ||
| -1 | 0, 10 | 0, 20 |
| 0, 20 | 0, 30 | |
| 0, 20 |
Найти законы распределения составляющих и центральные моменты двух первых порядков величины  .
.
7. 4. Координаты случайной точки 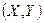 распределены равномерно внутри прямоугольника, ограниченного абсциссами
распределены равномерно внутри прямоугольника, ограниченного абсциссами  и ординатами
и ординатами 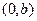 . Определить вероятность попадания случайной точки в круг радиуса R, если
. Определить вероятность попадания случайной точки в круг радиуса R, если  , а центр круга совпадает с началом координат.
, а центр круга совпадает с началом координат.
7. 5. Найти начальные моменты двух первых порядков случайной величины 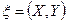 , заданной таблицей:
, заданной таблицей:
 X
Y X
Y
| ||
| -1 | 0, 10 | 0, 15 |
| 0, 15 | 0, 25 | |
| 0, 20 | 0, 15 |
7. 6. Задана плотность совместного распределения двумерной случайной величины 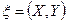

Найти математические ожидания и дисперсии составляющих.
7. 7. Случайная величина X есть сумма трех случайный величин:  ,
,  ,
,  ,
,  ,
,  ,
, 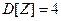 ,
,  ;
;  ;
;  ;
; 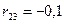 . Найти
. Найти  и
и  .
.
7. 8. Совместное распределение величин X и Y задано таблицей:
 X
Y X
Y
| -1 | ||
| -1 | 1/8 | 1/12 | 7/24 |
| 7/24 | 1/12 | 1/8 |
Найти: а) одномерные распределения величин X и Y; б) математические ожидания и дисперсии величин X и Y.
7. 9. Совместное распределение величин X и Y является равномерным в единичном круге  . Найти вероятность
. Найти вероятность 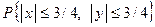 .
.
7. 10. Система случайных величин 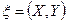 задана таблицей:
задана таблицей:
 X
Y X
Y
| |||||||
| 0, 202 | 0, 174 | 0, 113 | 0, 062 | 0, 049 | 0, 023 | 0, 004 | |
| 0, 099 | 0, 064 | 0, 040 | 0, 031 | 0, 020 | 0, 006 | ||
| 0, 031 | 0, 025 | 0, 018 | 0, 013 | 0, 008 | |||
| 0, 001 | 0, 002 | 0, 004 | 0, 011 |
а) Найти функцию распределения системы 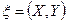 .
.
|
|
|
б) Определить вероятность 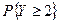 .
.
в) Найти  и
и  .
.
7. 11. Плотность распределения вероятностей системы случайных величин 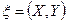 имеет вид:
имеет вид:

Определить постоянную c и вероятность попадания в круг радиуса  с центром в начале координат.
с центром в начале координат.
7. 12. Система случайных величин 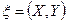 в интервалах
в интервалах  и
и 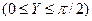 задана функцией распределения вероятностей
задана функцией распределения вероятностей
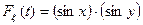 .
.
Найти: а) плотность распределения системы 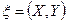 ; б) математические ожидания величин X и Y; в) корреляционную матрицу системы.
; б) математические ожидания величин X и Y; в) корреляционную матрицу системы.
7. 13. Распределение вероятностей дискретной случайной величины 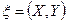 задано таблицей:
задано таблицей:
 X
Y X
Y
| |||
| 0, 17 | 0, 13 | 0, 25 | |
| 0, 10 | 0, 30 | 0, 05 |
Найти законы распределения составляющих и корреляционную матрицу системы.
7. 14. Доказать, что коэффициент корреляции по абсолютной величине не превосходит единицы.
7. 15. Дана матрица корреляционных моментов системы трех случайных величин  :
:
 .
.
Составить матрицу коэффициентов корреляции системы  .
.
7. 16. Определить математические ожидания и корреляционную матрицу системы случайных величин 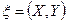 , заданной плотностью распределения вероятностей
, заданной плотностью распределения вероятностей  .
.
7. 17. Плотность распределения координат случайной точки на плоскости имеет вид:  . Требуется определить: а) величину c; б) корреляционную матрицу системы.
. Требуется определить: а) величину c; б) корреляционную матрицу системы.
7. 18. Определить в точке (2, 2) плотность распределения вероятностей системы двух нормальных случайных величин 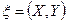 , для которых
, для которых  и
и 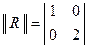 .
.
7. 19. Случайные величины X и Y некоррелированы. Доказать, что  .
.
7. 20. Случайные величины X, Y и Z попарно некоррелированы. Верно ли равенство 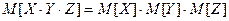 ?
?
7. 21. Система случайных величин 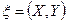 имеет плотность распределения вероятностей:
имеет плотность распределения вероятностей:  . Определить величину A и найти функции распределения составляющих системы
. Определить величину A и найти функции распределения составляющих системы 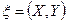 .
.
7. 22. Координаты 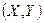 случайной точки A на плоскости подчинены нормальному закону
случайной точки A на плоскости подчинены нормальному закону  . Определить вероятность того, что точка A окажется внутри эллипса с главными полудиаметрами ka и kb, совпадающими с координатными осями Ox и Oy.
. Определить вероятность того, что точка A окажется внутри эллипса с главными полудиаметрами ka и kb, совпадающими с координатными осями Ox и Oy.
|
|
|
7. 23. Распределение вероятностей случайной величины 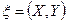 задано формулами:
задано формулами:
 .
.
Найти: а) M[X] и M[Y]; б) M[X|Y]; в) r[X, Y].
7. 24. Случайные величины X и Y независимы и нормально распределены с одними и теми же параметрами a и σ . Найти коэффициент корреляции величин aX+bY и aX-bY.
7. 25. Случайные величины 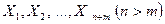 независимы, одинаково распределены и имеют конечную дисперсию. Найти коэффициент корреляции между суммами
независимы, одинаково распределены и имеют конечную дисперсию. Найти коэффициент корреляции между суммами 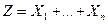 и
и 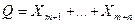 .
.
|
|
|


