 |
8. Независимость случайных величин. Условные законы распределения вероятностей
|
|
|
|
8. НЕЗАВИСИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН. УСЛОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
Основные понятия и теоремы раздела
Случайные величины X и Y называются независимыми если, для любых полуинтервалов  и
и  события
события 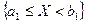 и
и  являются независимыми, т. е.
являются независимыми, т. е. 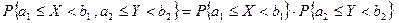 .
.
Для системы дискретных случайных величин ξ =(X, Y) независимость означает, что совместное распределение вероятностей задается соотношением:
 .
.
В случае непрерывно распределенных случайных величин X и Y условие независимости принимает следующий вид:
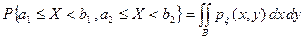 ,
,
где 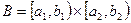 ;
; 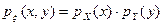 .
.
Случайные величины называются независимыми если,  , где
, где  .
.
Теорема. Пусть  – вектор с независимыми случайными компонентами. Если
– вектор с независимыми случайными компонентами. Если  есть функции распределения абсолютно непрерывного типа при каждом
есть функции распределения абсолютно непрерывного типа при каждом  , то и
, то и  есть также функция распределения абсолютно непрерывного типа. Обратно, если
есть также функция распределения абсолютно непрерывного типа. Обратно, если  абсолютно непрерывна, то и
абсолютно непрерывна, то и  тоже абсолютно непрерывны для всех
тоже абсолютно непрерывны для всех  . При этом
. При этом 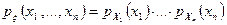 почти всюду, где
почти всюду, где 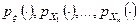 – плотности соответственно для
– плотности соответственно для 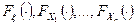 .
.
Условным законом распределения вероятностей (УЗРВ) случайной величины X, входящей в систему  , называется ее закон распределения вероятностей, вычисленный при условии, что другие компоненты вектора
, называется ее закон распределения вероятностей, вычисленный при условии, что другие компоненты вектора 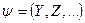 приняли определенные значения
приняли определенные значения 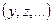 . УЗРВ можно задавать как функцией распределения вероятностей
. УЗРВ можно задавать как функцией распределения вероятностей 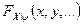 , так и плотностью распределения
, так и плотностью распределения  .
.
Если X и Y – дискретные случайные величины, то условное распределение  , определяется как
, определяется как
 ,
,
а условное распределение  как
как
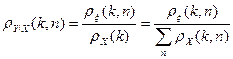 ,
,
где  – совместное распределение вероятностей случайных величин X и Y, составляющих вектор
– совместное распределение вероятностей случайных величин X и Y, составляющих вектор 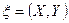 , и
, и
 ,
,  .
.
Для непрерывных случайных величин X и Y условные плотности распределения имеют вид:
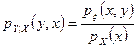 ,
,  ,
,
где  – совместная плотность распределение вероятностей случайных величин X и Y, и
– совместная плотность распределение вероятностей случайных величин X и Y, и
|
|
|
 ,
,  .
.
Случайная величина X не зависит от Y тогда и только тогда, когда ее условное распределение (при условии 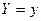 ) не зависит от y и совпадает с исходным (безусловным) распределением.
) не зависит от y и совпадает с исходным (безусловным) распределением.
Задачи с решениями
1. Дискретная случайная величина  задана таблицей:
задана таблицей:
 X
Y X
Y
| ||
| 0, 25 | 0, 1 | |
| 0, 15 | 0, 05 | |
| 0, 32 | 0, 13 |
Найти условный закон распределения вероятностей X при условии, что Y=10 и условный закон распределения вероятностей Y при условии, что X=6.
Решение. По определению условный закон в виде ряда распределения записывается следующим образом:
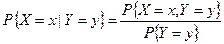 ;
;  .
.
Вычислим вероятность  , и применим записанную выше формулу для определения требуемого условного распределения.
, и применим записанную выше формулу для определения требуемого условного распределения.
 ;
;  .
.
Условие нормировки выполняется: 5/7+2/7=1.
Вероятность  , тогда требуемое условное распределение примет вид:
, тогда требуемое условное распределение примет вид:
 ;
;
 ;
;
 .
.
Условие нормировки выполняется: 10/28+5/28+13/28=1.
2. Совместное распределение случайных величин X и Y задано таблицей:
 X
Y X
Y
| -1 | ||
| 1/27 | 8/27 | ||
| 1/27 | 8/27 | ||
| 8/27 | 1/27 |
Найти корреляционный момент системы и вероятность  .
.
Решение. Найдем безусловные законы распределения величин X и Y и условный закон  .
.
| X | -1 | ||
| P | 1/3 | 1/3 | 1/3 |
| Y | |||
| P | 1/3 | 1/3 | 1/3 |
| X | -1 | ||
| P{X|Y=4} | 1/9 | 8/9 |
Искомая вероятность 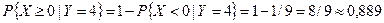 .
.
Корреляционный момент  . Найдем
. Найдем 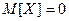 и
и  . Тогда
. Тогда

3. Положение случайной точки  равновероятно в любом месте эллипса с главными полудиаметрами a и b, совпадающими с осями координат
равновероятно в любом месте эллипса с главными полудиаметрами a и b, совпадающими с осями координат  и
и  соответственно. Требуется определить условные плотности распределения величин, входящих в систему.
соответственно. Требуется определить условные плотности распределения величин, входящих в систему.
Решение. Запишем плотность распределения вероятностей 

По определению условные плотности распределения компонент системы есть 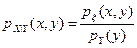 и
и  . Найдем плотности распределения каждой из координат. При
. Найдем плотности распределения каждой из координат. При 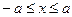 плотность
плотность 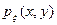 отлична от нуля только тогда, когда
отлична от нуля только тогда, когда  , значит
, значит
 .
.
Аналогично рассуждая, находим
|
|
|
 .
.
Теперь, применив определение, получаем

4. Задана плотность распределения вероятностей системы двух случайных величин  . Определить постоянную k, корреляционный момент
. Определить постоянную k, корреляционный момент 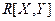 и условные плотности распределения случайных величин, входящих в систему.
и условные плотности распределения случайных величин, входящих в систему.
Решение. Для определения k используем условие нормировки:
 .
.
Отсюда  .
.
Корреляционный момент есть 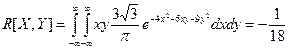 .
.
Найдем безусловные плотности распределения вероятностей составляющих.
 ;
;  .
.
Условные плотности распределения вероятностей случайных величин, входящих в систему, находим по определению:
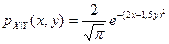 ;
;  .
.
5. Доказать, что если X и Y связаны линейной зависимостью 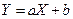 , то абсолютная величина коэффициента корреляции равна единице при
, то абсолютная величина коэффициента корреляции равна единице при  .
.
Решение. Корреляционный момент величин X и Y есть

Дисперсия величины Y есть

Найдем коэффициент корреляции величин X и Y

Что и требовалось доказать.
6. Плотность совместного распределения непрерывной двумерной случайной величины  в квадрате
в квадрате  ,
,  ; вне квадрата
; вне квадрата 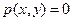 . Доказать, что составляющие X и Y независимы.
. Доказать, что составляющие X и Y независимы.
Решение. Случайные величины X и Y называются независимыми, если 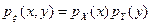 . Найдем плотности распределения величин X и Y.
. Найдем плотности распределения величин X и Y.
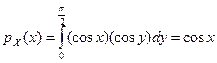 ;
;  .
.
Отсюда получаем, что 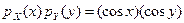 . Следовательно, случайные величины X и Y являются независимыми.
. Следовательно, случайные величины X и Y являются независимыми.
7. По мишени производится один выстрел. Вероятность попадания в мишень равна p. Рассматриваются две случайные величины: X – число попаданий; Y – число промахов. Построить функцию распределения 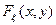 двумерной случайной величины
двумерной случайной величины  .
.
Решение. Случайные величины X и Y зависимы: X+Y=1. Пусть p – вероятность попадания в мишень и q=1-p – вероятность промаха, тогда таблица совместного распределения примет вид:
 X
Y X
Y
| ||
| p | ||
| q |
Отсюда функция распределения 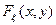 может быть записана следующим образом:
может быть записана следующим образом:
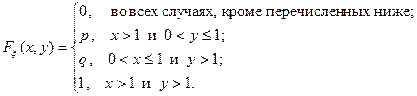
8. Система случайных величин  равномерно распределена внутри прямоугольного параллелепипеда, образованного плоскостями
равномерно распределена внутри прямоугольного параллелепипеда, образованного плоскостями  ,
, 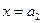 ,
,  ,
,  ,
,  ,
, 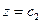 . Определить плотности распределения вероятностей подсистем
. Определить плотности распределения вероятностей подсистем  и
и 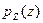 . Проверить зависимость случайных величин, входящих в систему.
. Проверить зависимость случайных величин, входящих в систему.
Решение. Запишем плотность распределения вероятностей системы  :
:

Для определения плотности распределения подсистемы  найдем интеграл
найдем интеграл 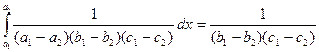 , и запишем плотность
, и запишем плотность

Плотность распределения вероятностей величины Z примет вид:
|
|
|
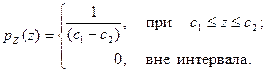
Аналогичным образом найдем
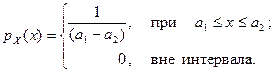
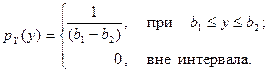
Теперь очевидно, что  , следовательно, случайные величины X, Y и Z независимы.
, следовательно, случайные величины X, Y и Z независимы.
9. Заданы плотности распределения вероятностей независимых составляющих непрерывной двумерной случайной величины  :
:


Найти плотность совместного распределения и функцию распределения вероятностей системы.
Решение. Для независимых случайных величин совместная плотность распределения вероятностей есть 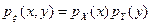 . В нашем случае получим
. В нашем случае получим
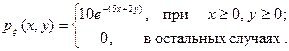
Функция распределения вероятностей
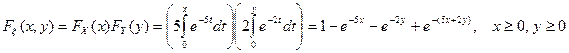 .
.
10. Случайные величины X и Y независимы и распределены по закону Бернулли:  . Найти
. Найти 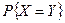 и
и  .
.
Решение. В силу независимости величин X и Y имеем
 ,
,
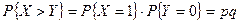 .
.
|
|
|


