 |
Задачи для самостоятельной работы
|
|
|
|
8. 1. Дискретная случайная величина  задана таблицей:
задана таблицей:
  Y
Y
| |||
| 0, 1 | 0, 15 | 0, 25 | |
| 0, 15 | 0, 25 | 0, 1 |
Найти условное распределение величины X при условии, что Y=2, и условное распределение Y при условии, что X=3.
8. 2. Дискретная случайная величина  задана таблицей:
задана таблицей:
  Y
Y
| |||
| 0, 4 | 0, 15 | 0, 3 | 0, 35 |
| 0, 8 | 0, 05 | 0, 12 | 0, 03 |
Найти условное математическое ожидание  и условную дисперсию
и условную дисперсию  .
.
8. 3. Плотность распределения вероятностей непрерывной двумерной случайной величины  имеет вид:
имеет вид: 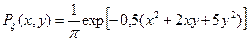 . Найти условные плотности распределения величин X и Y.
. Найти условные плотности распределения величин X и Y.
8. 4. Плотность распределения вероятностей непрерывной векторной случайной величины  имеет вид:
имеет вид: 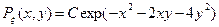 . Найти постоянный множитель C и условные плотности распределения вероятностей величин X и Y.
. Найти постоянный множитель C и условные плотности распределения вероятностей величин X и Y.
8. 5. Непрерывная двумерная случайная величина  распределена равномерно внутри прямоугольного треугольника с вершинами O(0; 0), A(0; 8), B(8, 0). Найти двумерную плотность распределения вероятностей системы и условные плотности распределения вероятностей составляющих X и Y.
распределена равномерно внутри прямоугольного треугольника с вершинами O(0; 0), A(0; 8), B(8, 0). Найти двумерную плотность распределения вероятностей системы и условные плотности распределения вероятностей составляющих X и Y.
8. 6. Задана плотность распределения вероятностей системы неотрицательных случайных величин X и Y: 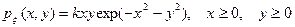 . Определить k,
. Определить k,  ,
,  ,
, 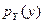 ,
,  .
.
8. 7. Плотность распределения вероятностей системы двух случайных величин  имеет вид:
имеет вид: 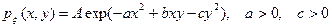 . Определить законы распределения
. Определить законы распределения  и
и 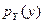 . При каких условиях X и Y являются независимыми случайными величинами?
. При каких условиях X и Y являются независимыми случайными величинами?
8. 8. Распределение вероятностей двумерного случайного вектора  задано таблицей:
задано таблицей:
|
Y | ||||||||||||||||||||||||
| -1 | 0, 001 | 0, 002 | 0, 005 | 0, 006 | 0, 014 | 0, 021 | 0, 021 | 0, 008 | 0, 002 | 0, 001 | ||||||||||||||
| 0, 001 | 0, 001 | 0, 002 | 0, 003 | 0, 008 | 0, 010 | 0, 040 | 0, 023 | 0, 012 | 0, 002 | |||||||||||||||
| 0, 002 | 0, 005 | 0, 010 | 0, 089 | 0, 154 | 0, 231 | 0, 180 | 0, 098 | 0, 048 | 0, 009
| |||||||||||||||
Найти условные распределения: Y при условии, что X=6, и X при условии, что Y=0, и корреляционную матрицу системы.
8. 9. Система независимых случайных величин  задана плотностями вероятностей
задана плотностями вероятностей  . Определить функцию распределения вероятностей этой системы случайных величин.
. Определить функцию распределения вероятностей этой системы случайных величин.
8. 10. Случайные величины X и Y связаны соотношением  , где m, n и c – неслучайные величины (
, где m, n и c – неслучайные величины ( 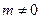 ,
, 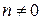 ). Найти: а) коэффициент корреляции
). Найти: а) коэффициент корреляции 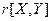 ; б) отношение среднеквадратических отклонений
; б) отношение среднеквадратических отклонений 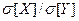 .
.
8. 11. Система двух случайных величин  подчиняется нормальному закону распределения
подчиняется нормальному закону распределения
 .
.
Определить: а) условные плотности распределения вероятностей случайных величин, входящих в систему; б) условные математические ожидания и дисперсии.
8. 12. Изготовляемые в цехе втулки сортируются на 4 группы по отклонению их внутреннего диаметра от нормального размера и на 4 группы по овальности втулок. Совместное распределение отклонений диаметра (X) и овальности втулок (Y) задано таблицей:
|
Y | 0, 01 | 0, 02 | 0, 03 | 0, 04 | ||||||
| 0, 002 | 0, 01 | 0, 02 | 0, 04 | 0, 04 | ||||||
| 0, 004 | 0, 03 | 0, 24 | 0, 15 | 0, 06 | ||||||
| 0, 006 | 0, 04 | 0, 10 | 0, 08 | 0, 08 | ||||||
| 0, 008 | 0, 02 | 0, 04 | 0, 03 | 0, 02 | ||||||
Найти: а) коэффициент корреляции между ними; б) распределение отклонений диаметра и условное распределение овальности при условии, что отклонение диаметра равно 0, 03; в) распределение овальности и условное распределение отклонения диаметра при условии, что овальность равна 0, 004.
8. 13. Случайные величины X и Y независимы и нормально распределены с параметрами  ,
,  . Найти вероятность того, что случайная точка (X, Y) попадет в кольцо
. Найти вероятность того, что случайная точка (X, Y) попадет в кольцо  .
.
8. 14. Положение случайной точки (X, Y) равно возможно в любом месте круга радиуса R, центр которого совпадает с началом координат. Определить плотность распределения вероятностей и функцию распределения вероятностей каждой из прямоугольных координат X и Y. Являются ли случайные величины X и Y независимыми?
|
|
|
8. 15. Система случайных величин X и Y подчинена равномерному закону распределения вероятностей внутри квадрата со стороной a. Диагонали квадрата совпадают с осями координат. Определить плотность распределения системы и условные плотности распределения вероятностей составляющих, проверить их зависимость и коррелированность.
8. 16. Случайные величины X, Y и Z равномерно распределены внутри сферы радиуса R. Определить для точек, лежащих внутри сферы, плотность распределения вероятностей координаты Z и условную плотность  .
.
8. 17. Для системы случайных величин  известны
известны 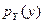 ,
,  и
и  . Определить
. Определить  и
и  .
.
8. 18. Положение ориентира на плоскости распределено по нормальному закону с параметрами  м,
м,  м,
м,  м,
м,  м,
м,  . Координата X определяет отклонение ориентира " по дальности", т. е. по направлению, параллельному линии наблюдения. Координата Y определяет отклонение ориентира " по боковому направлению", перпендикулярному линии наблюдения. Определить условную плотность распределения вероятностей отклонений ориентира по дальности при отсутствии боковых отклонений и условную плотность распределения вероятностей отклонений ориентира по боковому направлению при отклонении по дальности +25 м.
. Координата X определяет отклонение ориентира " по дальности", т. е. по направлению, параллельному линии наблюдения. Координата Y определяет отклонение ориентира " по боковому направлению", перпендикулярному линии наблюдения. Определить условную плотность распределения вероятностей отклонений ориентира по дальности при отсутствии боковых отклонений и условную плотность распределения вероятностей отклонений ориентира по боковому направлению при отклонении по дальности +25 м.
8. 19. Координаты случайной точки на плоскости подчиняются нормальному закону распределения вероятностей
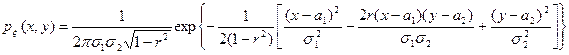 .
.
Определить условные плотности  ,
,  , условные математические ожидания и условные дисперсии.
, условные математические ожидания и условные дисперсии.
8. 20. Непрерывная двумерная случайная величина  распределена равномерно внутри прямоугольника с центром симметрии в начале координат и сторонами 2a и 2b, параллельными координатным осям. Найти плотности распределения вероятностей величин X и Y и плотность распределения системы
распределена равномерно внутри прямоугольника с центром симметрии в начале координат и сторонами 2a и 2b, параллельными координатным осям. Найти плотности распределения вероятностей величин X и Y и плотность распределения системы  .
.
8. 21. Изделия некоторого производства подвергаются выборочному контролю. Каждое изделие может с вероятностью p оказаться годным и с вероятностью q – дефектным. В то же время изделие может быть проверено с вероятностью 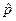 и не проверено с вероятностью
и не проверено с вероятностью 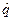 . Изделия выбираются до обнаружения первого дефектного изделия. Пусть X – число изделий, прошедших через стол контролера, из них Y – число дефектных, но не обнаруженных. Найти: а) совместное распределение (X, Y); б) распределения X и Y; в) M[X] и M[Y]; г) корреляционный момент R[X, Y].
. Изделия выбираются до обнаружения первого дефектного изделия. Пусть X – число изделий, прошедших через стол контролера, из них Y – число дефектных, но не обнаруженных. Найти: а) совместное распределение (X, Y); б) распределения X и Y; в) M[X] и M[Y]; г) корреляционный момент R[X, Y].
|
|
|
8. 22. Пусть случайные величины X, Y и  независимы и одинаково распределены. Найти вероятность того, что хотя бы одна из величин X и Y примет значение, большее каждой из величин
независимы и одинаково распределены. Найти вероятность того, что хотя бы одна из величин X и Y примет значение, большее каждой из величин  .
.
|
|
|




 X
X