 |
9. Законы распределения вероятностей функций от случайных величин
|
|
|
|
9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ ФУНКЦИЙ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Основные понятия раздела
Теория вероятностей в своей прикладной части связана, прежде всего, с решением следующей (типичной) задачи: по функции распределения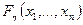 
системы случайных величин 
необходимо определить функцию распределения 
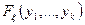системы случайных величин 
, если известны функциональные зависимости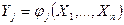 
; 
. При этом возможны следующие варианты задач: а) 
; б) 
; в) 
; г) 
– любое целое число.
Для непрерывных случайных величин задача а) формулируется следующим образом: по плотности распределения вероятностей 
случайной величины Х определить плотность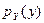 
случайной величины 
. Если функция 
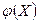является монотонной и дифференцируемой, то плотность величины Y определяется по формуле:
.
Если же функция 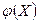такова, что обратная ей функция неоднозначна, т. е. одному значению аргумента y соответствует несколько значений функции 
, то в соответствии с теоремой сложения вероятностей несовместных событий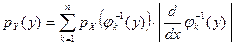 
.
Пусть система двух случайных величин 
является результатом функционального преобразования системы случайных величин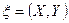 
(вариант 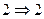). Предполагается, что прямое
и обратное
преобразования взаимно однозначны, непрерывны и дифференцируемы. Тогда, зная плотность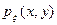 
системы ξ , можно найти плотность 
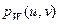системы W по формуле:
,
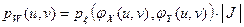где якобиан преобразования 
.
Если 
, то, в частности, при n=2
.
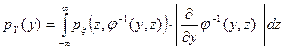Задачи с решениями
1. Случайная величина 
распределена по закону, заданному таблицей:
| X | -1 | ||
| P | 0, 2 | 0, 3 | 0, 5 |
Найти закон распределения вероятностей величины 
.
Решение. Для построения закона распределения найдем соответствующие вероятности:
|
|
|
;
.
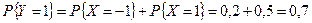Отсюда окончательно получаем:
| Y | ||
| P | 0, 3 | 0, 7 |
2. Случайная величина X распределена равномерно на интервале 
. Найти закон распределения вероятностей случайной величины 
.
Решение. Функция 
является монотонной на заданном интервале. Она имеет обратную функцию 
, следовательно, для нахождения закона распределения Y применима формула:
,
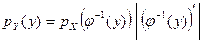где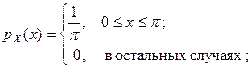 
и 
.
Окончательно имеем
3. Законы распределения числа очков, выбиваемых независимо каждым из двух стрелков, заданы таблицами:
| X | |||
| P | 0, 1 | 0, 3 | 0, 6 |
| Y | |||
| P | 0, 2 | 0, 3 | 0, 5 |
Найти закон распределения вероятностей суммы очков, выбиваемых двумя стрелками.
Решение. Новая случайная величина 
принимает значения: 2, 3, 4, 5, 6 с вероятностями:
Условие нормировки выполняется: 
.
4. Независимые случайные величины X и Y распределены нормально с параметрами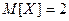 
, 
, 
, 
. Найти плотность распределения вероятностей и функцию распределения вероятностей их суммы.
Решение. Если известны плотности распределения вероятностей 
и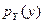 
независимых случайных величин X и Y, то плотность распределения их суммы записывается следующим образом:
.
Применив эту формулу для нашего случая, получим
.
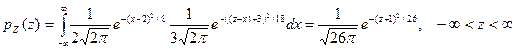Зная плотность, найдем функцию распределения вероятностей
.
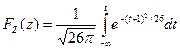5. Система случайных величин 
распределена нормально с плотностью распределения вероятностей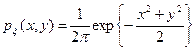 
. Найти плотность распределения вероятностей системы 
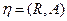, если 
, 
.
Решение. Для определения плотности распределения вероятностей системы 
применим формулу 
, где 
, 
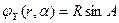есть обратное преобразование и 
– Якобиан обратного преобразования. Подставив в формулу плотности системы 
заданные преобразования и найденное значение Якобиана, получим:
.
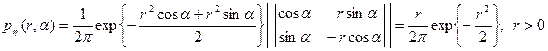6. Положение случайной точки 
равновероятно внутри квадрата со сторонами 1 и с центром в начале координат. Определить плотность распределения вероятностей случайной величины 
.
|
|
|
Решение. Для функции нескольких случайных аргументов удобнее решать задачу исходя из формулы функции распределения вероятностей. Рассмотрим отдельно два случая: а)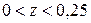 
и б)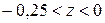 
(Рис. 9. 1, а), б)).
Функция распределения случайной величины Z в случае а) определяется следующим образом:
,
в случае б):
.
Дифференцируя эти выражения по z, получим плотность распределения вероятностей: а) 
, б) 
. Отсюда окончательно получаем:
7. Случайная величина X имеет нормальное распределение с параметрами 
. Определить плотность распределения вероятностей величины
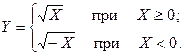
Решение. В рассматриваемом случае обратная функция неоднозначна, т. к. одному и тому же значению 
соответствуют два значения: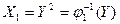 
, 
. Так как обратное преобразование двузначно, то плотность находится по формуле: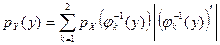 
. Отсюда получаем:
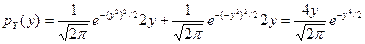при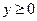 
.
В оставшихся случаях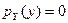 
.
 |
8. Случайные величины X и Y независимы и распределены по закону Пуассона: 
, 
, 
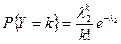. Найти закон распределения величины .
Решение. Для независимых случайных величин X и Y с дискретным распределением закон распределения их суммы находится по формуле:
,
где m есть сумма значений величин X и Y. Применим эту формулу для нашего случая:
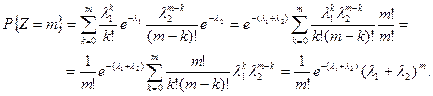
Таким образом, сумма независимых случайных величин, распределенных по закону Пуассона, также имеет распределение Пуассона.
9. Независимые случайные величины X и Y имеют показательное распределение с параметрам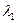и 
и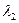 
соответственно. Найти плотность распределения вероятностей и математическое ожидание величины 
.
Решение. Закон распределения вероятностей частного двух независимых случайных величин в общем случае находится по формуле: 
. Введя обозначения для обратного преобразования: 
, 
, найдем Якобиан: 
. Определим плотность распределения
.
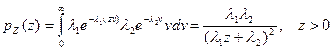Математическое ожидание величины Z есть
.
Интеграл в заданных пределах не существует, т. к. 
, следовательно, случайная величина Z не имеет математического ожидания.
10. Заданы плотности равномерно распределенных независимых случайных величин X и Y: 
в замкнутом интервале 
, вне этого интервала 
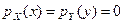. Найти плотность распределение вероятностей и дисперсию случайной величины 
.
Решение. Закон распределения вероятностей разности двух независимых случайных величин в общем случае задается формулой: 
. Имея в виду обратное преобразование 
и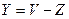 
, вычислим Якобиан: 
. Подставляя в общую формулу значение Якобиана и плотностей составляющих и учитывая, что значения величины Z изменяются в интервале 
(причем, т. к. 
при 
, а при 
, 
), получим
|
|
|
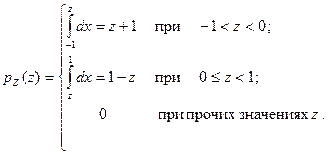
Таким образом, величина Z имеет известное распределение Симпсона. Дисперсия 
.
|
|
|
