 |
Задачи для самостоятельной работы
|
|
|
|
9. 1. Случайная величина X распределена равномерно на отрезке 
. Найти плотности распределения и функции распределения вероятностей величин 
и 
.
9. 2. Выработка двух бригад маляров, работающих независимо, характеризуется следующими данными:
| ||||
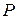
| ? | 0, 1 | 0, 1 | 0, 4 |
| ||||
|
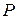
| 0, 4 | ? | 0, 1 | 0, 1 |
Составить закон распределения вероятностей суммарной выработки бригад маляров.
9. 3. Количество электроэнергии X, потребляемое первым предприятием, и количество электроэнергии Y, потребляемое вторым предприятием, заданы таблично:
|
| |||
|
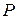
| 0, 2 | ? | 0, 6 |
|
| |||
|
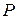
| ? | 0, 5 | 0, 1 |
Составить закон распределения количества энергии, потребляемой обоими предприятиями и найти математическое ожидание и дисперсию новой случайной величины.
9. 4. Пусть X и Y независимые случайные величины, имеющие одинаковое показательное распределение. Найти плотность распределения вероятностей и асимметрию случайной величины 
.
9. 5. Случайная величина X имеет геометрическое распределение. Найти функцию распределения случайной величины 
.
9. 6. Дискретная случайная величина X задана таблицей
|
| 
| 
| 
|
|
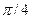
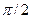
| 0, 2 | 0, 7 | 0, 1 |
Найти закон распределения вероятностей и дисперсию величины .
9. 7. Случайная величина X распределена по закону Коши. Найти плотность распределения вероятностей величин 
, 
, 
.
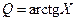9. 8. Найти закон распределения вероятностей суммы двух независимых случайных величин, распределенных по геометрическому закону.
9. 9. Случайные величины X и Y независимы и равномерно распределены на отрезке 
. Найти плотность распределения величины 
.
9. 10. Найти математическое ожидание и дисперсию произведения двух независимых случайных величин X и Y с равномерным законом распределения вероятностей: X – на отрезке 
и Y – на отрезке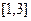 
.
|
|
|
9. 11. Задана плотность распределения случайной величины X
Найти плотность распределения вероятностей величины 
.
9. 12. Случайная величина X имеет нормальное распределение с параметрами 
. Найти плотность распределения случайной величины .
9. 13. Случайная величина X задана плотностью распределения вероятностей
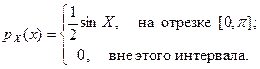
Найти плотность распределения вероятностей величин и 
.
9. 14. Найти распределение вероятностей суммы независимых случайных величин X и Y, заданных функциями распределения вероятностей: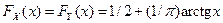 
.
9. 15. Дискретные независимые случайные величины X и Y заданы распределениями:
|
| ||
|
| 0, 3 | 0, 7 |
|
| ||
|
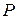
| 0, 6 | 0, 4 |
Найти распределение вероятностей величины 
.
9. 16. Независимые случайные величины X и Y заданы плотностями распределений: 
; 
. Найти плотность распределения вероятностей величины .
9. 17. Найти закон распределения вероятностей суммы случайных величин X и Y, имеющих следующее распределение:
.
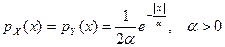9. 18. Плотности независимых случайных величин X и Y равны:
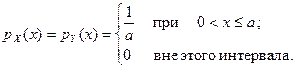
Найти плотность распределения вероятностей частного 
.
9. 19. Бросаются три игральные кости. Пусть X – сумма очков, выпадающих на их верхних гранях. Найти закон распределения вероятностей случайной величины X.
9. 20. Найти плотность распределения вероятностей модуля радиуса-вектора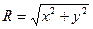 
, если случайные величины X и Y независимы и распределены по нормальному закону с параметрами 
, 
.
9. 21. Случайная величина X имеет плотность распределения вероятностей 
. Найти плотность величин Y=2X, когда –a< X< a, и Z=-2X, когда a< X< b.
9. 22. Случайная величина X распределена по закону
Найти функцию распределения вероятностей случайной величины 
.
9. 23. Случайная величина X имеет плотность
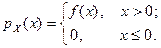
Найти законы распределения вероятностей величин 
, 
, 
.
|
|
|
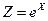9. 24. Случайная величина X распределена нормально с параметрами (a,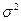 
). Доказать, что линейное преобразование Y=AX+B также распределено нормально.
9. 25. Найти плотность распределения вероятностей случайной величины Z=X/Y, если X и Y независимы и подчиняются закону распределения Рэлея с параметром 
.
9. 26. Найти функцию распределения вероятностей, математическое ожидание и дисперсию случайной величины Z=X+YX, где X и Y независимы, причем X имеет нормальное распределение с параметрами (0, 1), а Y – бинарная случайная величина с распределением P{Y=-1}=P{Y=1}=0, 5.
|
|
|
