Малатдегидрогеназа. 41. Расчет констант комплексообразования при взаимодействии двух субпопуляций антител с моновалентным антигеном.

Малатдегидрогеназа

 В гомогенном иммунофермент­ном анализе обычно используют малатдегидрогеназу из сердца свиньи. Молекула фермента состоит из двух идентичных субъеди­ниц с молекулярной массой по 35 000. Каждая из субъединиц имеет центр связывания молекулы кофермента NAD+ и обладает каталитической активностью при диссоциации молекулы на субъ­ единицы. Изоэлектрическая точка 6, 2. Молекула содержит 14 SH -групп, две из которых существенны для связывания субстрата в активном центре. Фермент достаточно стабилен и сохраняет активность в течение года при 4°С в виде суспензии под сульфа­ том аммония. Специфичность: Малатдегидрогеназа катализирует реакцию восстановления оксалоацетата до малата под действием NADH: оксалоацетат + NADH + Н+ L-малат + NAD+ Каталитическую активность измеряют по скорости уменьшения оптической плотности восстановленной формы NADH при длине волны 340 нм. Активаторами фермента являются фосфат, Zn2+, малат; ингибиторами — оксалоацетат, 8-оксихинолин, AMP, ADP, АТР, сульфит, тироксин, фенолы. Фотометрический способ определения ферментативной актив­ ности малатдегидрогеназы. В кювету спектрофотометра к 2, 58 мл 0, 1 М К-фосфатного буфера, pH 7, 4, добавляют 0, 2 мл 4, 5 мМ раствора оксалоацетата в том же буфере и 0, 2 мл 3 мМ раствора NADH. Кювету термостатируют и затем вносят 20 мкл раствора фермента (с концентрацией 1 мкг/мл) и регистрируют изменение оптической плотности раствора в течение 5 мин при длине волны 340 нм.

41. Расчет констант комплексообразования при взаимодействии двух субпопуляций антител с моновалентным антигеном.

Одним из простых приближений при описании реальных систем взаимодействия моновалентного антигена (гаптена) с антителами может быть модель, согласно которой набор популяций антител заменяется двумя – высокоаффинной и низкоаффинной, каждая из которых характеризуется собственной константой комплексообразования – К₁ и К₂.

Получаемая при анализе зависимости связывания неизвестной популяции антител с антигеном в координатах Скэтчарда вогнутая кривая может свидетельствовать о существовании двух фракций антител – высокоаффинной и низкоаффинной. Для определения четырех неизвестных параметров – К₁, К₂, [AT₁]₀ и [АТ₂]_о можно воспользоваться одним из следующих методов.

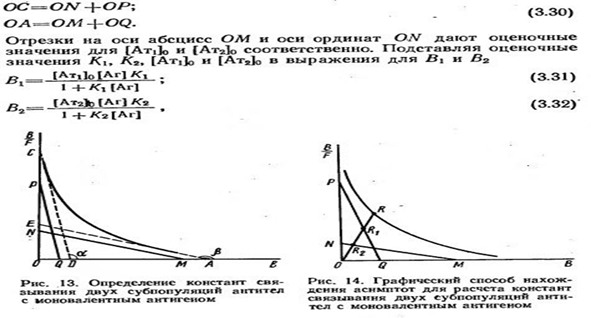
1. Параметры можно оценить по углам наклона асимптот гиперболы и отрезкам, отсекаемым ими на оси абсцисс и ординат ( рис. 13 ). Для построения асимптот используют следующий прием. По концевым участкам экспериментальной кривой проводят прямые (рис. 13 – пунктир), которые дают первоначальное приближение констант K₁ и К₂ (tgα ~K'₁; tgβ ~К’₂). Путем параллельного перемещения прямых подбирают такое их положение, чтобы сумма отрезков, отсекаемых ими на осях координат, была равна соответствующим отрезкам на тех же осях, отсекаемых самой кривой при экстраполяции ее к осям координат:

находят приближенные параметры В₁ и В₂ и В=В₁+В₂ при различных концентрациях Аг. С использованием полученных значений строят теоретическую зависимость B/F от В(символом B обозначают [АтАг], а F – [Аг]), сравнивают ее с экспериментальной и подбирают новые оценочные параметры до наилучшего совпадения теоретической и экспериментальной кривой.

2. Для нахождения асимптот гиперболы можно воспользоваться чисто графическим методом, заключающимся в построении двух прямых PQ и NM (рис. 14), для которых выполняется соотношение 

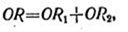
т. е. отрезок OR, соединяющий начало координат с любой точкой R, находящейся на гиперболе, равен сумме отрезков OR₁ и OR₂, соединяющих начало координат с точками пересечения отрезка OR с асимптотами.

3. Для оценки параметров К₁, К₂, [AT₁]₀ и [Ат₂]₀ часто используют следующий метод, основанный на анализе графической зависимости B/F от В. Из экспериментально полученной кривой связывания (рис. 13) путем экстраполяции находят точки пересечения кривой с осями абсцисс и ординат (А и С соответственно). Проводят касательные в этих точках к кривой до пересечения их с осями абсцисс и ординат в точках D и Е.