 |
Переходные процессы электропривода с учётом нелинейности механической характеристики.
|
|
|
|
Электродвигатели постоянного тока последовательного и смешанного возбуждения, а также асинхронные двигатели (АД) имеют нелинейные механические характеристики, но механическая характеристика АД при постоянных параметрах двигателя имеет известное аналитическое выражение в виде формулы Клосса:
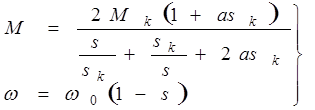, (1)
в то время как механические характеристики ДПТ ПВ и ДПТ СВ из-за отсутствия удовлетворительного аналитического описания кривой намагничивания не имеют подобных выражений. Поэтому для электроприводов с асинхронными двигателями найдены аналитические решения переходных процессов для случая постоянства статического момента. В целях упрощения важных выводов из аналитического рассмотрения переходных процессов с асинхронными двигателями примем статический момент равным нулю. Тогда, используя основное уравнение движения и выражение Клосса, получим уравнение в дифференциалах 
, (2)
левую и правую части которого можно проинтегрировать и найти
, (3)
где 
- постоянная интегрирования, определяемая из начальных условий: при 
, т.е.
, (4)
Как видно из (3), удобнее рассматривать время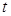 
как функцию скольжения 
. Поэтому, подставив (4.) в (3), получим зависимость времени переходного процесса от скольжения:
, (5)
до 
определяется из (5) при 
. В связи с тем, что это время является сложной функцией 
, из уравнения 
, (6) находим оптимальное критическое скольжение
, (7)
при котором время переходного процесса будет минимальным (Рис.1). При этом времени минимальными будут также потери энергии за время переходного процесса.
Если принять 
, то на основании упрощенной формулы Клосса
|
|
|
, (8)
можно определить средний электромагнитный момент АД за время переходного процесса
, (9)
который является сложной функцией критического скольжения 
. Исследование функции (4.) показывает, что наибольшее значение средний момент имеет при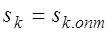 
.
Рассмотрим частные случаи переходных процессов вхолостую при :
а) Пуск вхолостую: 
,
При 
: 
При 
: 
,
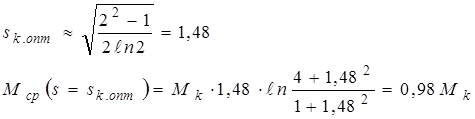
в) Реверс вхолостую: 
,
Из приведенных частных случаев следует, что при оптимальном критическом скольжении средний электромагнитный момент АД в переходном процессе вхолостую составляет 
, что и обеспечивает минимум времени переходного процесса. При скольжениях, отличных от оптимального, средний момент уменьшается.
Асинхронные двигатели общепромышленного применения имеют 
, что значительно меньше найденных оптимальных значений. Поэтому для нерегулируемых электроприводов с частыми пусками и торможениями (например, краново-металлургические механизмы, лифты) применяют асинхронные короткозамкнутые двигатели с повышенным скольжением, например, серий 4МТК, 4АС, имеющих критическое скольжение 
. Электроприводы с такими двигателями имеют меньшее время переходных процессов и меньшие потери энергии по сравнению с асинхронными короткозамкнутыми двигателями нормального исполнения.
Для частотно-регулируемых асинхронных электроприводов, где в переходном процессе формируется требуемый электромагнитный момент, лучшие энергетические показатели и меньшие потери энергии будут иметь асинхронные двигатели с малым критическим скольжением, т.е. серий 4А, 2АИР и т.п.
12. ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ ЭЛЕКТРОПРИВОДА С АСИНХРОННЫМ КОРОТКОЗАМКНУТЫМ ДВИГАТЕЛЕМ.
При прямом включении АД на сеть, сильное влияние на переходные процессы оказывают электромагнитные процессы.
При ωэл=0:
,
где Мп.уст.- установившееся значение пускового момента, которое определяется по формуле Клосса:
|
|
|
; 
; 
; 
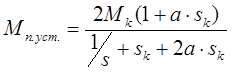
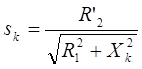α1,α2 - коэффициенты затухания: 
; 
; 
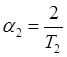
α1<<α2, поэтому характер изменения момента определяются главным образом переменными составляющими момента, затухающими с коэффициентом α1.
Логарифмический декремент затухания:
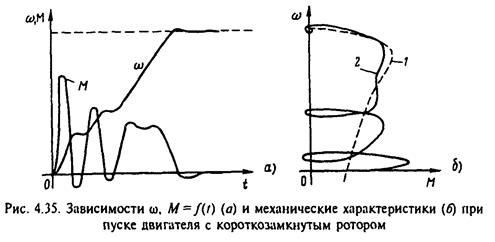
При разгоне АД:
При реверсе, при незатухшем магнитном потоке, Ммакс=(12…18)Мном. Для уменьшения, используются:
1.детерменированный пуск
2.система РН-АД
|
|
|
