Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М. : Проспект, 2008. – С.341–355.

VТема: Общие понятия о системах уравнений, используемых в эконометрике

1. Для системы одновременных уравнений
, где
– процентная ставка,
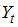– реальный ВВП,
– объем денежной массы,
– внутренние инвестиции,
– реальные государственные расходы,
эндогенными являются переменные …

 

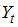
Решение
Эндогенными называются зависимые переменные, которые стоят в левых частях уравнений, число эндогенных переменных равно числу уравнений системы. В данном случае эндогенными являются , 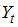и .

Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.

 

2. Установите соответствие между видом и классом эконометрических уравнений.
(1)

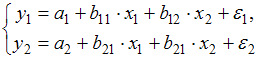
(2)

(3)

			система независимых уравнений
			система рекурсивных уравнений
			система одновременных уравнений
			система нормальных уравнений

Решение
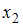В системе (1) в обоих уравнениях зависимые переменные и зависят только от независимых переменных и . Это система независимых уравнений.
В системе (2) второе уравнение содержит в правой части только независимые переменные и 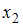, а первое уравнение для уже включает в себя и зависимую переменную , определенную во втором уравнении. Это система рекурсивных уравнений.
В системе (3) зависимые переменные и содержатся и в правой, и в левых частях уравнения. Это система одновременных уравнений.
Система нормальных уравнений не относится к классу эконометрических уравнений.

Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.

3. Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.

 

 

			зависимых
			эндогенных
			экзогенных
			независимых

Решение
Система эконометрических уравнений включает множество переменных, среди которых выделяют экзогенные и эндогенные переменные. В левой части системы эконометрических уравнений находятся только эндогенные (зависимые) переменные.

Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.

Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.

 

 

4. Установите соответствие между видом и классом системы эконометрических уравнений:

(1)

 

			система одновременных уравнений с лаговыми переменными
			система независимых уравнений
			система одновременных уравнений без лаговых переменных

Решение
Рассмотрим каждую из систем эконометрических уравнений.
В системе (1) в правой части первого уравнения стоит переменная S_t, которая во втором уравнении находится в левой части, следовательно, система является системой одновременных уравнений. Во втором уравнении системы (1) одновременно с переменной P_t находится лаговая переменная P_t-1, поэтому система (1) является системой одновременных уравнений с лаговыми переменными.
В системе (2) в левой части представлены переменные yt и wt, которые не входят в правую часть уравнений системы, поэтому система (2) является системой независимых уравнений.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.

 

 

5. При построении систем эконометрических уравнений различают три класса моделей:
(1) система независимых уравнений;
(2) система рекурсивных уравнений;
(3) система одновременных уравнений.
Отнесите предложенные модели к соответствующему классу.

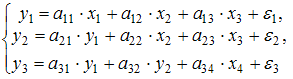
Решение
Модель, в которой – продуктивность коров, можно назвать моделью экономической эффективности сельскохозяйственного производства. Эта модель содержит в правой части только независимые переменные, поэтому она может быть отнесена к классу «система независимых уравнений».
Модель, в которой – производительность труда, может быть названа моделью производительности труда и фондоотдачи. Это модель содержит в первом уравнении только независимые переменные, а во втором уравнении в правой части встречается и зависимая переменная ; это значит, что модель можно отнести к классу «система рекурсивных уравнений».
Модель, в которой – темп изменения месячной заработной платы, может служить моделью динамики цены и заработной платы. В правых частях обоих уравнений содержатся зависимые переменные, поэтому данная модель может быть отнесена к классу «система одновременных уравнений».
Система, в которой y – объем производства, вообще не является какой бы то ни было системой эконометрических уравнений – это система нормальных уравнений для определения параметров парной линейной регрессии.

Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.

6. Модель равенства спроса и предложения, в которой предложение является линейной функцией цены p, а спрос 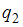является линейной функцией цены p и дохода y, состоит из уравнений …

 

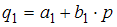
Решение
В модели предложение является линейной функцией цены p. Значит, уравнение для предложения будет иметь вид 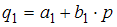. Спрос 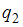является линейной функцией цены p и дохода y, значит, уравнение для спроса 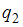будет иметь вид . Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим: .
Модель будет иметь вид

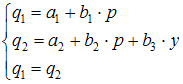
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.

 

 

7. Системой эконометрических уравнений не является система линейных _____ уравнений.

 

			нормальных
			стандартизованных
			рекурсивных
			одновременных

Решение
Система линейных одновременных уравнений является одним из видов систем эконометрических уравнений.
Система рекурсивных уравнений также является видом системы эконометрических уравнений.
Система нормальных уравнений используется при расчете оценок параметров линейных моделей с помощью МНК и не является системой эконометрических уравнений (правильный вариант ответа).
Стандартизованное уравнение регрессии используется при моделировании линейных уравнений множественной регрессии для расчета стандартизованных коэффициентов регрессии и ранжировании факторов по силе связи с зависимой переменной и не является системой эконометрических уравнений (правильный вариант ответа).

Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.

Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.

 

8. Установите соответствие между классом и видом системы эконометрических уравнений:
(1) система одновременных уравнений
(2) система рекурсивных уравнений
(3) система независимых уравнений

Решение
Рассмотрим каждую из систем эконометрических уравнений.
(3) – система независимых уравнений. В такой системе в правой части уравнений стоят только независимые переменные, которые не могут находиться в левой части других уравнений системы. Поэтому для системы (3) правильным вариантом ответа является система

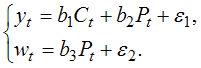
(1) – система одновременных (взаимозависимых) уравнений. В правой части уравнений такой системы одновременно с независимыми переменными стоят и зависимые переменные, которые в других уравнениях находятся в левой части и являются функциями набора зависимых и/или независимых переменных. Порядок следования зависимых переменных y в правой части уравнений не зависит от количества предыдущих уравнений. Поэтому для системы (1) правильным вариантом ответа является система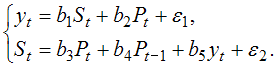
(2) является системой рекурсивных уравнений. В такой системе в правой части уравнений стоят как зависимые, так и независимые переменные; при этом каждое последующее уравнение в правой части включает зависимые переменные y только предыдущих уравнений системы. Поэтому для системы (2) правильным вариантом ответа является система
Система содержит ошибку, так как в левой части всех уравнений системы стоит переменная у_t. Поэтому данная система не может быть отнесена ни к одному из классов систем эконометрических уравнений.

Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–345.

Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–233.

 

 

9. Модель равенства спроса и предложения, где предложение и спрос 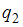являются линейными функциями цены p, состоит из уравнений …

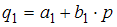
Решение
В модели предложение и спрос 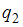являются линейными функциями цены p. Значит, уравнение для предложения будет иметь вид 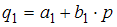, а уравнение для спроса 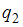– . Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим: .
Модель будет иметь вид
,

Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.

 

 

10. Изучаются модели зависимости спроса и предложения 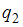от цены p и прочих факторов. Установите соответствие между видом и классом эконометрических уравнений.
(1)
(2)
(3)

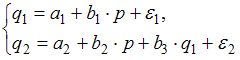
			система независимых уравнений
			система одновременных уравнений
			система рекурсивных уравнений
			система приведенных уравнений

Решение
В системе (1) оба уравнения зависят только от независимой переменной p. Это система независимых уравнений, и мы не предполагаем, что спрос и предложение 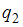связаны между собой.
В системе (2) зависимые переменные спрос и предложение 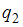содержатся и в правой, и в левой частях уравнения. Это система одновременных уравнений.
В системе (3) первое уравнение содержит в правой части только независимую переменную p, а второе уравнение уже включает в себя и зависимую переменную , определенную в первом уравнении. Это система рекурсивных уравнений.
Система приведенных уравнений не является классом систем одновременных уравнений.
Эконометрика: учеб. / под ред. Д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.

 

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: