Тема: Проверка статистической значимости эконометрической модели

1. Для регрессионной модели известны следующие величины дисперсий:
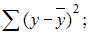
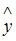где y – значение зависимой переменной по исходным данным; – значение зависимой переменной, вычисленное по регрессионной модели; – среднее значение зависимой переменной, определенное по исходным статистическим данным. Для указанных дисперсий справедливо равенство …

Решение
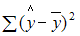Назовем приведенные дисперсии: – общая дисперсия; – объясненная дисперсия; 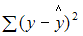– остаточная дисперсия. При анализе статистической модели величину общей дисперсии рассматривают как сумму объясненной и остаточной дисперсий, поэтому справедливо равенство: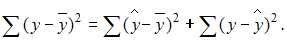

Эконометрика: учеб. / И. И. Елисеева [и др.]; под ред. И. И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 63-64.

2. Если известно уравнение множественной регрессии построенное по результатам 50 наблюдений, для которого общая сумма квадратов отклонений равна 153, и остаточная сумма квадратов отклонений равна 3, то значение F-статистики равно …

			766,67
			877,45

Решение
Расчет F -статистики начинается с разложения общей суммы квадратов отклонений на сумму квадратов отклонений, объясненную регрессией, и остаточную сумму квадратов отклонений:
, где
– общая сумма квадратов отклонений
– сумма квадратов отклонений, объясненная регрессией
– остаточная сумма квадратов отклонений
В нашем случае дано , . Следовательно,
Существует равенство между числом степеней свободы общей, факторной и остаточной сумм квадратов отклонений:
n – 1 = m + (n – m – 1 ), где n –число наблюдений, m – число параметров перед переменными в уравнений регрессии.
Число степеней свободы для общей суммы квадратов отклонений равно n – 1. В нашем случае n – 1 = 49.
Число степеней свободы для остаточной суммы квадратов отклонений равно n – m – 1 = 46.
Число степеней свободы для факторной суммы квадратов отклонений равно m = 3.
Рассчитаем факторную и остаточную дисперсии на одну степень свободы по формулам

F -статистика вычисляется по формуле
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 155.

3. По результатам 50 статистических наблюдений построено уравнение множественной регрессии Число степеней свободы остаточной суммы квадратов отклонений для этого уравнения равно …

Решение
Число степеней свободы для остаточной регрессии может быть определено по формуле (n – m – 1), где n – число наблюдений, m – число параметров перед переменными в уравнении множественной регрессии. Значит в нашем случае число степеней свободы для остаточной регрессии равно 50 – 3 –1= 46.

Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. C. 67–70.

4. При расчете скорректированного коэффициента множественной детерминации пользуются формулой , где …

			n – число наблюдений; m – число факторов, включенных в модель множественной регрессии
			m – число наблюдений; n – число факторов, включенных в модель множественной регрессии
			n – число параметров при независимых переменных; m – число факторов, включенных в модель множественной регрессии
			n – число параметров при независимых переменных; m – число наблюдений

Решение
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и имеет вид , где n – число наблюдений, m – число факторов, включенных в модель множественной регрессии.

Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. C. 67–70.