Тема: Оценка значимости параметров эконометрической модели

1. Проверка статистически значимого отличия от нуля оценок коэффициентов линейной модели

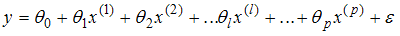
осуществляется путем последовательного сравнения отношений ( –среднеквадратическая ошибка параметра ) с точкой, имеющей распределение …

			Стьюдента
			Фишера
			Дарбина – Уотсона
			нормальное

Решение
При проверке статистически значимого отличия от нуля оценок коэффициентов линейной регрессионной модели 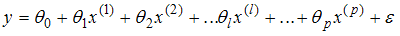выдвигается гипотеза о нулевом значении оценки параметра. Для каждого коэффициента регрессии модели рассчитывают отношение его среднеквадратической ошибки к значению оценки . Полученное значение отношения последовательно сравнивается с точкой, имеющей распределение Стьюдента.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 73.

2.Для уравнения множественной регрессии вида на основании 14 наблюдений рассчитаны оценки параметров и записана модель: (в скобках указаны значения t -статистики соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости

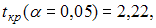
Для данного уравнения при уровне значимости

Решение
Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии формулируется нулевая гипотеза при альтернативной гипотезе 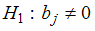. Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если 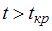, коэффициент значим; если коэффициент незначим. В нашем случае при уровне значимости 0,05 значимыми является параметры
Эконометрика. Под ред. Елисеевой И.И., М.: Финансы и статистика, 2005. С.160–165.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. – М.: ЮНИТИ, 2002. – С.40–52.

3.Для уравнения множественной регрессии вида на основании 14 наблюдений рассчитаны оценки параметров и записана модель: 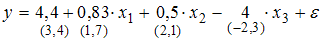(в скобках указаны значения t -статистики, соответствующие параметрам регрессии). Известны критические значения Стьюдента для различных уровней значимости

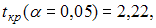
При уровне значимости 0,1 значимыми являются параметры …

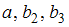
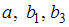
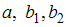
Решение
Чтобы оценить значимость параметров регрессии используется t -критерий Стьюдента. Для каждого коэффициента регрессии формулируется нулевая гипотеза при альтернативной гипотезе Затем рассчитывается фактическое значение t -статистики, которое сравнивается с критическим значением Стьюдента для требуемого числа степеней свободы и уровня значимости. Если 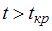, коэффициент значим; если коэффициент незначим. В нашем случае при уровне значимости 0,1 значимым является параметры
Эконометрика. Под ред. Елисеевой И.И., М.: Финансы и статистика, 2005. С.160–165.
Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. – М.: ЮНИТИ, 2002. – С.40–52.

4. Для уравнения множественной регрессии вида на основании 14 наблюдений рассчитаны оценки параметров и записана модель:

(в скобках указаны значения t -статистик, соответствующие параметрам регрессии). Известны критические значения Стьюдента при различных уровнях значимости

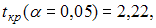
Для данного уравнения при уровне значимости

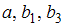
Решение
В нашем случае при уровне значимости 0,01 значимым является только параметр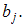

Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 160–170.

Кремер, Н.Ш. Эконометрика: учеб. для студентов вузов / Н. Ш. Кремер, Б. А. Путко; ред. Н. Ш. Кремер. – М.: ЮНИТИ, 2002. – С.40–52.

5. Если для среднеквадратической ошибки параметра и значения оценки этого параметра линейной эконометрической модели выполняется соотношение 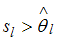, то это свидетельствует о статистической ______ параметра.

			ненадежности оценки
			надежности оценки
			ненадежности среднеквадратической ошибки
			надежности среднеквадратической ошибки

Решение
Превышение среднеквадратической ошибки параметра над значением его оценки свидетельствует о статистической ненадежности параметра.

Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 67.