Тема: Структура временного ряда

1. Автокорреляцией уровней ряда называется корреляционная зависимость между …

			последовательными уровнями ряда
			уровнями двух рядов
			компонентами, образующими уровни ряда
			факторами, формирующими уровень ряда

Решение
Автокорреляцией уровней ряда называется корреляционная зависимость между последовательными уровнями ряда.

Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 298.

2. Значение коэффициента автокорреляции второго порядка равно (-0,6), следовательно, ряд содержит …

			тенденцию
			убывающую тенденцию
			затухающую сезонную волну периодичностью 2 момента времени
			полиномиальную тенденцию с точкой минимума

Решение
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка коэффициента автокорреляции. Если временной ряд содержит тенденцию, то наиболее высокое (максимальное или чуть меньше, чем максимальное) значение наблюдается у коэффициента автокорреляции первого и/или второго порядка. Однако, по знаку коэффициента автокорреляции нельзя делать вывод о направленности тенденции. Поэтому вариант «ряд содержит убывающую тенденцию» является ошибочным, так как ряд при данном значении коэффициента автокорреляции может содержать и положительную тенденцию. Правильный вариант – «ряд содержит тенденцию».

Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 132–138.

3Дана автокорреляционная функция временного ряда

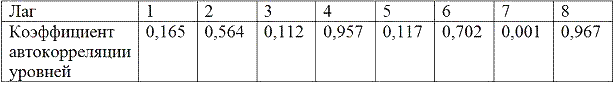
Верным будет утверждение, что ряд …

			имеет выраженную сезонную компоненту с лагом 4
			содержит только тенденцию, и не содержит сезонной компоненты
			имеет выраженную сезонную компоненту с лагом 6
			не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту

Решение
Высокое значение коэффициентов автокорреляции четвертого и кратного ему восьмого уровней позволяет сделать вывод, что ряд имеет выраженную сезонную компоненты, периодичность которой равна четырем.
Низкое значение коэффициента автокорреляции первого порядка позволяет предположить, что ряд не содержит трендовой компоненты.

Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. С. 132–137.

4. Значение коэффициента автокорреляции первого порядка характеризует …

			тесноту линейной связи
			качество модели временного ряда
			тесноту нелинейной связи
			значимость тренда

Решение
Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков коэффициента автокорреляции. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка, а само значение коэффициента корреляции рассчитывается по аналогии с парным коэффициентом линейной корреляции и характеризует тесноту линейной связи между двумя переменными. Поэтому варианты «качество модели временного ряда», «тесноту нелинейной связи» и «значимость тренда» являются неверными.

Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 132–133.

5. Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …

			первого, второго, третьего и последующих порядков
			между трендовой, сезонной и случайной компонентами
			между несколькими временными рядами
			факторов, формирующих уровень ряда

Решение
Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции первого, второго и последующих порядков.

Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 302.