 |
Тема: Фиктивные переменные
|
|
|
|
1. В эконометрике фиктивной переменной принято считать …

| переменную, принимающую значения 0 и 1 | ||

| описывающую количественным образом качественный признак | ||
| переменную, которая может равняться только целому числу | |||
| несущественную переменную |
Решение
Качественное различие признаков можно формализовать с помощью любой переменной, принимающей два значения, не обязательно 0 или 1. Однако в эконометрической практике почти всегда используются фиктивные переменные типа «0-1», поскольку в этом случае можно интерпретировать результаты моделирования.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. С.190–195.
2. При исследовании зависимости потребления мяса от уровня дохода и пола потребителя можно рекомендовать …

| использовать фиктивную переменную – пол потребителя | ||

| разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола | ||
| использовать фиктивную переменную – уровень дохода | |||
| исключить из рассмотрения пол потребителя, так как данный фактор нельзя измерить количественным образом |
Решение
При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Они отражают неоднородность исследуемой статистической совокупности и используются для более качественного моделирования зависимостей в таких неоднородных объектах наблюдения. При моделировании отдельных зависимостей по неоднородным данным можно также воспользоваться способом разделения всей совокупности неоднородных данных на несколько отдельных совокупностей, количество которых равно количеству состояний dummy-переменной. Таким образом правильными вариантами ответов являются: «использовать фиктивную переменную – пол потребителя» и «разделить совокупность на две: для потребителей женского пола и для потребителей мужского пола».
|
|
|
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 121–127.
3. Дана таблица исходных данных для построения эконометрической регрессионной модели:

Фиктивными переменными не являются …

| стаж работы | ||

| производительность труда | ||
| уровень образования | |||
| уровень квалификации работника |
Решение
При построении регрессионной модели может возникнуть ситуация, когда необходимо включить в уравнение помимо количественных переменных переменные, отражающие некоторые атрибутивные признаки (пол, образование, регион и т.п.). Такого рода качественные переменные называются «фиктивными» (dummy) переменными. Для построения указанной в постановке задания модели используются фиктивные переменные: уровень образования и уровень квалификации работника. Остальные переменные не являются фиктивными, из предложенных вариантов это стаж работы и производительность труда.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 158–166.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 121–127.
4. Изучается зависимость цены квартиры (у) от ее жилой площади (х) и типа дома. В модель включены фиктивные переменные, отражающие рассматриваемые типы домов: монолитный, панельный, кирпичный. Получено уравнение регрессии:  ,
,
где  ,
, 
Частными уравнениями регрессии для кирпичного и монолитного являются …
|
|
|

|  для типа дома кирпичный для типа дома кирпичный
| ||

| 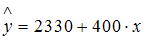 для типа дома монолитный для типа дома монолитный
| ||
 для типа дома кирпичный для типа дома кирпичный
| |||
 для типа дома монолитный для типа дома монолитный
|
Решение
Требуется узнать частное уравнение регрессии для кирпичного и монолитного домов. Для кирпичного дома значения фиктивных переменных следующие 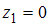 ,
,  . Уравнение примет вид:
. Уравнение примет вид: 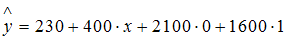 или
или  для типа дома кирпичный.
для типа дома кирпичный.
Для монолитного дома значения фиктивных переменных следующие  ,
,  . Уравнение примет вид
. Уравнение примет вид 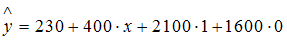
или 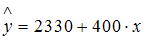 для типа дома монолитный.
для типа дома монолитный.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 167–182.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. С.190–195.
5. При анализе промышленных предприятий в трех регионах (Республика Марий Эл, Республика Чувашия, Республика Татарстан) были построены три частных уравнения регрессии:
 для Республики Марий Эл;
для Республики Марий Эл;
 для Республики Чувашия;
для Республики Чувашия;
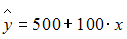 для Республики Татарстан.
для Республики Татарстан.
Укажите вид фиктивных переменных и уравнение с фиктивными переменными, обобщающее три частных уравнения регрессии.

| 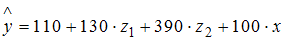
| ||

|  
| ||
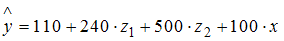
| |||
 
|
Решение
Три уравнения отличаются только свободным членом. Нужно ввести две фиктивные переменные, например 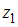 и
и  . Поскольку для Республики Марий значение свободного члена минимальное, то для нее
. Поскольку для Республики Марий значение свободного члена минимальное, то для нее 
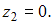
Пусть 
Тогда уравнение для Республики Чувашия можно переписать в виде
 или
или 
Пусть 
Тогда уравнение для Республики Татарстан можно переписать в виде  или
или 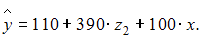
Итоговое уравнение будет 
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 167–182.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. С.190–195.
|
|
|
Тема: Спецификация эконометрической модели
1. Для регрессионной модели вида  необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.

| |||
Решение
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
2. В модели вида 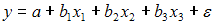 количество объясняющих переменных равно …
количество объясняющих переменных равно …

| |||
Решение
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения  , где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);  – случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
– случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 42–49.
Магнус, Ян Р. Эконометрика: начальный курс: Учебник для студ-ов вузов, обуч. по экон. спец. / Я.Р. Магнус, П.К. Катышев, А.А. Пересецкий; Акад. народ. хоз-ва при Правительстве Рос. Федерации. – М.: Дело, 2000. – С. 33.
3. При идентификации модели множественной регрессии  количество оцениваемых параметров равно …
количество оцениваемых параметров равно …

| |||
Решение
При оценке модели множественной регрессии  рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
|
|
|
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 40–50.
4. Ошибки спецификации эконометрической модели имеют место вследствие …

| неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора | ||
| недостоверности или недостаточности исходной информации | |||
| неоднородности данных в исходной статистической совокупности | |||
| недостаточного количества данных |
Решение
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для  . Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для
. Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для  , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
, но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 45.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 20–30.
Тема: Линеаризация нелинейных моделей регрессии
1. Для преобразования внутренне нелинейной функции  может быть применен метод …
может быть применен метод …

| разложения функции в ряд Тейлора | ||
| замены переменных | |||
| логарифмирования | |||
| потенцирования |
Решение
Функция  является внутренне нелинейной, и для нее отсутствует прямое преобразование, которое превратит ее в линейную функцию. Только разложением функции в ряд Тейлора, то есть заменой данной функции суммой полиномов, можно привести данную функцию к линейному виду.
является внутренне нелинейной, и для нее отсутствует прямое преобразование, которое превратит ее в линейную функцию. Только разложением функции в ряд Тейлора, то есть заменой данной функции суммой полиномов, можно привести данную функцию к линейному виду.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
2. Для линеаризации нелинейной функции  может быть применен метод …
может быть применен метод …

| логарифмирования и замены переменных | ||
| разложения функции в ряд Тейлора | |||
| потенцирования и замены переменных | |||
| обращения и замены переменных |
Решение
Функция 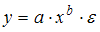 является внутренне линейной и с помощью логарифмирования может быть преобразована к виду
является внутренне линейной и с помощью логарифмирования может быть преобразована к виду  , которая является линейной относительно логарифмов переменных. Сделав замену переменных
, которая является линейной относительно логарифмов переменных. Сделав замену переменных  ,
, 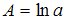 ,
, 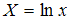 ,
,  , получим линейную функцию
, получим линейную функцию  . Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
. Поэтому для линеаризации используется сначала логарифмирование, затем замена переменных.
|
|
|
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
3 Для линеаризации нелинейной регрессионной модели 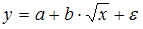 используется замена …
используется замена …

| 
| ||
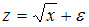
| |||
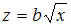
| |||

|
Решение
Линеаризация – процедура приведения нелинейной регрессионной модели к линейному виду путем различных математических преобразований. Это необходимо для обеспечения возможности использования метода наименьших квадратов, позволяющего оценить параметры линейных уравнений регрессии. В качестве одного из способов линеаризации используется замена переменных. Уравнение 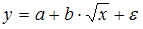 может быть линеаризовано заменой
может быть линеаризовано заменой  , в результате получаем модель линейного уравнения парной регрессии
, в результате получаем модель линейного уравнения парной регрессии 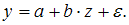
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 85.
4. Для линеаризации нелинейной функции 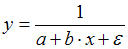 может быть применен метод ______ и замены переменных.
может быть применен метод ______ и замены переменных.

| обращения | ||
| потенцирования | |||
| логарифмирования | |||
| разложения функции в ряд Тейлора |
Решение
Обратив обе части равенства, получим линейную форму для переменной 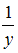 :
:  . Коэффициенты данной модели могут быть найдены стандартным методом наименьших квадратов.
. Коэффициенты данной модели могут быть найдены стандартным методом наименьших квадратов.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 96–99.
Бывшев В.А. Эконометрика: учеб. пособие / В.А. Бывшев. – М.: Финансы и статистика, 2008. – С.331–346.
Начало формы
|
|
|


