 |
Тема: Идентификация систем эконометрических уравнений
|
|
|
|
1. Установите соответствие между структурной формой модели и приведенной формой модели
(1) 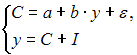
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах
(2) 
где R – процентная ставка,
Y – ВВП,
M – денежная масса,
I – инвестиции
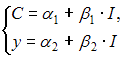 где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах
| |||
 где R – процентная ставка, Y – ВВП, M – денежная масса, I – инвестиции где R – процентная ставка, Y – ВВП, M – денежная масса, I – инвестиции
| |||
 где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах где C – личное потребление в постоянных ценах, y – национальный доход в постоянных ценах, I – инвестиции в постоянных ценах
|
Решение
Для модели Кейнса, которой является система (1), экзогенной переменной будет только переменная I (инвестиции). Поэтому приведенная форма модели имеет следующий вид: 
Неправильный вариант ответа для этой модели 
В этом случае перепутаны эндогенные и экзогенные переменные.
Для модели денежного рынка, которой является система (2), экзогенными переменными будут M (объем денежной массы) и I (инвестиции). Поэтому правильный вариант ответа для системы (2) – 
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
2. Дана структурная форма модели системы одновременных уравнений: 
Установите соответствие между обозначением и его наименованием:
(1) 
(2) 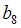
(3) 
| эндогенная переменная | |||
| структурный коэффициент | |||
| лаговая переменная | |||
| экзогенная переменная |
Решение
Рассмотрим каждое из обозначений.
(1) 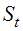 – эндогенная переменная системы, входит в левую часть второго уравнения.
– эндогенная переменная системы, входит в левую часть второго уравнения.
(2)  – структурный коэффициент, или коэффициент структурной формы модели.
– структурный коэффициент, или коэффициент структурной формы модели.
(3)  – лаговая переменная, характеризующая значение переменной
– лаговая переменная, характеризующая значение переменной  в предыдущий период.
в предыдущий период.
Вариант ответа «экзогенная переменная» характеризует независимую переменную системы, которая может входить только в правую часть уравнений системы. Этот вариант не является наименованием ни одного из обозначений.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–347.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–237.
|
|
|
3. Дана система одновременных эконометрических уравнений:

Система является точно идентифицируемой. Определите последовательность этапов алгоритма оценки ее параметров.
преобразование структурной формы модели в приведенную форму вида 
| |||
оценивание параметров приведенной формы модели (приведенных коэффициентов) 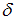 для каждого уравнения приведенной формы модели обычным МНК оцениваются для каждого уравнения приведенной формы модели обычным МНК оцениваются
| |||
трансформация коэффициентов приведенной формы модели в параметры структурной формы модели  и и 
| |||
| подстановка найденных значений коэффициентов в структурную форму системы эконометрических уравнений |
Решение
В случае точно идентифицируемой структурной формы модели для оценки ее параметров применяют косвенный метод наименьших квадратов (КМНК). При этом соблюдают следующую последовательность этапов КМНК:
1) структурная форма модели преобразовывается в приведенную форму модели; так как в системе 4 экзогенных переменных – (х1, х2, х3 и х4),то у правой части приведенной формы модели записывается сумма четырех произведений соответствующих коэффициентов приведенной формы и экзогенных переменных; для данной системы приведенная форма будет иметь вид

2) для каждого уравнения приведенной формы модели обычным МНК оцениваются параметры приведенной формы модели – приведенные коэффициенты 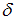 ;
;
3) коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели  и
и  ;
;
4) найденные значения коэффициентов подставляются в структурную форму системы эконометрических уравнений.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 265–266.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 347–353.
|
|
|
4. Дана структурная форма модели системы одновременных уравнений: 
Установите соответствие между обозначением и его наименованием:
(1) 
(2) 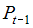
(3) 
| ошибка модели | |||
| лаговая переменная | |||
| эндогенная переменная | |||
| структурный коэффициент |
Решение
Рассмотрим каждое из обозначений.
(1)  – ошибка модели, учитывает влияние факторов случайного характера на зависимую переменную первого уравнения.
– ошибка модели, учитывает влияние факторов случайного характера на зависимую переменную первого уравнения.
(2) 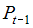 – лаговая переменная, характеризующая значение переменной
– лаговая переменная, характеризующая значение переменной 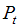 в предыдущий период.
в предыдущий период.
(3)  – зависимая переменная, то есть эндогенная переменная, входящая в левую часть первого уравнения системы.
– зависимая переменная, то есть эндогенная переменная, входящая в левую часть первого уравнения системы.
Вариант ответа «структурный коэффициент» не является наименованием ни одного из обозначений; структурными коэффициентами в данной системе являются коэффициенты  .
.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–347.
5. Модель мультипликатора-акселератора Кейнса
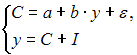
где C – личное потребление в постоянных ценах,
y – национальный доход в постоянных ценах,
I – инвестиции в постоянных ценах,
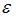 – случайная составляющая,
– случайная составляющая,
Установите соответствие:
(1) эндогенная переменная
(2) экзогенные переменная.
| y – национальный доход в постоянных ценах | |||
| I – инвестиции в постоянных ценах | |||
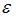 – случайная составляющая – случайная составляющая
|
Решение
В модели мультипликатора-акселератора Кейнса эндогенными переменные являются переменные C (личное потребление в постоянных ценах) и y (национальный доход в постоянных ценах). А экзогенными переменными является только переменная I (инвестиции в постоянных ценах). И 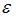 является случайной составляющей.
является случайной составляющей.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С.341–355.
|
|
|
6. Дана приведенная форма модели системы одновременных уравнений: 
Установите соответствие между обозначением и его наименованием:
(1) 
(2) 
(3) 
| эндогенная переменная | |||
| экзогенная переменная системы | |||
| приведенный коэффициент | |||
| структурный коэффициент |
Решение
Рассмотрим каждое из обозначений.
(1)  – эндогенная переменная системы, входит в левую часть первого уравнения.
– эндогенная переменная системы, входит в левую часть первого уравнения.
(2)  – независимая переменная, то есть экзогенная переменная системы, входит в правую часть уравнений приведенной формы системы.
– независимая переменная, то есть экзогенная переменная системы, входит в правую часть уравнений приведенной формы системы.
(3)  – приведенный коэффициент (коэффициент приведенной формы модели), являющийся нелинейной комбинацией структурных коэффициентов (коэффициентов структурной формы модели).
– приведенный коэффициент (коэффициент приведенной формы модели), являющийся нелинейной комбинацией структурных коэффициентов (коэффициентов структурной формы модели).
Вариант ответа «структурный коэффициент» не является наименованием ни одного из обозначений; кроме этого, структурные коэффициенты содержатся в структурной форме модели, а в задании рассматривается приведенная форма модели.
Эконометрика: учеб. / под ред. д-ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2008. – С. 341–347.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 230–237.
Тема: Отбор факторов, включаемых в модель множественной регрессии
1. При моделировании линейного уравнения множественной регрессии вида 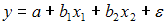 необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …

| x1 и x2 | ||
| y и { x1; x2 } | |||
| a и { b1; b2 } | |||
| b1 и b2 |
Решение
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения  , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);  – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
– случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 110–119.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 35–41.
Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2-е изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ-ДАНА, 2001. – С. 74–89.
Порядина, О.В. Эконометрическое моделирование линейных уравнений регрессии: учеб. пособие для студентов специальностей 061800 "Мат. методы в экономике" и 351400 "Прикладная информатика (в экономике)" / О. В. Порядина. – Йошкар-Ола: МарГТУ, 2005. – С. 22–26.
|
|
|
2. В модели множественной регрессии  определитель матрицы парных коэффициентов корреляции между факторами
определитель матрицы парных коэффициентов корреляции между факторами  ,
, 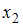 и
и  близок к нулю. Это означает, что факторы
близок к нулю. Это означает, что факторы  ,
, 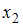 и
и  …
…

| мультиколлинеарны | ||
| независимы | |||
| количественно измеримы | |||
| значимы |
Решение
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы  были бы равны нулю.
были бы равны нулю.
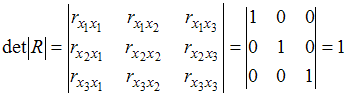 , поскольку
, поскольку  =
=  =
= 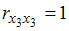 и
и  =
=  =
=  =0.
=0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
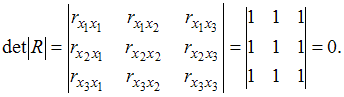
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 111–117.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. – С. 98–100.
3. Дана матрица парных коэффициентов корреляции.

Коллинеарными являются факторы …

|  и и 
| ||
 и и 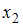
| |||
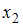 и и 
| |||
 и y и y
|
Решение
Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если  . В нашей модели только коэффициент парной линейной регрессии между факторами
. В нашей модели только коэффициент парной линейной регрессии между факторами  и
и  больше 0,7.
больше 0,7.  , значит, факторы
, значит, факторы  и
и  коллинеарны.
коллинеарны.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 113.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. – С. 98–100.
|
|
|
4. Для эконометрической модели линейного уравнения множественной регрессии вида  построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4) – независимые переменные):
построена матрица парных коэффициентов линейной корреляции (y – зависимая переменная; х(1), х(2), х(3), x(4) – независимые переменные):

Коллинеарными (тесно связанными) независимыми (объясняющими) переменными не являются …

| x(2) и x(3) | ||
| x(1) и x(3) | |||
| x(1) и x(4) | |||
| x(2) и x(4) |
Решение
При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. При этом осуществляют проверку коэффициентов линейной корреляции для каждой пары независимых (объясняющих) переменных. Эти значения отражены в матрице парных коэффициентов линейной корреляции. Считается, что наличие значений коэффициентов парной корреляции между объясняющими переменными, превышающих по абсолютной величине 0,7, отражает тесную связь между этими переменными (теснота связи с переменной y в данном случае не рассматривается). Такие независимые переменные называются коллинеарными. Если значение коэффициента парной корреляции между объясняющими переменными не превышает по абсолютной величине 0,7, то такие объясняющие переменные не являются коллинеарными. Рассмотрим значения парных коэффициентов межфакторной корреляции: между x(1) и x(2) значение равно 0,45; между x(1) и x(3) – равно 0,82; между x(1) и x(4) – равно 0,94; между x(2) и x(3) – равно 0,3; между x(2) и x(4) – равно 0,7; между x(3) и x(4) – равно 0,12. Таким образом, не превышают 0,7 значения  ,
,  ,
,  .
.
Следовательно, коллинеарными не являются факторы x(1) и x(2), x(2) и x(3), x(3) и x(4). Из последних перечисленных пар в вариантах ответов присутствует пара x(2) и x(3) – это верный вариант ответа. Для остальных пар: x(1 и x(3), x(1) и x(4), x(2) и x(4) – значения парных коэффициентов межфакторной корреляции превышают 0,7, и эти факторы являются коллинеарными.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 110–119.
Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2009. – С. 35–41.
5. В модели множественной регрессии  определитель матрицы парных коэффициентов корреляции между факторами
определитель матрицы парных коэффициентов корреляции между факторами  ,
, 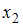 и
и  близок к единице. Это означает, что факторы
близок к единице. Это означает, что факторы  ,
, 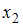 и
и  …
…

| независимы | ||
| мультиколлинеарны | |||
| количественно измеримы | |||
| значимы |
Решение
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы  были бы равны нулю.
были бы равны нулю.
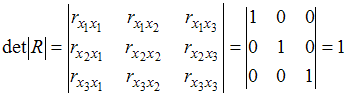 , поскольку
, поскольку  =
=  =
= 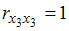 и
и  =
=  =
=  =0.
=0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
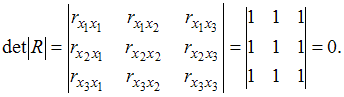
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Эконометрика: учеб. / И.И. Елисеева и [др.]; под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – С. 111–117.
Магнус, Ян Р. Эконометрика: нач. курс: [учеб. для студентов вузов по экон. специальностям] / Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий; Акад. нар. хоз-ва при Правительстве РФ. – М.: Дело, 2005. – С. 98–100.
|
|
|


