 |
Полный дифференциал функции двух переменных и его применение в приближенных вычислениях.
|
|
|
|
Пусть задана функция двух переменных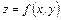 
. Легко доказать, что если приращение функции
(4)
можно представить в виде
, (5)
где 
и 
- некоторые константы, а 
, то в точке 
существуют частные производные этой функции, причем
, 
.
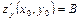Таким образом, при условии существования частных производных функции 
в точке выражение (5) можно записать в виде:
. (6)
При выполнении формулы (6) функция называется дифференцируемой в точке и выражение
,
то есть линейная часть приращения функции называется ее полным дифференциалом и обозначается символом 
или 
.
Под дифференциалами независимых переменных понимают произвольные приращения 
, 
, поэтому полный дифференциал функции можно записать в виде:
или
.
Слагаемые, стоящие в правой части последнего равенства называются частными дифференциалами функции . Таким образом, полный дифференциал функции равен сумме ее частных дифференциалов.
Полный дифференциал функции нескольких переменных (в нашем случае двух) с успехом применяется в приближенных вычислениях при оценке погрешностей. Пусть, например, мы имеем функцию 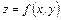двух переменных. При определении значений независимых переменных 
и 
будем допускать погрешности и соответственно. Тогда значение 
, вычисленное по неточным значениям аргументов, также получится с погрешностью
.
Оценим эту погрешность.
Заменим приближенно приращение функции ее дифференциалом (это оправдано лишь при достаточно малых значениях и ). Получим
.
Здесь и погрешности , , и коэффициенты при них могут быть как положительными, так и отрицательными; заменяя те и другие их абсолютными величинами, придем к неравенству:
.
Если через 
, 
, 
обозначить максимальные абсолютные погрешности (или границы для абсолютных погрешностей), то можно, очевидно, принять
|
|
|
. (7)
При этом само приближенное значение функции вычисляется по формуле:
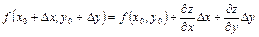. (8)
Пример 4. Дана функция 
и точка 
. С помощью дифференциала вычислить приближенные значения функции в данной точке.
Пусть 
, 
, тогда 
, 
.
По формуле (8) вычислим значение функции:
.
Вычислим отдельно частные производные заданной функции:
;
.
Вычислим значения функции и частных производных в точке 
:
;
;
.
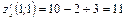Тогда
Ответ: 
________________________________________________________________________
Решение 0-варианта
(часть1)
1. Сделать разложение функции по формуле Тейлора при указанном значении 
:
.
Находим производные и подметив закономерность, запишем выражение для n-ой производной
.
Легко заметить,что n-я производная будет равна
.
Умножив числитель и знаменатель на (-1)(-2), 
запишется в виде:
Используя формулу (8) получим:
2.. Составить уравнение касательной и нормали к кривой 
в точке 
.
Решение: Найдем сначала 
,
подставляя координату 
точки , получаем
.
Подставляя 
в формулу (2), находим уравнение касательной
или 
.
Подставляя в формулу (3), выводим уравнение нормали
или 
.
Тангенс угла, образованного касательной с осью абсцисс, равен 
, откуда 
.
Ответ: уравнение касательной ; нормали ; угол
. 3. Дана функция 
. Показать, что 
.
Решение. Вычислим частные производные:
Тогда
что и требовалось доказать.
4. Дана функция 
и точка 
. С помощью дифференциала вычислить приближенное значение функции в данной точке ..
Решение.
Пусть 
, , тогда 
, 
.
По формуле (8) вычислим значение функции:
.
Вычислим отдельно частные производные заданной функции:
;
.
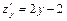Вычислим значения функции и частных производных в точке :
;
;
.
Тогда
__________________________________________
Основные теоретические сведения для
выполнения заданий 1-9
(часть 2)
Неопределенный интеграл.
Пусть дана функция 
. Функция 
называется первообразной для подынтегральной функции или интегралом от , если является производной для функции 
, т.е. 
и 
. Например, для функции 
первообразной будет функция 
, т.к. 
.
|
|
|
Если является первообразной для , то и 
, где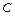 
- произвольная константа, также будет являться первообразной для , поскольку производная от константы равна нулю. Совокупность всех первообразных функций для функции называется неопределенным интегралом и обозначается 
. Таким образом:
. (1)
Из определения неопределенного интеграла вытекают формулы:
(2)
(3)
Формула (3) может быть использована для проверки правильности интегрирования.
Геометрически неопределенный интеграл можно интерпретировать как бесконечное множество кривых , сдвинутых относительно друг друга на произвольную константу вдоль оси .
2. Формулы интегрирования и таблица основных интегралов.
, а – константа.
1. 
.
2. 
, 
.
3. 
.
4. 
.
5. 
.
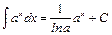6. 
.
7. 
.
8. 
.
9. 
.
10. 
.
11. 
.
Вычисление любого сложного интеграла, выражающегося через элементарные функции путем преобразований (если это необходимо), сводится к вычислению интегралов, представленных в таблице. Если интеграл табличный, то интегрирование осуществляется сразу.
Пример 1. Вычислить интеграл
.
Разбиваем интеграл на три интеграла и интегрируем:
Дифференцированием первообразной проверим правильность интегрирования:
Полученное выражение совпадает с подынтегральной функцией, т.е. интегрирование проведено правильно.
|
|
|
