 |
Д и ф ф е р е н ц и а л ь н ы е у р а в н е н и я
|
|
|
|
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, функцию и производные (или дифференциалы) этой функции.
Определение. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Дифференциальные уравнения первого порядка.
Уравнения с разделяющимися переменными
Самыми простыми дифференциальными уравнениями являются уравнения первого порядка:
.
Определение. Частным решением уравнения первого порядка называется решение, удовлетворяющее заданному начальному условию
,
где 
- заданная постоянная величина.
Самыми простыми дифференциальными уравнениями первого порядка являются уравнения вида
. (1)
Такие уравнения решаются простым интегрированием функции, т.е.
. (2)
Следующими по сложности являются дифференциальные уравнения вида
, (3)
для которых дифференциальная форма такова:
. (4)
Поскольку в уравнении (4) левая часть содержит лишь переменную 
и ее дифференциал, а правая – лишь переменную 
и ее дифференциал, то говорят, что в этом уравнении переменные и разделены.
Чтобы решить уравнение (4), нужно проинтегрировать обе его части:
. (5)
К решению уравнений вида (4) сводится интегрирование дифференциальных уравнений с разделяющимися переменными. Так называют уравнение
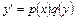, (6)
правая часть которого является произведением функции от на функцию от .
Пример 1. Решить уравнение
.
Решение. Это уравнение с разделяющимися переменными. Приведем его к виду (4), т.е. разделим переменные:
.
Получили уравнение с разделенными переменными. Проинтегрируем обе части полученного уравнения:
|
|
|
;
В силу произвольности константы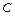 
положим 
и запишем полученное равенство в виде:
Из школьного курса алгебры известна формула:
.
Тогда
Окончательно будем иметь:
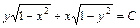- общее решение (или общий интеграл) данного дифференциального уравнения.
Ответ: .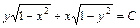
Линейные уравнения первого порядка
Определение. Линейным уравнением первого порядка называют дифференциальное уравнение первого порядка, которое линейно относительно функции и ее производной, т.е. уравнение вида
. (7)
Здесь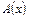 
, 
, 
- непрерывные функции от . В области, где 
, это уравнение равносильно уравнению вида
. (8)
Проще всего решается линейное дифференциальное уравнение в том случае, когда его правая часть равна нулю, т.е. уравнения вида:
. (9)
Такое уравнение называют однородным линейным уравнением первого порядка. Оно является уравнением с разделяющимися переменными.
Уравнение (8) в общем случае, т.е. когда 
, называют неоднородным линейным уравнением первого порядка. Такое уравнение решается с помощью замены
. (10)
При этом уравнение (8) принимает вид:
. (11)
Бернулли доказал, что уравнение (11) разрешимо только в случае, если
. (12)
При выполнении равенства (12) из равенства (11) также следует, что
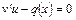. (13)
Таким образом, для решения уравнения (11) нужно сначала из уравнения (12) найти функцию 
, а затем, подставив найденную функцию в уравнение (13), найти функцию 
, после чего подставить в равенство (10) эти две функции.
Пример 2. Найти общее решение уравнения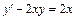 
.
Решение. Пусть 
, тогда 
. Данное уравнение примет вид:
.
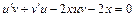Так как 
, то
Найдем 
из полученного равенства:
.
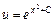В силу произвольности константы 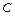положим 
.
Тогда
.
.
Подставим в это равенство найденную функцию .
.
Разделим переменные:
.
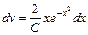Проинтегрируем обе части полученного равенства:
Подставим найденные функции и 
в равенство (10):
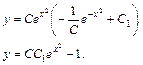
В силу произвольности констант 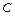и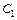 
положим 
.
Тогда искомое общее решение имеет вид:
|
|
|
.
Ответ: .
Подобным образом решается уравнение Бернулли:
. (14)
Однородные уравнения
Рассмотрим еще один класс уравнений, которые путем подстановки сводятся к уравнениям с разделяющимися переменными.
Определение. Функция 
называется однородной функцией нулевой степени, если для любого 
выполняется равенство
. (15)
Иными словами, однородная функция нулевой степени не изменяется при умножении и на одно и то же число.
Определение. Дифференциальные уравнения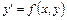 
, правая часть которых является однородной функцией нулевой степени называются однородными уравнениями.
Однородные уравнения решаются с помощью замены 
. Эта замена приводит однородные уравнения к уравнениям с разделяющимися переменными.
Пример 3. Решить уравнение 
.
Решение. Разрешим данное уравнение относительно 
:
.
Это уравнение однородно, т.к. его правая часть – однородная функция нулевой степени.
Сделаем подстановку
,
тогда
,
,
,
,
,
,
.
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения:
,
.
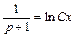Сделаем обратную замену 
.
,
,
,
- общий интеграл.
Ответ: .
.
|
|
|
