 |
Ряды с положительными членами
|
|
|
|
Рассмотрим достаточные признаки сходимости ряда.
1. Признак сравнения.
Пусть даны два ряда с положительными членами
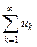 (30)
(30)
и
 , (31)
, (31)
и пусть каждый член ряда (30) не больше соответствующего члена ряда (31), т.е.  начиная с некоторого номера
начиная с некоторого номера  , тогда
, тогда
1) если сходится ряд (31), то сходится ряд (30);
2) если расходится ряд (30), то расходится и ряд (31).
2. Предельный признак сравнения.
Если  , то ряды (30) и (31) ведут себя одинаково, т.е. если расходится ряд (30), то расходится и ряд (31), и наоборот, если сходится ряд (30), то сходится и ряд (31).
, то ряды (30) и (31) ведут себя одинаково, т.е. если расходится ряд (30), то расходится и ряд (31), и наоборот, если сходится ряд (30), то сходится и ряд (31).
Обычно применяют признаки сравнения с известными сходящимися или расходящимися рядами. Так, известно, что обобщенный гармонический ряд  сходится, если
сходится, если  и расходится, если
и расходится, если  .
.
Пример 13. Выяснить, сходится ли ряд  .
.
Решение. Сравним данный ряд с известным сходящимся гармоническим рядом  :
:
 , следовательно, оба ряда ведут себя одинаково, т.е. сходятся.
, следовательно, оба ряда ведут себя одинаково, т.е. сходятся.
Ответ: данный ряд сходится.
3. Признак Даламбера.
Пусть дан ряд
 (32)
(32)
Если при  существует предел модуля отношения последующего члена к предыдущему
существует предел модуля отношения последующего члена к предыдущему  , равный
, равный  :
:
 ,
,
то при  ряд сходится, при
ряд сходится, при  ряд расходится.
ряд расходится.
При  ряд может быть как сходящимся, так и расходящимся, и необходимо применить другой признак сходимости ряда.
ряд может быть как сходящимся, так и расходящимся, и необходимо применить другой признак сходимости ряда.
Пример 14. Выяснить, сходится ли ряд  .
.
Решение. Здесь  ,
,  . Поэтому
. Поэтому  , следовательно, данный ряд сходится.
, следовательно, данный ряд сходится.
Ответ: данный ряд сходится.
4. Радикальный признак Коши.
Пусть дан ряд (32).
Если при  существует предел корня n-ой степени из модуля общего члена, равный
существует предел корня n-ой степени из модуля общего члена, равный  :
:
 ,
,
то при  ряд сходится, при
ряд сходится, при  ряд расходится.
ряд расходится.
При  ряд может быть как сходящимся, так и расходящимся.
ряд может быть как сходящимся, так и расходящимся.
Пример 15. Выяснить вопрос о сходимости ряда  .
.
Решение. Применим радикальный признак Коши. Здесь  .
. 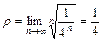 , следовательно, данный ряд сходится.
, следовательно, данный ряд сходится.
|
|
|
Ответ: данный ряд сходится.
5. Интегральный признак Коши.
Пусть дан ряд (32), члены которого являются значениями непрерывной функции  при целых значениях аргумента
при целых значениях аргумента  , и пусть
, и пусть  монотонно убывает в интервале
монотонно убывает в интервале 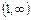 . Тогда ряд сходится, если сходится несобственный интеграл
. Тогда ряд сходится, если сходится несобственный интеграл  , и расходится, если этот интеграл расходится.
, и расходится, если этот интеграл расходится.
Пример 16. Рассмотрим ряд  . К этому ряду не применим ни признак Даламбера, ни радикальный признак Коши (при применении признака Даламбера или радикального признака Коши получим
. К этому ряду не применим ни признак Даламбера, ни радикальный признак Коши (при применении признака Даламбера или радикального признака Коши получим  ). Применим интегральный признак Коши:
). Применим интегральный признак Коши:

Таким образом, мы доказали, что гармонический ряд сходится при  и расходится при
и расходится при  .
.
Ряды с произвольными членами
В случае, если члены ряда попеременно имеют то положительный, то отрицательный знак, то ряд называют знакочередующимся. В этом случае справедлива теорема Лейбница: Если в знакочередующимся ряде абсолютные значения членов убывают и n-ый член стремится к нулю при  , то ряд сходится, причем его сумма по абсолютной величине меньше первого члена ряда.
, то ряд сходится, причем его сумма по абсолютной величине меньше первого члена ряда.
Для рядов с произвольным распределением знаков их членов справедлив достаточный признак сходимости: Если ряд, составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд.
В случае, если сходится ряд, составленный из абсолютных величин членов данного ряда, говорят об абсолютной сходимости ряда. Если данный ряд сходится, а ряд, составленный из абсолютных величин членов данного ряда расходится, то говорят, что данный ряд сходится условно или неабсолютно.
Степенные ряды.
Ряды, членами которых являются не числа, а функции независимой переменной  называют функциональными рядами.
называют функциональными рядами.
Определение. Степенным рядом называется функциональный ряд
 ,
,
члены которого суть произведение постоянных  на степенные функции с целыми показателями степеней от разности
на степенные функции с целыми показателями степеней от разности  .
.
Постоянные  называют коэффициентами степенного ряда.
называют коэффициентами степенного ряда.
|
|
|
В частности, если 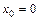 , то мы будем иметь степенной ряд:
, то мы будем иметь степенной ряд:
 (33)
(33)
Теорема Абеля. Если степенной ряд (33) сходится при 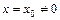 , то он сходится, и притом абсолютно, при всяком
, то он сходится, и притом абсолютно, при всяком  , лежащем в интервале
, лежащем в интервале  , т.е. удовлетворяющем условию
, т.е. удовлетворяющем условию  .
.
Определение. Радиусом сходимости степенного ряда (33) называется такое число  , что для всех
, что для всех  ,
,  , степенной ряд сходится, а для всех
, степенной ряд сходится, а для всех  ,
,  , расходится. Интервал от
, расходится. Интервал от  до
до  называется интервалом сходимости степенного ряда.
называется интервалом сходимости степенного ряда.
Степенной ряд в интервале его сходимости можно интегрировать и дифференцировать почленно.
Ряд Тейлора
Определение. Рядом Тейлора функции  в окрестности точки
в окрестности точки  называется степенной ряд
называется степенной ряд
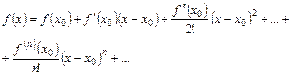 (34)
(34)
относительно разности  , коэффициенты которого
, коэффициенты которого  ,
,  ,…,
,…,  ,… выражаются через функцию
,… выражаются через функцию  и ее производные в точке
и ее производные в точке  по формулам
по формулам
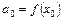 ,
, 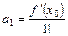 ,
,  ,…,
,…,  ,…
,…
Эти коэффициенты называются коэффициентами Тейлора функции  в точке
в точке  .
.
Обозначим через  многочлен
многочлен  -ой степени, равный сумме первых
-ой степени, равный сумме первых  членов ряда Тейлора:
членов ряда Тейлора:

Разность
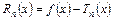
называется остаточным членом ряда Тейлора.
Для того, чтобы ряд Тейлора при значении  сходился и имел своей суммой
сходился и имел своей суммой  , т.е.
, т.е.
 ,
,
необходимо и достаточно, чтобы
 ,
,
т.е. остаточный член ряда Тейлора должен стремиться к нулю при  .
.
Заметим, что особенно часто используется разложение функций по степеням  . В этом случае, полагая в (34)
. В этом случае, полагая в (34) 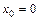 , получаем ряд
, получаем ряд
 , (35)
, (35)
который называется рядом Маклорена.
|
|
|


