 |
Системы дифференциальных уравнений
|
|
|
|
Определение. Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входит независимая переменная, искомые функции и их производные.
Определение. Нормальной системой дифференциальных уравнений называется система дифференциальных уравнений вида:
 (23)
(23)
Решением такой системы называется совокупность  функций
функций  ,
,  ,…,
,…,  , удовлетворяющих всем уравнениям системы.
, удовлетворяющих всем уравнениям системы.
Частным решением системы (23) называется решение, удовлетворяющее заданным начальным условиям
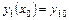 ,
,  ,…,
,…,  ,
,
где  ,
, 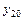 ,…,
,…,  - заданные постоянные величины.
- заданные постоянные величины.
Как правило, любую систему дифференциальных уравнений можно привести к нормальной, ей эквивалентной.
Любое дифференциальное уравнение  -го порядка, разрешенное относительно старшей производной, с помощью введения новых вспомогательных функций всегда можно свести к нормальной системе дифференциальных уравнений.
-го порядка, разрешенное относительно старшей производной, с помощью введения новых вспомогательных функций всегда можно свести к нормальной системе дифференциальных уравнений.
В обычно встречающихся случаях верно и обратное утверждение:
Нормальная система уравнений может быть заменена одним дифференциальным уравнением, порядок которого равен числу уравнений системы.
В приложениях обычно часто встречаются системы линейных уравнений с постоянными коэффициентами:
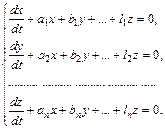
где 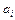 ,
,  ,…,
,…,  - постоянные величины.
- постоянные величины.
Рассмотрим систему двух линейных уравнений с постоянными коэффициентами:
 (24)
(24)
Приведем без доказательства следующие свойства системы (24):
1) Если известна частная система решений  ,
,  системы уравнений (24), то функции
системы уравнений (24), то функции 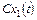 ,
, 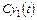 , где
, где 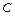 - произвольная константа, также образуют систему решений.
- произвольная константа, также образуют систему решений.
2) Если известны две системы решений  ,
,  и
и  ,
,  , то и функции
, то и функции  ,
,  также являются решениями и при этом функции
также являются решениями и при этом функции  представляют систему решений при любых постоянных
представляют систему решений при любых постоянных 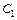 и
и  .
.
Если заданы начальные условия 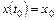 ,
,  , то система уравнений для определения постоянных
, то система уравнений для определения постоянных 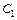 и
и  примет вид:
примет вид:
|
|
|

где 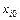 ,
, 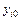 - значения соответствующих функций при
- значения соответствующих функций при  . Для того, чтобы эта система имела единственное решение при любых начальных условиях, необходимо и достаточно, чтобы определитель
. Для того, чтобы эта система имела единственное решение при любых начальных условиях, необходимо и достаточно, чтобы определитель

ни при каком значении  не обращался в нуль. Будем говорить, что совокупность двух систем, удовлетворяющих этому условию, образует фундаментальную систему.
не обращался в нуль. Будем говорить, что совокупность двух систем, удовлетворяющих этому условию, образует фундаментальную систему.
Структура решения системы (24):
 ,
, 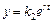 , (25)
, (25)
где  ,
,  и
и  - неопределенные постоянные коэффициенты, которые следует определить.
- неопределенные постоянные коэффициенты, которые следует определить.
Дифференцируя функции  и
и  и подставляя в систему (24), получим:
и подставляя в систему (24), получим:

Сократив на 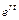 , приходим к системе линейных однородных уравнений относительно
, приходим к системе линейных однородных уравнений относительно  и
и  :
:
 (26)
(26)
Чтобы эта система имела ненулевые решения, необходимо и достаточно, чтобы ее определитель был равен нулю:
 .
.
Раскрыв этот определитель, получим уравнение второй степени относительно  . Это уравнение называется характеристическим.
. Это уравнение называется характеристическим.
Итак, для того, чтобы существовало решение вида (25), необходимо и достаточно, чтобы число  было корнем характеристического уравнения.
было корнем характеристического уравнения.
В дальнейшем будем полагать, что характеристическое уравнение имеет только простые корни.
Допустим, что один из действительных корней равен 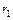 . Подставим это значение в систему уравнений (26), получим:
. Подставим это значение в систему уравнений (26), получим:
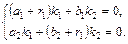
Можно доказать, что полученные уравнения линейно зависимы, т.е. одно из уравнений получается из другого умножением обеих частей на постоянный множитель. Решение такой системы будет зависеть от одной произвольной постоянной. Поступая так со всеми корнями характеристического уравнения, мы найдем две системы функций, каждая из которых является решением системы (24):

Эти функции образуют фундаментальную систему.
Тогда общее решение системы (24) запишется в виде:

В случае комплексно сопряженных корней характеристического уравнения 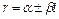 действительные решения имеют вид
действительные решения имеют вид  и
и  . В этом случае удобнее сразу записать, что
. В этом случае удобнее сразу записать, что  ,
,  (т.е. положить
(т.е. положить  ) и находить функции
) и находить функции  ,
,  , выражая их через функции
, выражая их через функции  и
и  и их производные.
и их производные.
|
|
|
Пример 8. Решить систему

Решение. Запишем данную систему в виде:

Характеристическое уравнение системы имеет вид:
 .
.
Откуда
 .
.
Следовательно,  ,
, 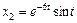 . Из первого уравнения имеем:
. Из первого уравнения имеем:
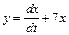 .
.
Подставляя вместо  найденное выражение, получим:
найденное выражение, получим:
 ,
,  .
.
Эти решения образуют фундаментальную систему и, следовательно, общим решением системы будет

|
|
|


