 |
Вычислить несобственные интегралы или доказать их расходимость.
|
|
|
|
,
т.е. интеграл расходится.
3.Вычислить объем тела, полученного вращением кривых 
и 
вокруг оси 
.
Делаем рисунок (Рис. 7).
Находим точку пересечения кривых: 
; 
; 
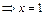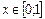. Используем формулу (24). Объем искомого тела получится вычитанием из объема тела, полученного вращением кривой , объема тела, полученного вращением кривой :
ед. куб.» 
ед. куб.
4. В области 
, ограниченной заданными линиями, вычислить двойной интеграл двумя способами (т.е. изменяя порядок интегрирования по 
и 
). Сделать рисунок.
; 
; 
.
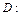
Область образована пересечением 2–х окружностей (Рис. 9).
Для определенности в качестве области выберем заштрихованную область. Из равенства абсцисс и ординат окружностей в точках пересечения находим координаты точек 
и 
:
, т.е. 
, 
.
Перейдем к двукратному интегралу.
а) во внешнем интеграле интегрируем по 
2 – й интеграл подстановкой 
сводится к табличному интегралу. В 1 – м интеграле делаем подстановку
. Таким образом:
Суммируя все слагаемые, получим 
;
б) во внешнем интеграле интегрируем по . В этом случае во внутреннем интеграле, при интегрировании по , необходимо отдельно рассмотреть области 
и 
. Т.о., получим:
.
В первом интеграле делаем замену переменной:
,
,
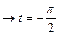Во втором интеграле делаем замену переменной:
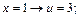
Получим:
Результаты вычислений совпали.
5. С помощью тройного интеграла вычислить объем тела, ограниченного заданными поверхностями. Сделать рисунки областей 
и .
V: 
Решение.
Изображаем области и (Рис. 10, 11). В качестве выступает объем 4-гранной пирамиды. Областью на плоскости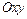 
является равносторонний треугольник. Если в 3 – х кратном интеграле в качестве внешнего интеграла выбрать интеграл по 
, то в интеграле по , как это видно из рис. 11, 
. Пределы интегрирования интеграла по 
изменяются на отрезке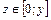 
. Т.о., запишем тройной интеграл в виде 3 – х кратного:
|
|
|
6. Найти общее решение дифференциального уравнения.
а) 
; б) 
;
в) 
; г) 
.
Решение.
а) .
Выразим 
:
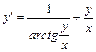- однородное уравнение.
Воспользуемся заменой 
, тогда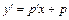 
, 
.
.
Упростим:
.
Разделим переменные:
.
Проинтегрируем обе части полученного равенства:
,
,
.
Тогда
;
.
Произведем обратную замену 
, окончательно получим:
- общее решение.
Ответ: .
б) .
Выразим :
- линейное неоднородное уравнение 1-го порядка.
Воспользуемся заменой 
, тогда 
.
.
,
.
Разделим переменные:
.
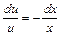Проинтегрируем обе части полученного равенства:
,
.
Упростим:
.
Тогда
,
,
,
.
Произведем обратную замену
,
- общее решение.
Ответ: .
в) 
.
Выразим :
- уравнение Бернулли.
Произведем замену , тогда .
.
,
,
,
.
Проинтегрируем обе части полученного равенства:
,
.
.
Тогда
,
.
Разделим переменные:
.
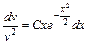Проинтегрируем обе части полученного равенства:
.
,
.
Произведем обратную замену:
,
- общий интеграл.
Ответ: .
г) 
.
Положим 
, тогда 
.
Разделим переменные:
.
Проинтегрируем обе части полученного равенства:
.
,
.
Произведем обратную замену:
.
Проинтегрировав полученное равенство, будем иметь:
- общее решение.
Ответ: .
7. Для данного дифференциального уравнения второго порядка найти частное решение, удовлетворяющее заданным начальным условиям: 
, 
, 
.
Решение. Характеристическое уравнение имеет вид:
.
Корни этого уравнения 
.
Тогда общее решение соответствующего однородного уравнения:
.
Будем искать частное решение в виде:
Вычислим производные функции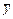 
до второго порядка:
Подставим полученную производную и функцию 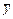в исходное уравнение:
Сгруппируем в левой части равенства слагаемые, содержащие 
и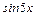 
:
Тогда
,
.
Отсюда
Из этой системы уравнений находим:
|
|
|
.
Частное решение имеет вид:
.
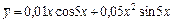Тогда общее решение неоднородного уравнения:
.
Используем начальные условия:
.
.
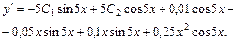
Решение задачи Коши имеет вид:
Ответ: .
8. Исследовать на сходимость ряды:
а)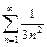 
; б) 
;
в) 
; г) 
Решение.
а) .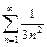
Сравним данный ряд со сходящимся рядом 
.
,
следовательно ряды ведут себя одинаково. Данный ряд сходится.
Ответ: данный ряд сходится.
б) .
Воспользуемся признаком Даламбера.
следовательно, согласно признаку Даламбера, данный ряд сходится.
Ответ: данный ряд сходится.
в) .
Сначала докажем, что сходится ряд 
Для этого воспользуемся интегральным признаком.
.
Интеграл сходится, следовательно, сходится и ряд
Воспользуемся предельной теоремой сравнения рядов 
и
.
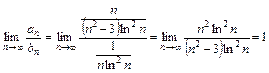Ряды являются эквивалентными, значит, из сходимости ряда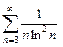 
следует сходимость ряда .
Ответ: данный ряд сходится.
г)
Применим к данному знакочередующемуся ряду радикальный признак Коши.
.
Следовательно, данный ряд сходится.
Ответ: ряд сходится.
9. Разложить в ряд Фурье функцию 
на отрезке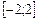 
.
Решение.
По формулам (38) найдем:
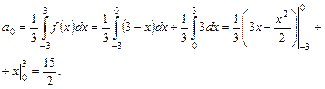
Подставим найденные значения коэффициентов ряда Фурье в формулу (38):
.
Ответ: .
Литература.
1. Баврин И.И., Матросов В.Л. Высшая математика – М. ВЛАДОС, 2002
2. Бахвалов С.В., Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии. М.: Наука, 1964 (или любое другое издание).
3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -М.. Наука, 1971 (или любое другое издание).
4. Берман Г.Н. Сборник задач по курсу математического анализа. - М.: Изд. технике теоретической литературы 1951-1956. (или любое другое издание).
5. Высшая математика для экономистов. Под ред. Н. Ш. Кремера. – М. ЮНИТИ. 2001.
6. Кудрявцев Л.Д. Математический анализ. В 2-х тт. - М.: Высшая школа,1973 (или любое другое издание).
7. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. -М.: Наука, 1975-1990.
8. Математика в понятиях и терминах. Под ред. Л.В.Сабинина. В 2-х тт. -М.: Просвещение, 1978, 1982.
9. Матросов В.Л., Основы курса высшей математики – М., ГИЦВ, 2002.
10. Никольский С.М. Курс математического анализа. - М.: Наука, В 2-х тт.1973 (или любое другое издание).
11. Пискунов Н.С. Дифференциальное и интегральное исчисления. В 2-х тт.-М.:Наука, 1970-1985.
|
|
|
12. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. В 2-х ч.М. «Финансы и статиститка».2001.
13. Степанов В.В. Курс дифференциальных уравнений (любое издание).
14. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. - М.: Наука, 1972 (или любое другое издание).
15. Федорюк М.В. Обыкновенные дифференциальные уравнения. - М.:Наука, 1980,1985.
16. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. - М.:Наука, 1992.
17..Фихтенгольц Г.М. Основы математического анализа. В 2-х тт. - М.:Наука, 1968 (или любое другое издание).
18. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. В 3-х тт. – М.: Наука., 1970 (или любое другое издание).
19. Цубербиллер Щ.Н. Задачи и упражнения по аналитической геометрии. – М.: Наука, 1964. (или любое другое издание)
20. Шипачев В. П. Высшая математикаю – М.: Высшая школа, 1982-1990.
|
|
|
