 |
Интегрирование рациональных дробей.
|
|
|
|
Пусть дан интеграл вида
,
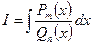где 
и 
- полиномы (многочлены) степен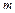и 
и 
соответственно. Подынтегральная функция в этом случае будет называться правильной рациональной дробью, если 
и неправильной рациональной дробью, если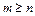 
. Интеграл 
в общем случае можно вычислить, если только . Если 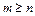, то необходимо провести деление полинома на полином . В результате получается выражение вида:
, (5)
где полином 
называется целой частью исходного выражения, а 
- остатком от деления. Второе слагаемое в (5) при этом является правильной дробью, т.е. 
.
Пример 6. Представить неправильную дробь
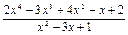
в виде целой части и правильной дроби.
Делаем деление:
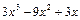
Таким образом:
.
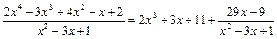Интегрирование целой части в (5) не представляет труда. Для интегрирования правильной дроби, если 
, необходимо разложение второго слагаемого в (5) на более простые дроби. Считая, что коэффициент при 
в равен единице (если он не равен единице, то этого можно добиться очевидным образом), полином с вещественными коэффициентами можно, как доказывается в алгебре, единственным образом записать в виде:
(6)
где 
- натуральные числа, 
- вещественные числа, а множители вида 
не имеют вещественных корней (т.е. дискриминант отрицателен). Тогда второе слагаемое в (5) можно представить в виде:
(7)
где 
- константы.
Как видно из (7), каждому множителю в правой части (6) соответствует столько дробей в правой части (7), какова кратность этого множителя.
Константы 
, 
, 
находятся из системы уравнений, которая получается следующим образом. Все дроби в правой части равенства (7) приводятся к общему знаменателю. В числителе правой части собираются слагаемые с одинаковыми степенями 
и коэффициенты при них приравниваются к коэффициентам при 
в соответствующих степенях в полиноме 
. В результате получается система уравнений для определения искомых констант.
|
|
|
Пример 7. Вычислить интеграл
Т.к. степень полинома в числителе больше степени полинома в знаменателе, то разделим числитель на знаменатель, предварительно перемножив сомножители в знаменателе:
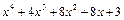
В результате интеграл перепишется в виде:
.
Первый интеграл легко вычисляется: он равен 
. Прежде чем вычислять второй интеграл (обозначим его 
), необходимо выяснить, вещественны или комплексны корни уравнения
. (8)
От вида корней зависит вид разложения подынтегральной функции в по формуле (7). Т.к. корни уравнения (8) комплексные (дискриминант 
), то разложение подынтегральной функции в по формуле (7) имеет вид:
После приведения правой части равенства к общему знаменателю получим:
или
Приравнивая коэффициенты при одинаковых степенях в левой и правой части равенства, получим систему уравнений:
Решая эту систему, найдем:
, 
, 
, 
.
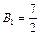Таким образом,
.
В последнем интеграле знаменатель приводим к полному квадрату:
.
В результате интеграл дает арктангенс. Окончательно получим:
Интегрирование иррациональных выражений.
Интегралы вида
,
где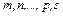 
- целые числа, сводятся к интегралу от рациональных функций заменой переменной 
, где 
- наименьшее общее кратное чисел 
(НОК 
). Аналогичная подстановка делается, если вместо содержатся выражения вида 
или 
.
Пример 8. Вычислить интеграл
.
Т.к. НОК (2;3)=6, то делаем подстановку:
и
=
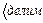
Переходя к переменной , получим:
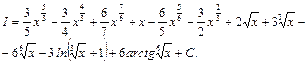
Интегралы вида 
, где 
- вещественные числа, в общем случае вычисляются одной из подстановок Эйлера:
, 
; (9)
, 
; (10)
или 
, (11)
где 
и 
- различные вещественные корни трехчлена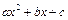 
.
Пример 9. Вычислить интеграл
.
Используем 1–ю подстановку Эйлера (9): 
. Возведем в квадрат обе части равенства. После сокращения 
получим:
|
|
|
;
выразим теперь радикал через переменную 
:
.
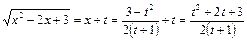Подставляя выраженные через 
величины в , получим:
.
Делая подстановку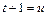 
; 
, получим:
|
|
|
