 |
Интегрирование тригонометрических функций.
|
|
|
|
Интегралы вида 
в общем случае вычисляются подстановкой 
. При этом
, 
, 
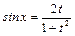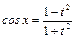(12)
и подынтегральная функция станет рациональной функцией от 
.
Пример 10. Вычислить интеграл
.
Делая подстановку и используя формулы (12), интеграл запишем в виде:
Интегралы вида 
, где 
- целые числа, удобно вычислять подстановкой 
.
Интегралы вида 
, где 
- числа разной четности, вычисляются подстановкой 
, если 
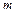четно и 
, если 
четно.
Интегралы вида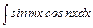 
; 
; 
, где 
, вычисляются с использованием формул тригонометрии, преобразующих произведение тригонометрических функций в их сумму.
Определенный интеграл.
Пусть дана непрерывная на отрезке 
функция 
. Разобьем точками 
, 
на 
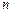отрезков длиной 
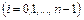(рис. 1) и составим сумму
, (13)
которая называется интегральной суммой для функции на отрезке .
Каждое слагаемое этой суммы приближенно равно площади прямоугольника высотой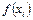 
и с основанием 
, поэтому вся сумма (13) будет приближенно равна площади криволинейной трапеции, ограниченной прямыми 
, 
, отрезком на оси 
и кривой .
Если функция непрерывна на отрезке , то при всех 
существует предел суммы (13), не зависящий от способа разбиения отрезка . Этот предел называется определенным интегралом от функции на отрезке и обозначается 
. Т.о.:
(14)
и формула (14) дает точное значение площади криволинейной трапеции.
Определенный интеграл вычисляется по формуле Ньютона – Лейбница:
, (15)
где 
- первообразная для функции 
.
Пример 11. Вычислить определенный интеграл
.
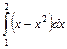Используя формулу (15), получим:
.
При интегрировании по частям определенного интеграла справедлива формула:
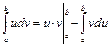. (15а)
Несобственные интегралы.
Интегралы с бесконечными пределами
Пусть функция определена в интервале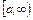 
. Тогда предел 
называется несобственным интегралом. Если этот интеграл существует (т.е. равен какому – то числу), то он называется сходящимся. Если предел равен бесконечности или не существует, то несобственный интеграл называется расходящимся. Аналогично определяются несобственные интегралы на интервалах 
и 
:
|
|
|
,
.
Пример 12. Вычислить несобственный интеграл
.
Приложения определенного интеграла.
1. Площадь области, ограниченной кривой 
, осью и прямыми 
и 
равна
(17)
(площадь участков с 
должна браться по модулю). При параметрическом задании функции 
, 
будет равна
. (18)
В полярной системе координат площадь 
, ограниченная кривой 
и двумя лучами 
и 
равна
. (19)
2. Длина дуги плоской, дифференцируемой на отрезке кривой, заданной уравнением , 
равна
. (20)
При параметрическом задании кривой 
, 
равна
. (21)
В полярной системе координат длина дуги кривой, заданной уравнением , где 
, находится по формуле
. (22)
3. Площадь поверхности, образованной вращением кривой 
вокруг оси , равна
. (23)
4. Объем тела, полученного вращением кривой вокруг оси 
, равен
. (24)
Двойной интеграл.
Интеграл вида
(32)
называется двойным интегралом от функции 
по заданной на плоскости 
замкнутой области 
. При этом функция предполагается непрерывной в области 
. Если 
, то интеграл 
(33)
в этом случае имеет смысл площади области . Если 
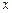и является определенной функцией 
и 
, то интеграл (32) имеет смысл объема тела, ограниченного сверху поверхностью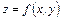 
, снизу плоскостью 
, а с боков поверхностью цилиндра, образующие которой параллельны оси 
, а направляющей является граница области .
Двойной интеграл обладает следующими свойствами:
1. 
, 
. (34)
2. 
. (35)
3. 
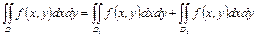, (36)
где 
.
Введем для границы области (Рис. 2) следующие обозначения:
дугу 
обозначим как кривую 
дугу 
обозначим как кривую 
дугу 
обозначим как кривую 
дугу 
обозначим как кривую 
.
|
|
|
Вычисление двойного интеграла осуществляется сведением его к двукратному (повторному) интегралу. Используя введенные обозначения можно записать
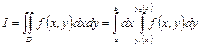. (37)
Левый интеграл (по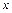 
) в (37) называется внешним интегралом, а правый интеграл (по ) – внутренним. Изменяя порядок интегрирования в двукратном интеграле, можно записать:
. (38)
Для правильной расстановки пределов интегрирования во внутреннем интеграле целесообразно внутри области провести прямую, параллельную оси переменной, по которой осуществляется интегрирование во внутреннем интеграле. Пересечение этой прямой с границами области указывает на значения пределов интегрирования.
Пример 16. Вычислить двойной интеграл 
, меняя порядок интегрирования по 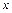и . Область ограничена кривыми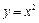 
и 
(Рис. 3).
Решение.
Делаем рисунок области . Находим координаты 
точки 
из равенства ординат обеих кривых в точке :
; 
; 
.
Записываем двойной интеграл в виде двукратного, рассмотрев 2 случая:
а) внутренний интеграл вычисляется по .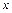
Проводим внутри области прямую 
(Рис. 3). Как видно, абсцисса на прямой изменяется от 
на верхней кривой до 
на нижней кривой. Значения y во внешнем интеграле изменяются от 
до 16. Т.о. имеем:
;
б) внутренний интеграл вычисляется по .
Проводим внутри области прямую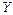 
(рис. 3). Ордината на прямой 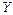изменяется от 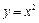на нижней кривой до 
на верхней кривой. Значения 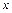во внешнем интеграле изменяются от до 
. Т. о. имеем:
.
Результаты вычисления интеграла двумя способами совпадают.
При вычислении двойного интеграла в полярных координатах в подынтегральном выражении делается замена: 
, 
, 
:
, (39)
где 
обозначены на рис. 4.
Тройной интеграл.
Пусть в пространстве в области 
, ограниченной замкнутой поверхностью 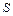, задана непрерывная функция 
. Тогда интеграл
(40)
называется тройным интегралом от функции по области .
Если – плотность вещества, то интеграл имеет смысл массы вещества, находящейся в объеме . Если 
, то
(41)
и интеграл (41) равен объему .
Вычисление тройного интеграла, аналогично двойному, делается сведением его к 3-х кратному интегралу. При этом область считается правильной, т.е. для нее выполняются следующие условия:
всякая прямая, параллельная оси , проведенная в , пересекает поверхность 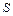лишь в двух точках;
|
|
|
область проецируется на плоскость 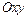в правильную область (т.е. любые прямые, параллельные осям и 
, проведенные в , пересекают границу области лишь в двух точках).
Сказанное в п. 2 справедливо для проекции и на другие координатные плоскости (
и 
).
Пусть поверхности 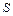, ограничивающие область снизу и сверху, описываются уравнениями: 
и 
соответственно.
На границе области обозначим через 
и 
уравнения дуг и , а через 
и 
– уравнения дуг и соответственно (рис. 5). Тогда интеграл (40) можно записать в виде 3 – х кратного интеграла
(42)
или
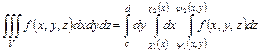. (43)
Пример 17. Вычислить интеграл 
, где область ограничена плоскостями 
, , 
, 
(рис. 6).
Область представляет собой пирамиду, верхняя поверхность которой описывается уравнением 
, а нижняя – уравнением 
. Проекцией области на плоскость 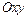является треугольник, уравнение гипотенузы которого есть 
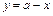(это уравнение получается из уравнения 
при ). При интегрировании по координата 
изменяется от до 
. При интегрировании по координата изменяется от до 
. Т.о., интеграл можно записать в виде 3–х кратного интеграла
|
|
|
