 |
Линейные дифференциальные уравнения высшего порядка с постоянными коэффициентами
|
|
|
|
Определение. Линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида
, (27)
где 
, 
- некоторые постоянные.
Определение. Уравнение
(28)
называется характеристическим уравнением для дифференциального уравнения (27).
Общее решение однородного линейного дифференциального уравнения
С постоянными коэффициентами
Определение. Однородным линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами называется уравнение вида
, (29)
где , - некоторые постоянные.
Если характеристическое уравнение для уравнения (29) имеет корни 
, , тогда
1) каждому 
-кратному действительному корню 
характеристического уравнения (29) соответствует частных решений вида 
, 
,…, 
;
2) каждой паре 
-кратных комплексно сопряженных корней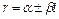 
характеристического уравнения (29) соответствует 
частных решений вида
, 
,…, 
,
, 
,…, 
.
Общая сумма кратностей всех корней должна равняться степени характеристического уравнения 
, поэтому число всех частных решений будет в точности совпадать с порядком уравнения.
Чтобы найти общее решение заданного уравнения, нужно взять линейную комбинацию указанных частных решений.
Пример 9. Решить уравнение 
.
Решение. Характеристическое уравнение имеет вид:
.
Корни этого уравнения 
, 
.
Тогда общее решение данного уравнения:
.
Ответ: .
Пример 10. Решить уравнение
.
Решение. Характеристическое уравнение
.
Методом подбора найдем, что один из корней 
, разделим многочлен на 
, получим:
или 
.
Корни этого уравнения 
, 
.
Поэтому общее решение заданного дифференциального уравнения запишется в виде:
.
Ответ: .
Общее решение неоднородного линейного дифференциального уравнения
|
|
|
С постоянными коэффициентами
Уравнение вида (27), в котором правая часть не является тождественным нулем называют неоднородным дифференциальным уравнением с постоянными коэффициентами.
Справедлива теорема о структуре общего решения неоднородного уравнения (27): Общее решение уравнения с правой частью (27) можно составить как сумму общего решения соответствующего однородного уравнения и какого-либо частного решения данного уравнения.
Оказывается, что частное решение уравнения (27), где правая часть
,
имеет вид
,
где 
, 
- многочлены степени, равной высшей из степеней многочленов 
, 
, а - кратность, с которой 
входят в число корней характеристического уравнения. Если не являются корнями характеристического уравнения, то принимаем равным нулю.
Пример 11. Решить уравнение 
.
Решение. Общее решение соответствующего однородного уравнения было найдено в примере 9 и имеет вид:
.
Так как величина 
(коэффициент при 
в степени второй экспоненты в правой части дифференциального уравнения) совпадает с однократным корнем 
характеристического уравнения, то будем искать частное решение в виде:
.
Вычислим производные функции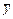 
до второго порядка:
.
Подставим полученные производные в исходное уравнение:
Упростим
Тогда 
, 
, 
. Отсюда
, 
, 
.
И частное решение имеет вид:
.
Тогда общее решение неоднородного уравнения:
.
Ответ: .
Р я д ы
Числовые ряды.
Пусть дана бесконечная последовательность чисел 
, 
,…, 
,…
Определение. Выражение 
называется числовым рядом, а , ,…, ,… - членами ряда.
Коротко ряд записывается так: 
.
Выражение для n -го члена ряда при произвольном n называется общим членом ряда.
Назовем n -ой частичной суммой ряда сумму его n первых членов:
.
Определение. Если при 
существует конечный предел последовательности частичных сумм членов данного ряда
|
|
|
,
то ряд называется сходящимся, а число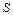 
- его суммой.
В противном случае ряд называют расходящимся.
Справедлив необходимый признак сходимости ряда: Если ряд сходится, то общий член стремится к нулю при неограниченном возрастании его номера.
Заметим, что этот признак является необходимым, но не достаточным, т.е. обратное утверждение не верно.
Пример 12. Рассмотрим ряд 
, который называется гармоническим.
Здесь 
при , но при этом ряд расходится 
.
Из необходимого признака сходимости ряда можно вывести достаточный признак расходимости ряда: Если общий член данного ряда при возрастании номера не стремится к нулю, то этот ряд является расходящимся.
|
|
|
