 |
Министерство образования и науки днр
|
|
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДНР
ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ
“ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ”
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению курсовой работы по курсу:
«Компьютерное моделирование физических процессов»
для студентов всех форм обучения
Донецк – 2017 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ
“ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ”
Кафедра “Электроснабжение промышленных
предприятий и городов”
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению курсовой работы по курсу:
«Компьютерное моделирование физических процессов»
для студентов всех форм обучения
утвержден
на заседании кафедры
" Электроснабжение
промышленных
предприятий и городов "
Протокол № ___________
от ____________________
утвержден
на заседании учебно-
издательского
совета ДонНТУ
Протокол №____
от ____________________
Донецк – 2017
УДК 681. 332 (07)
Методические указания к лабораторным работам по курсу " Компьютерное моделирование физических процессов" (для студентов специальности 7. 090603 " Электротехнические системы электропотребления" ) / Состав.: Джура С. Г., Шлепнёв С. В., Якимишина В. В., Фёдоров А. Ю.
Изложены теоретические сведения по методам вычислительной математики, используемых при решении инженерных задач в области электротехники и энергетики. Приведены задачи и методические рекомендации к выполнению 16 лабораторных работ, предназначенных для обучения студентов методам решения на ЭВМ линейных и нелинейных уравнений и их систем, дифференциальных уравнений, методам численного интегрирования, аппроксимации функций, поиска экстремальных значений.
|
|
|
Составители: С. Г. Джура, доц.
С. В. Шлепнёв, доц.
В. В. Якимишина, доц.
А. Ю. Фёдоров, асс.
Рецензент: В. М. Павлыш, проф.
Нормоконтролер: В. И. Чурсинов, доц.
ВВЕДЕНИЕ
Одним из главных направлений научно-технического прогресса в настоящее время является развитие методов и средств информатики и вычислительной техники.
Использование математических методов решения инженерных задач на ЭВМ позволяет значительно повысить эффективность процессов проектирования, расчета параметров, исследования, анализа и синтеза различных технических систем, в том числе и систем электроснабжения.
В математическом плане много задач электротехники и энергетики сводятся к решению алгебраических, трансцендентных и дифференциальных уравнений и их систем, операциям наматрицами, векторами и рядами, аппроксимации табличных функций, минимизации функционалов и др. Эти задачи не всегда могут быть решены аналитически и требуют применения численных методов.
В данном пособии приведены задачи и методические указания к лабораторным работам, выполнение которых позволит приобрести навыки алгоритмизации, программирования и решения на ЭВМ задач с использованием методов вычислительной математики.
По согласованию с преподавателем допускается замена задач, предусмотренных в лабораторных работах, задачами аналогичного содержания по дисциплинам, параллельно изучаются, или по тематике НИРС, а также выбор языка программирования, на котором будет выполняться задача.
Лабораторная работа 1
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ СТЕПЕННЫХ ПОЛИНОМОВ
ПО СХЕМЕ ГОРНЕРА
|
|
|
Цель работы: научиться вычислять значения степенных многочленов наиболее экономичным образом, приобрести навыки программирования с использованием функций и подпрограмм пользователя.
1. 1 Теоретические сведения
В практике анализа и синтеза систем автоматического управления и в теории электрических цепей часто возникает необходимость в исчислении функций, имеющих вид степенного полинома (многочлена):
| (1. 1) |
где n - степень полинома;
= ( 
) - вектор коэффициентов;
х - независимая переменная.
Многочлен (1. 1) можно преобразовать к виду:
 ,
| (1. 2) |
Алгоритм вычисления 
, составленный на основании выражения (1. 2), называется схемой Горнера.
Согласно этой (схеме многочлен i-го порядка выражают через многочлен (i-1) -го порядка по формуле:
 ,
| (1. 3) |
В математике доказано, что для многочленов общего вида нельзя построить алгоритм более экономичен в смысле числа операций (n добавлений и n умножений), чем схема Горнера.
1. 2 Задание
Рассчитать значение переменной z при x изменяющейся от -1 до +1 с шагом 0, 1. Выражения для вычисления z приведены в таблице 1. 1. В этих выражениях функции 
и 
представляют собой степенные многочлены, отличающиеся друг от друга порядком и значениями коэффициентов.
Для нечетных вариантов:
,
,
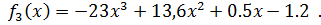
Для четных вариантов:
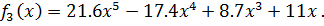
Для ввода значений коэффициентов степенных многочленов составить подпрограмму (процедуру), а для вычисления этих многочленов - функцию пользователя.
Таблица 1. 1 - Исходные данные к лабораторной работе №1
| № п/п | Выражение для вычисления переменной |
| 1, 2 | 
|
| 3, 4 | 
|
| 5, 6 | 
|
| 7, 8 | 
|
| 9, 10 | 
|
| 11, 12 | 
|
| 13, 14 | 
|
| 15, 16 | 
|
|
| |
| Продолжение таблицы 1. 1 | |
| 17, 18 | 
|
| 19, 20 | 
|
| 21, 22 | 
|
| 23, 24 | 
|
| 25, 26 | 
|
1. 3 Методические рекомендации
Пусть дан массив A(n), где n – номер порядкового элемента (рис 1. 1). Положив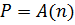 
и выполняем операцию по формуле 1. 3 n раз при i =1, 2, ..., n, получаем необходимое значение по схеме Горнера.
Реализация схемы Горнера на языке программирования С++ выглядит следующим образом:
float gorner(float k[], int n, float x)
{
float P;
P=k[n‐ 1]*pow(x, n‐ 1)+k[n‐ 2]*pow(x, n‐ 2)+k[n‐ 3]*pow(x, n‐ 3)+k[n‐
|
|
|
-4]*pow(x, n‐ 4)+k[n‐ 5]*pow(x, n‐ 5)+k[n‐ 6]*pow(x, n‐ 6)+k[n‐ 7]*pow(x, n‐
-7)+k[n‐ 8]*pow(x, n‐ 8)+k[n‐ 9]*pow(x, n‐ 9)+k[n‐ 10]*pow(x, n‐ 10);
return P;
}
|
|
|
