Таблица 3. 1 - параметры схем. Лабораторная работа 4. Решение систем линейных уравнений с комплексными коэффициентами. Таблица 3. 1 - параметры схем № п/п E1, в E2, в E3, в E4, в E5, в E6, в

Таблица 3. 1 - Параметры схем

№ п/п

E1, В

E2, В

E3, В

E4, В

E5, В

E6, В

r1, Ом

r2, Ом

r3, Ом

r4, Ом

r5, Ом

r6, Ом

1-6

7-12

13-18

19-24

25-31

 

 

Рисунок 3. 1 – Прямой ход метода Гаусса

 

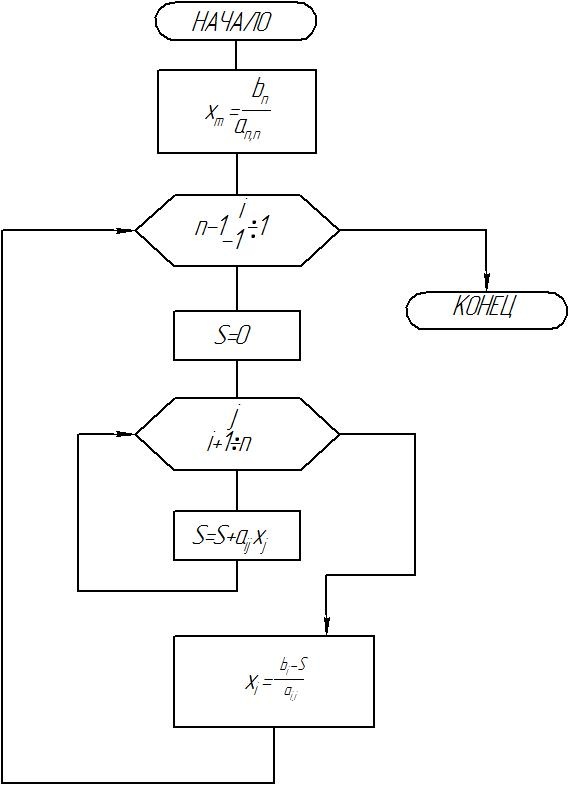
Рисунок 3. 2 – Обратный ход метода Гаусса

 

 

 

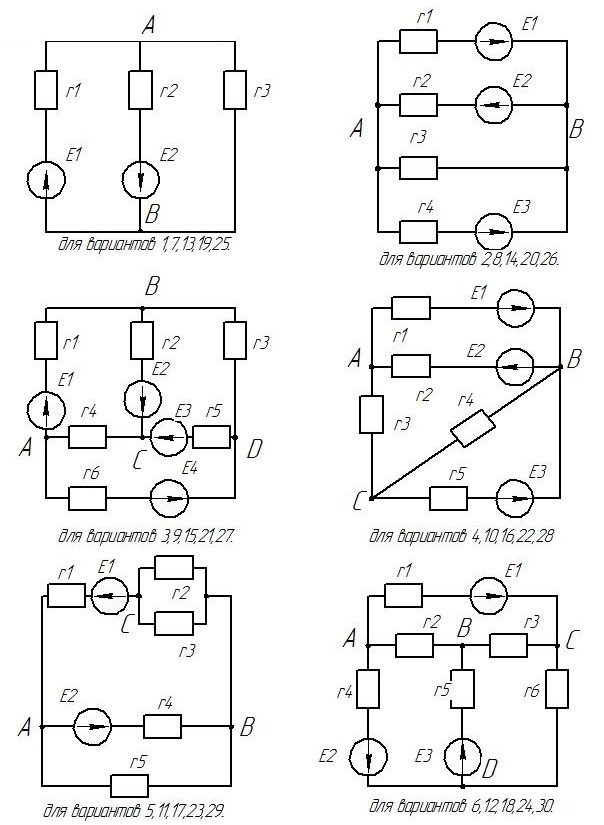
Рисунок 3. 4 – Расчетные схемы к заданию 3. 2

 

Лабораторная работа 4

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ С КОМПЛЕКСНЫМИ КОЭФФИЦИЕНТАМИ

 

Цель работы: научиться рассчитывать статические режимы в разветвленных электрических цепях.

 

4. 1 Теоретические ведомости

 

Если электрическая цепь содержит, кроме резисторов и источников постоянного тока, катушки индуктивности, конденсатора и источника переменного тока, то для расчета токов и напряжений в установившихся режимах необходимо решить систему уравнений с комплексными коэффициентами. Если при этом не учитывать нелинейность статических характеристик элементов, то получают линейную систему алгебраических уравнений, для решения которой годятся все методы, изложенные в предыдущей лабораторной работе, в том числе и метод Гаусса (см лаб. раб. 3).

Результаты работы программы: вещественные числа x1 и x2 – действительные корни квадратного уравнения либо x1 и x2 – действительная и мнимая части комплексного числа.

Комплексные числа записываются в виде a+ib, где a – действительная часть комплексного числа, b – мнимая часть комплексного числа, i – мнимая единица.

4. 2 Задание

 

Таблиця 4. 1- Параметри схем

№ п/п	L, Гн	C, мкФ	E1, В	E2, В	r1, Ом	r2, Ом	r3, Ом
1-6	0, 05
7-12	0, 08
13-18	0, 07
19-24	0, 09
25-31	0, 06

 

Рассчитать установившиеся токи в ветвях электрических цепей, приведенных на рисунке 4. 1, составив систему уравнений с помощью законов Кирхгофа. Параметры схем приведены в таблице 4. 1. Выполнить проверку результатов.

 

4. 3 Методические рекомендации

 

При выполнении работы воспользуйтесь рекомендациями и схемами алгоритмов, приведенным в предыдущей работе, заменив операции над комплексными коэффициентами вызовом соответствующих подпрограмм (процедур) и функций.

Программу дополнить следующими процедурами и функциями:

- процедурами ввода и вывода значений переменных или их массивов,

- процедурами умножения, деления и сложения двух комплексных чисел,

- процедурой изменению знака комплексного числа,

- функцией вычисления модуля комплексного числа.

 

 

Рисунок 4. 1 – Расчетные схемы к заданию 4. 2

 

Лабораторная работа 5

ОБРАЩЕНИЕ МАТРИЦ

 

Цель работы: научиться вычислять матрицу, обратную заданной с помощью ЭВМ.

 

5. 1 Теоретические сведения

 

Обращения матриц широко применяется при расчете разветвленных электрических цепей различными методами в матричной форме.

Обратной по отношению к исходной квадратной матрице называется такая квадратная матрица

 

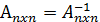
(5. 1)

 

которая, будучи умноженной на исходную дает единичную диагональную матрицу E_nxn:

 

(5. 2)

 

или в развернутой форме:

 

(5. 3)

 

Для матриц небольшого раз мера (n≤ 3) обращения чаще выполняют в ручную, используя формулу:

 

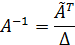
(5. 4)

 

где A - союзная матрица (матрица, составленная из алгебраических дополнений);

Δ - определитель.

При n> 3 расчеты по формуле (5. 4) становятся очень громоздкими.

Как видно из (5. 3), элементы КС-го столбца обратной матрицы Х можно определить решая систему n линейных уравнений с n неизвестными.

 

 

	(5. 5)
где КС=1, 2, ..., n.	(5. 6)

 

Таким образом, для определения всех элементов обратной матрицы необходимо решить n систем уравнений.

Этот подход часто используют при машинных расчетах. Решать системы уравнений возможно любым из известных методов, например, методом Гаусса.

Если уже существует подпрограмма решения системы уравнений, то алгоритм обращения матрицы может быть представлен схемой (рис. 5. 1)

Если подпрограмма решения систем уравнений отсутствует, то прямой ход метода Гаусса выполняют один раз над расширенной матрицей А, составленной из исходной матрицы AІ и присоединенной к ней слева единичной квадратной матрицы Е:

 

	(5. 7)
или і=1, 2, ..., n, j=1, 2, ..., 2n.	(5. 8)

В блок-схеме прямого хода (рис. 5. 1) в сравнении с алгоритмом исчезнут блоки 9 и 13, а в блоках 7 и 14 конечное значение переменной j станет равным 2n.

Обратный ход будет выполняться n раз (при КС=1, 2,..., n). При этом в схеме рисунка 3. 2 элементы вектора корней x_n, x_j и x_i необходимо заменить элементами обратной матрицы x_{n, KC}, х_{ј, KC} и x_{i, KC}, а переменные b_n и b_i - переменными a_n, _n+КС и a_i, _n+КС соответственно.

 

5. 2 Задание

 

Выполнить обращение произвольных квадратных матриц второго, третьего и четвертого порядков с контролем результата.

 

 

5. 3 Методические рекомендации

 

Оформить в виде отдельных процедурных блоков ввод, вывод, обращение матрицы и контроль результата.

Для проверки правильности решения вычислите и выведите на экран скалярное произведение исходной матрицы на полученную обратную. Если в результате получите единичную диагональную матрицу (см. уравнение (5. 3)), то результат верный.

 

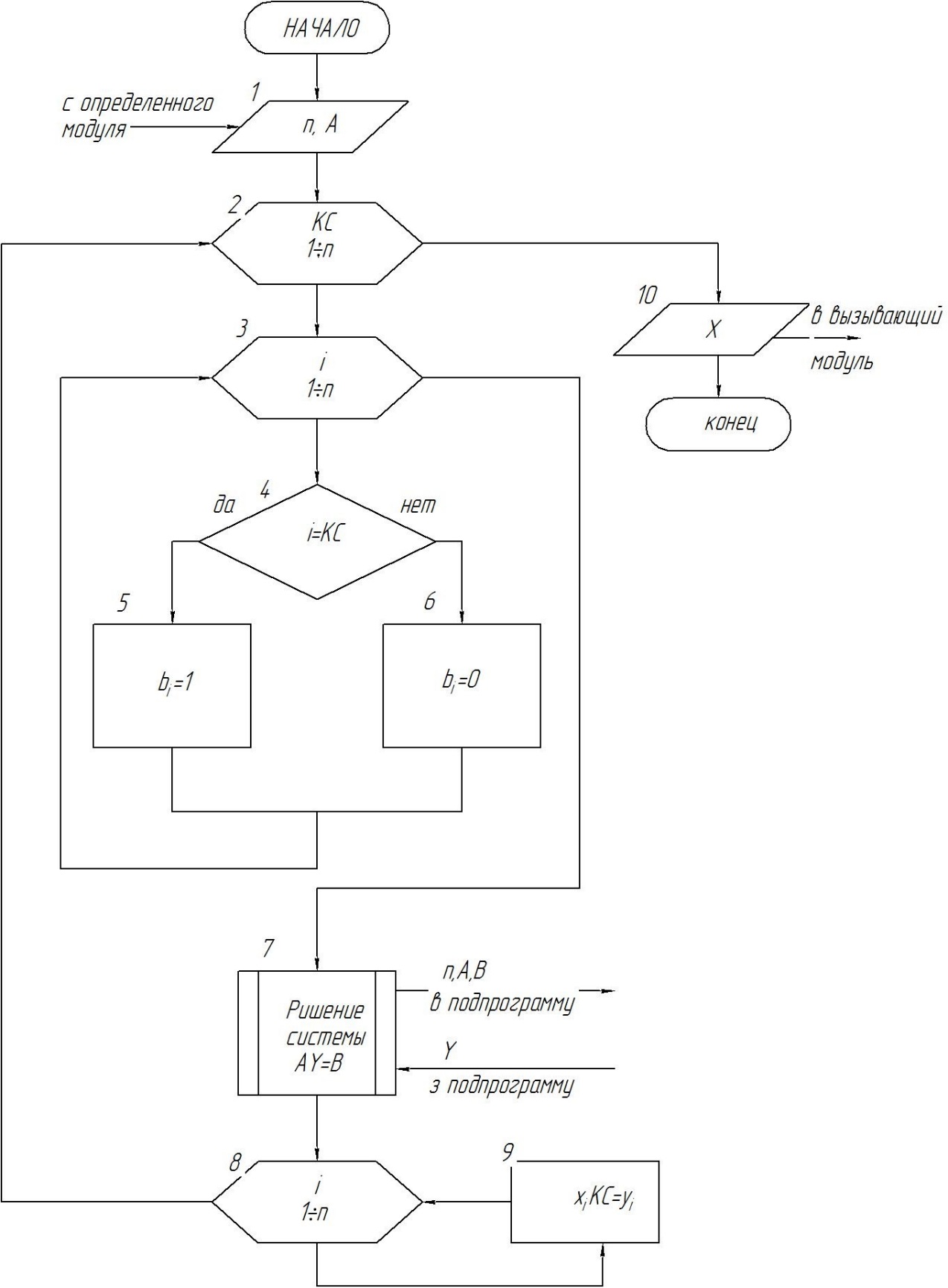Рисунок 5. 1 – Блок-схема обращения матрицы

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: