 |
Решение систем линейных уравнений с действительными коэффициентами
|
|
|
|
Цель работы: научиться вычислять на ЭВМ корни систем линейных уравнений с действительными коэффициентами.
3. 1 Теоретические сведения
Решение систем линейных уравнений используется в электротехнике и производных от нее дисциплинах при расчете статических режимов в разветвленных электрических цепях.
Система n линейных уравнений с n неизвестными имеет вид:

| (3. 1) |
Ее можно записать и в матричной форме:
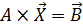
| (3. 2) |
где  - квадратная матрица коэффициентов;
- квадратная матрица коэффициентов;
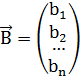 - вектор свободных членов;
- вектор свободных членов;
 - искомый вектор корней.
- искомый вектор корней.
Способы решения систем линейных уравнений делятся на две группы:
· Точные методы (метод обращения матрицы коэффициентов, правило Крамера, метод Гаусса и др. );
· Итерационные методы (Ньютона, Зейделя, простых итераций и др. ).
Если матрица А неособенная, то есть ее определитель не равен нулю, то система имеет единственное решение:

| (3. 3) |
где  - матрица, обратная матрице А.
- матрица, обратная матрице А.
Вычисления корней по формуле (3. 3) называется методом обратной матрицы коэффициентов.
Согласно правилу Крамера корни рассчитываются по формулам:

|
где  - определитель матрицы А;
- определитель матрицы А;
 - определители матриц, полученных с матрицы А путем замены ее i-го столбца вектором свободных членов.
- определители матриц, полученных с матрицы А путем замены ее i-го столбца вектором свободных членов.
Оба из вышеперечисленных методов используют на практике только при решении " вручную" систем уравнений невысокого порядка. При n> 3 эти методы очень трудоемки и не экономические.
Наиболее распространенным из точных методов является метод Гаусса.
Метод Гаусса можно разбить на два этапа:
-Прямой ход, заключающийся в последовательном исключении корней с 1-го до n-го и преобразовании матрицы коэффициентов к треугольному виду;
|
|
|
-Обратный ход, заключающийся в последовательном определении корней с n-го до 1-го из преобразованной системы уравнений.
Исключение k-го корня (k = 1, 2, ..., n-1) с i-го уравнения (i = k + 1, k + 2, ..., n) выполняется путем замены всех коэффициентов i-го уравнения разницей между бывшими коэффициентами этого уравнения и соответствующими коэффициентами i-го уравнения, умноженного на мерительный множитель:

| (3. 4) |
В результате коэффициенты i-го уравнения примут следующие значения:

| (3. 5) |
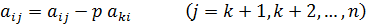
| (3. 6) |
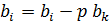
| (3. 7) |
В формулах (3. 6) и (3. 7) знак " =" используется как символ операции присваивания, в правой части используются прежние значения коэффициентов aij и bi, а в левой - новые.
При исключении корней минимальных погрешностей округления при пересчете коэффициентов можно достичь перестановкой уравнений таким образом, чтобы модули коэффициентов  при корнях, что исключаются, хk были максимально возможными. Этот этап метода Гаусса называют выбором главного элемента.
при корнях, что исключаются, хk были максимально возможными. Этот этап метода Гаусса называют выбором главного элемента.
В соответствии с вышеизложенным схема алгоритма прямого хода может иметь вид, представлен на рис. 3. 1.
В результате прямого хода система уравнений (3. 1) преобразуется к виду:

| (3. 8) |
Коэффициенты  i, j и bi системы (3. 8) не совпадают с соответствующими коэффициентами исходной системы (3. 1).
i, j и bi системы (3. 8) не совпадают с соответствующими коэффициентами исходной системы (3. 1).
С преобразованной системы корни можно рассчитать по формулам:

| (3. 9) |

| (3. 10) |
Согласно формулам блок-схеме обратного хода может иметь вид приведенный на рис. 3. 2.
Алгоритм прямого хода можно упростить, объединив квадратную матрицу коэффициентов Anx(n) и вектор - столбец свободных членов 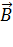 в единую матрицу ARnx(n+1), которая называется расширенной матрицей коэффициентов, в которой (n+1)-и столбец составляют элементы вектора
в единую матрицу ARnx(n+1), которая называется расширенной матрицей коэффициентов, в которой (n+1)-и столбец составляют элементы вектора 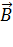 :
:

| (3. 11) |
|
|
|
При этом из блок-схемы рис. 3. 1 исчезнут блоки 9 и 13, а в блоках 7 и 14 параметр j (номер столбца) будет меняться не в n, а к n+1. В схеме рис. 3. 2 в блоках 1 и 6 переменные  и
и  придется заменить переменными
придется заменить переменными  и
и  соответственно.
соответственно.
3. 2 Задание
Рассчитать токи и напряжения в ветвях электрических цепей, приведенных на рис. 3. 4, методом законов Кирхгофа. Параметры схем приведены в таблице 3. 1. Выполнить проверку результатов.
3. 3 Методические рекомендации
Если используется язык программирования Паскаль: процесс определения корней системы уравнений удобно оформить в виде подпрограммы (процедуры) с формальными параметрами n, A, B и X, причем массив Х должен быть обязательно описан как параметр-переменная (с ключевым словом var). При использовании расширенной матрицы коэффициентов формальными параметрами процедуры будут n, A и Х.
Для описания типов массивов в разделе констант целесообразно определить максимально допустимые размеры массивов.
Для того, чтобы подпрограмма метода Гаусса была универсальной, она не должна содержать процессов ввода исходных данных и вывода результатов.
Основной модуль программы должен содержать ввод исходных данных, формирование фактических параметров для подпрограммы метода Гаусса, вызов этой подпрограммы, вывод результатов и проверку правильности решения.
Для проверки можно вычислить и вывести на экран значения функций
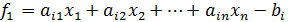 (i=1, 2, …, n). (i=1, 2, …, n).
| (3. 12) |
При правильном решении эти значения должны быть близки к нулю.
Вывод матрицы и контроль результатов можно оформить в виде отдельных подпрограмм.
|
|
|


