 |
Лабораторная работа 2. Простейшие операции с матрицами. К наиболее легко вычислительных норм относятся следующие три Нормы: (2. 7) максимальная сумма модулей элементов матрицы по строкам; (2. 8) максимальная сумма модулей элементов матрицы по
|
|
|
|
Лабораторная работа 2
ПРОСТЕЙШИЕ ОПЕРАЦИИ С МАТРИЦАМИ
Цель работы: научиться вычислять сумму, разницу и скалярное произведение матриц, транспонировать их и определять нормы матриц.
2. 1 Теоретические сведения
В электротехнических расчетах часто используются матрицы и векторы (вектором называют матрицу - строку или матрицу - столбец). В данной лабораторной работе рассмотрены простейшие операции над матрицами: сумма, разность, умножение, транспонирование, вычисление некоторых норм. Более сложные операции будут рассмотрены позже.
2. 1. 1 Сумма и разность двух матриц
Суммой двух матриц одного и того же размера
| A+B=[аi, j]+[bi, j] (i=1, 2, …, m; j=1, 2, …, n) |
называется матрица C=[Ci, j] того же размера, элементы которой равны суммам соответствующих элементов матриц A і B:
Ci, j=  i, j+bi, j
| (2. 1) |
Разница матриц определяется аналогично сумме, только у элементов матрицы, вычитается, знак меняется на противоположный, то есть элементы матрицы С = В - А вычисляются по формуле:
| Ci, j=bi, j-ai, j (i=1, 2, …, m; j=1, 2, …, n) | (2. 2) |
2. 1. 2 Скалярное произведение матриц и сведение их в степень
Скалярным произведением матрицы А размером m´ k на матрицу В размером k´ n назеваться матрица С размером m´ n, элементы которой вычисляются по формуле:
| (2. 3) |
Отметим, что матрица С=А´ В определена только тогда, когда число столбцов матрицы А равно числу строк матрицы В.
Для скалярного произведения матриц несправедливый переместительный закон, то есть АВ≠ ВА.
Частные случаи умножения матриц является умножение матрицы А размером m´ k на вектор - столбец 
, состоящий из k элементов, и вектора строки 
, состоящий из k элементов, на матрицуВ размером k´ n.
|
|
|
В первом случае результатом будет вектор - столбец с элементами (і=1, 2,..., m),
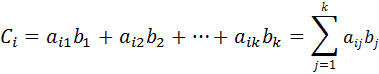
| (2. 4) |
а во втором случае - вектор - строка с элементами
| (2. 5) |
Согласно понятия о скалярном произведении матриц в целую положительную степень k можно возвести только квадратную матрицу
 Аk=((АА)× А)…× А)
k- сомножителей
| (2. 6) |
2. 1. 3 Транспонирование матриц
Если в матрице А размером m´ n заменить строки соответствующими столбцами, то получим матрицу А 
размером n´ m, что называется транспонированной по отношению к матрице А.
Таким образом:
(i=1, 2, …, n; j=1, 2, …, m).
2. 1. 4 Нормы матриц
Под нормой матрицы A=[aij] разумеется действительное число ||A||, удовлетворяющая следующим условиям:
||A||≥ 0 (причём ||A=0|| только при А=[0]),
||aA||=|a|*||A||, где a - действительное число (причём ||-A||=||A||),
||A||+||B||≥ ||A+B||,
||AB||£ ||A||*||B||,
||A-B||≥
B||-||A
. К наиболее легко вычислительных норм относятся следующие три нормы: (2. 7) максимальная сумма модулей элементов матрицы по строкам; (2. 8) максимальная сумма модулей элементов матрицы по столбцам; (2. 9) корень квадратный из суммы квадратов модулей всех элементов матрицы. 2. 2 Задание Выполнить операции над матрицами в соответствии с выражениями, которые приведены в таблице 2. 1. Повторяющиеся действия оформить в виде отдельных процедур: , , , Таблица 2. 1- Исходные данные к лабораторной работе №2 № п/п Задание проверить соотношение: ||A+C||1£ ||A||1+||C||1 ||A*B||1£ ||A||1*||B||1 ||A-C||1³ | ||C||1-||A||1 | ||A+C||2£ ||A||2+||C||2 Продолжение таблицы 2. 1 ||A*B||2£ ||A||2*||B||2 ||A-C||2³ | ||C||2-||A||2 | ||A+C||3£ ||A||3+||C||3 ||A*B||3£ ||A||3*||B||3 ||A-C||3³ | ||C||3-||A||3 | вычислить: K=A+C+BT K=B(A+C)+D K=(A-C)*(D*B) K=BT-A-C K=B*A*B L=||A+C||1+||B||1 L=||A||1+||B||2+||C||1 K=C*D+A+C K=B*C*D ||A||1 ||AT||1 ||B||1 ||BT||1 K=D*CT*A K=D-B*C-B*A K=AT+CT+B K=(A-C)*B K=C*D-A-C 1. 3 Методические рекомендации Чтобы вычислить сумму элементов массива дан массив X, состоящий из N элементов. Переменной S присваивается значение равное нулю, затем последовательно суммируются элементы массива X. Блок-схема алгоритма расчета суммы приведена на рис. 2. 1. Рисунок 2. 1 Алгоритм вычисления суммы элементов массива Дан массив X, состоящий из N элементов. Найти произведение элементов этого массива. Решение этой задачи сводится к тому, что значение переменной Р, в которую предварительно была записана единица, последовательно умножается на значение i–го элемента массива. Блок-схема алгоритма приведена на рис. 2. 2. Рисунок 2. 2 Вычисление произведения элементов массива Для того, чтобы транспонировать заданную матрицу Aij присвоим переменную N строкам матрицы, а M – столбцы. Матрицу Bji используем в качестве выходного параметра, т. е. результата поставленной задачи. В итоге значения строк и столбцов меняются местами. Блок-схема транспонирования матрицы приведена на рис. 2. 3. Рисунок 2. 3 Блок схема транспонированной матрицы Дан массив X, состоящий из n элементов. Найти максимальный элемент массива и номер, под которым он хранится в массиве. Алгоритм решения задачи следующий. Пусть в переменной с именем Max хранится значение максимального элемента массива, а в переменной с именем Nmax – его номер. Предположим, что нулевой элемент массива является максимальным и запишем его в переменную Max, а в Nmax – его номер (то есть ноль). Затем все элементы, начиная с первого, сравниваем в цикле с максимальным. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Max, а в переменную Nmax – текущее значение индекса i. Процесс определения максимального элемента в массиве приведен в таблице 5. 3 и изображен при помощи блок-схемы на рис. 2. 4. Рисунок 2. 4 Поиск максимального элемента и его номера в массиве
|
|
|
Лабораторная работа 3
|
|
|
