 |
Лабораторная работа 6. Вычисления определителей матриц. Для вычисления определителя можно преобразовать исходную матрицу в треугольную форму с помощью прямого хода метода Гаусса и рассчитать произведение ее диагональных элементов
|
|
|
|
Лабораторная работа 6
ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ
Цель работы: научиться вычислять определители матриц с помощью ЭВМ.
6. 1 Теоретические сведения
Для вычисления определителя можно преобразовать исходную матрицу в треугольную форму с помощью прямого хода метода Гаусса и рассчитать произведение ее диагональных элементов.
Программу на C++, решающую системы линейных уравнений методом Крамера, удобно реализовать с функциями для вычисления определителя системы и определителя при неизвестных (рис 6. 1). Тело каждой функции содержит и запись математических операций вычисления определителей.
Для вычисления определителей матриц методом Крамера (рис. 6. 1) в качестве исходных данных используем квадратную матрицу Aij и вектор свободных коэффициентов Bij. В вызове Kramer функций указываются уже фактические параметры - массивы, хранящие перечисленные данные, но уже состоящие из значений, введённых пользователем. В результате получим решение СЛАУ.
Рисунок 6. 1 – Алгоритм выполнения программы
Если в схеме прямого хода используется перестановка строк, то необходимо учесть, что одна такая перестановка меняет знак определителя на противоположный.
6. 2 Задание
Решить системы уравнений, приведенные в таблице 6. 1, методом Крамера. Выполнить проверку результата.
Таблица 6. 1 – Исходные данные
| № п/п | Система уравнений |
| 1, 2 | 3. 14 x1-2. 2x2+1. 17x3=1. 27 -2. 12x1+1. 32x2-2. 45x3=2. 13 1. 17x1-2. 45x2+1. 18x3=3. 14 |
| 3, 4 | 2. 45x1+1. 75x2 –3. 24x3=1. 23 1. 75x1-1. 16x2 +2. 18x3=3. 43 -3. 24x1+2. 18x2 –1. 85x3=-0. 16 |
| 5, 6 | 1. 65x1-2. 27x2 +0. 18x3=2. 25 -2. 27x1+1. 73x2 –0. 46x3=0. 93 0. 18 x1-0. 46x2 +2. 16x3=1. 33 |
| 7, 8 | 3. 23x1+1. 62x2 +0. 65x3=1. 28 1. 62x1-2. 33x2 –1. 43x3=0. 87 0. 65x1-1. 43x2 +2. 18x3=-2. 87 |
| 9, 10 | 0. 93x1+1. 42x2 -2. 55x3=2. 48 1. 42x1-2. 87x2 +2. 36x3=-0. 75 -2. 55x1+2. 36x2 –1. 44x3=1. 83 |
| 11, 12 | 1. 42 x1-2. 15x2 +1. 07x3=2. 48 -2. 15x1+0. 76x2-2. 18x3=1. 15 1. 07x1-2. 18x2+1. 23x3=0. 88 |
| 13, 14 | 2. 23x1-0. 71x2 +0. 63x3=1. 28 -0. 71x1+1. 45x2 –1. 34x3=0. 64 0. 63 x1-1. 34x2 +0. 77x3=-0. 87 |
| 15, 16 | 1. 63x1+1. 27x2 –0. 84x3=1. 51 1. 27x1+0. 65x2 +1. 27x3=-0. 63 -0. 84x1+1. 27x2 –1. 21x3=2. 15 |
| 17, 18 | 0. 78x1+1. 08x2 –1. 35x3=0. 57 1. 08x1-1. 28x2 +0. 37x3=1. 27 -1. 35x1+0. 37x2 +2. 86x3=0. 47 |
| 19, 20 | 0. 83x1+2. 18x2 –1. 73x3=0. 28 2. 18 x1-1. 41x2 +1. 03x3=-1. 18 -1. 73x1+1. 03x2 +2. 27x3=0. 72 |
| 21, 22 | 2. 74x1-1. 18x2 +1. 23x3=0. 16 -1. 18x1+1. 71x2 –0. 52x3=1. 81 1. 23x1-0. 52x2 +0. 62x3=-1. 25 |
| 23, 24 | 1. 35x1-0. 72x2 +1. 81x3=0. 88 -0. 72x1+1. 45x2 –2. 18x3=1. 72 1. 38x1-2. 18x2 +0. 93x3=-0. 72 |
Лабораторная работа 7
|
|
|
ОТДЕЛЕНИЕ КОРНЕЙ ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
Цель работы: повторить построение графиков функций и научиться отделять корни трансцендентных уравнений.
7. 1 Теоретические сведения.
Уравнение:
| f(x)=0 | (7. 1) |
называется трансцендентным, если оно содержит тригонометрические или другие специальные функции (экспоненциальные, логарифмические и др. ) переменной х.
Трансцендентные уравнения имеют неопределенное число решений, могут иметь бесконечное число решений.
Если рассмотренные уравнения не имеют аналитического решения, то их решают итерационными методами. Первым этапом решения такой задачи является отделение корней, т. е. определение интервала существования корня и его начального приближения.
Для отделения действительных корней трансцендентных уравнений часто весьма приблизительно построить график функции f(х) или, преобразовав исходное уравнение f(х)=0 к виду j1(x)=j2(х), построить графики двух функций j1(x) и j2(х) и определить примерно область точки их пересечения. Искомый интервал существования корня [a, b] должен удовлетворять условию
| f(a)× f(b)< 0. | (7. 2) |
7. 2 Задание.
Отделить первый положительный корень трансцендентного уравнения, приведенного в таблице 7. 1, графическим методом.
7. 3 Методические рекомендации
|
|
|
Левую границу поиска хн выберите равной нулю (если f(0) существует) или близком к нему положительному значению, например, 0, 01 или 0, 1. Правая граница поиска хк произвольная и зависит от функции f(х). Для уравнений таблицы ее не следует принимать более 5. Первоначальное значение шага поиска Δ х выберите таким, чтобы на интервале поиска рассчитывалось не более 20 значений функции. Выведите их на экран.
Если в области поиска не окажется изменение знака функции f(х), уменьшите Δ х и (или) увеличьте хк и повторите вычисления.
Для графика определите (программно или визуально) максимальное и минимальное значение функции на основании этой информации определите пределы графика и постройте его.
Используйте график не только для отделения корня, но и для выбора наиболее удачного метода его уточнения.
Функцию f(х) определите как функцию пользователя.
7. 3. 1 Метод касательных.
В одной из точек интервала [a, b], пусть это будет точка с, проведем касательную (рис 7. 1). Запишем уравнение этой прямой:
y=k*x+m
Так как эта прямая является касательной, и она проходит через точку (c, f(c)), то k=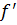 
(c).
Следовательно,
y= 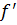(x)*x+m, f(c)= 
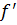*c+m, m=f(c)-c* (c),
y= 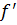(c)*x+f(c)-c* 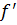(c), y= 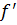(c)*(x-c)+f(c).
Найдем точку пересечения касательной с осью х:
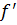(с)*(x-c)+f(c)=0, x=c- 
Рисунок 7. 1 - Графическая интерпретация метода касательных
Если ∣ f(x)∣ < ε , то точность достигнута, и точка х – решение (рис 7. 2); иначе необходимо переменной с присвоить значение х и провести касательную через новую точку с; так продолжать до тех пор, пока ∣ f(x)∣ не станет меньше ε.
Рисунок 7. 2 Алгоритм метода касательных
Осталось решить вопрос, что выбрать в качестве точки начального приближения c. В этой точке должны совпадать знаки функции и ее второй производной. А так как нами было сделано допущение, что вторая и первая производные не меняют знак, то можно проверить условие на обоих концах интервала и в качестве начального приближения взять ту точку, где это условие выполняется.
7. 3. 2 Метод хорд.
Этот заключается в том, что очередное приближение берем не в середине отрезка, а в точке пересечения с осью Х (рис. 7. 3) прямой, соединяющей точки (a, f (a)) и (b, f (b)).
|
|
|
Запишем уравнение прямой, проходящей через точки с координатами (a, f (a)) и (b, f (b)):
| (7. 3) |
Прямая, заданная уравнением, пересекает ось Х при условии y=0. Найдем точку пересечения хорды с осью Х:
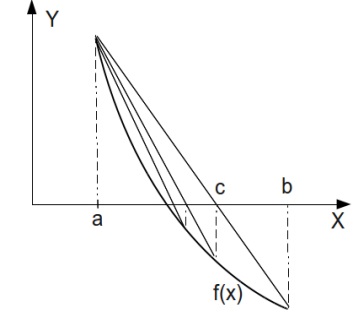
Рисунок 7. 3 Графическая интерпретация метода хорд
Далее необходимо вычислить значение функции в точке с. Это и будет корень уравнения. Блок-схема метода представлена на рис. 7. 4.
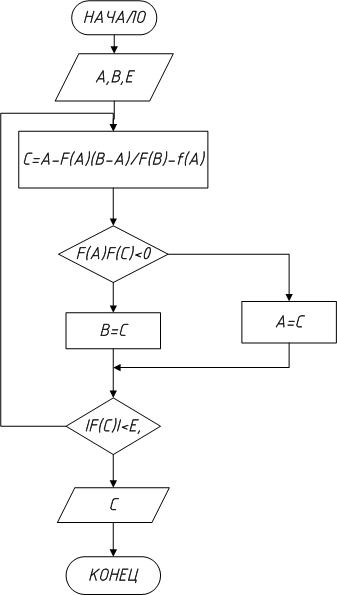
Рисунок 7. 4 Алгоритм метода хорд
7. 3. 3 Метод бисекций.
Пусть был выбран интервал изоляции [a, b] (рис. 7. 5). Примем за первое приближение корня точку с, которая является серединой отрезка [a, b] Далее находим точку c=(a+b)/2 и значение f(c). Если f(a)*f(c)< 0, то корень лежит на интервале [a, c], иначе [c, b]. Если величина интервала меньше заданной точности, то ищем корень с более приближенной точностью.
Рисунок 7. 5 Графическая интерпретация метода бисекций.
Блок-схема алгоритма решения уравнения приведена на рис. 7. 6.
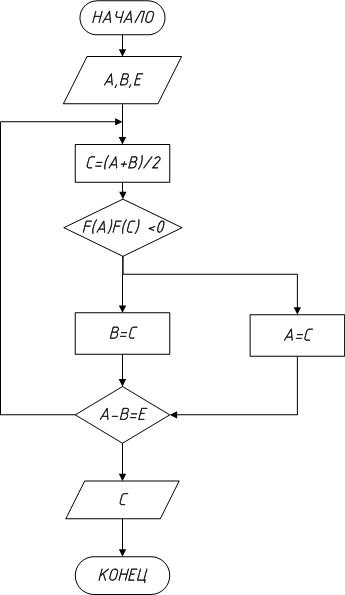
Рисунок 7. 6 Алгоритм решения методом бисекций
Таблица 7. 1 – Задания к лабораторной работе №7
| № п/п | Уравнение | Метод решения |
| 2sin(x+p/3)-0. 5x2+1=0 | Касательных | |
| cos(x+0. 3)-x2=0 | Касательных | |
| tg3x-x+1=0 | Касательных |
| Продолжение таблицы 7. 1 | ||
| 2arctg x –x+3=0 | Касательных | |
| (x+3)cos x-1=0 | Касательных | |
| tg(0. 58x+0. 1)-x2=0 | Касательных | |
| Хорд | |
| Бисекций | |
| 2ln x-x/2+1=0 | Бисекций | |
| ln x –1/ x2=0 | Бисекций | |
| 4. 3sin 4x-3. 5x=0 | Хорд | |
| 2x-2(x-2)-1=0 | Бисекций | |
| cos(15. 6x)+0. 5=0 | Бисекций | |
| 0. 5x+1-(x-2)2=0 | Касательных | |
| 3(x-1)-2-x=0 | Хорд | |
| x2cos 2x+1=0 | Хорд | |
| x2-2(x-1)=0 | Касательных | |
| 5sinx-x=0 | Бисекций | |
| arctg(x-1)+2x=0 | Хорд | |
| (x-2)2-2x=0 | Касательных | |
| 2ex-5x-2=0 | Касательных | |
| cos(x+0. 5)-x3=0 | Касательных | |
| x2-20sin x=0 | Хорд | |
| 2arctg x-1/2x3=0 | Хорд | |
| e-x+x2-2=0 | Хорд | |
|
|
|
