Лабораторная работа 13. Аппроксимация методом наименьших квадратов. Аппроксимация – это приближенное выражение каких-либо величин через другие, более простые величины

Лабораторная работа 13

Аппроксимация методом наименьших квадратов

 

Цель работы: научиться описывать табличные функции аналитическими выражениями.

 

13. 1 Теоритические сведения

 

Аппроксимация – это приближенное выражение каких-либо величин через другие, более простые величины.

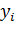Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных  и принимает наименьшее значение. То есть, при заданных данных сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей.

Для упрощения изложения рассмотрим сначала случай линейной функции одного аргумента (рис. 13. 1). Пусть из опыта получены точки ,  и ,  и .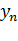

 

 

Рисунок 13. 1 – Линейная функция одного аргумента

 

Чем меньше числа по абсолютной величине, тем лучше подобрана прямая. В качестве характеристики точность подбора прямой можно принять сумму квадратов.

Аппроксимация табличной функции:

yi = f(xi)

(13. 1)

 

i=1, 2, …, n

(13. 2)

 

Метод наименьших квадратов состоит в определении параметров некоторой аналитической функции F(x), обеспечивающий минимизацию функционала (Ф):

(13. 3)

Чтобы при найденных  и функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции была положительно определенной.

Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.

Если в качестве аппроксимирующей функции выбран ступенчатый многочлен:

(13. 4)

то задача сводится к определению вектора коэффициентов    путем решения системы линейных уравнений (k+1) -го порядка:

 

(13. 5)

где:

	(13. 6)
	(13. 7)
m=0, 1, …, k	(13. 8)

 

После преобразований система (13. 5) принимает вид:

 

(13. 9)

 

Из системы (13. 9) видно, что элементы матрицы коэффициентов А и вектора свободных членов  можно описать формулами

 

(13. 10)

 

После определения коэффициентов систему (13. 9) можно решить любым из известных методов, например методом Гаусса и получаем формулы для нахождения коэффициентов по методу наименьших квадратов.

Аппроксимацию методом наименьших квадратов часто применяют для сглаживания табличных функций, полученных в результате эксперимента, а также для уменьшения объема информации о табличные функции при невысоких требованиях к точности расчетов.

13. 2 Задание.

 

Аппроксимировать табличную функцию, приведенную в табл. 12 ступенчатым многочленом k-го порядка методом наименьших квадратов. Для нечетных вариантов k = 3, для четных k = 2. Вычислить значение функционала, что минимизируется. Проиллюстрировать результаты графиками. Выполнить программу дважды при разном количестве табличных точек (n=9 и n=5). Оценить влияние количества точек на точность аппроксимации.

 

13. 3 Методические рекомендации.

 

При использовании для решения системы уравнений (13. 9) стандартных подпрограмм необходимо согласовать индексы стандартной системы уравнений (не содержит коэффициентов с нулевыми индексами) и системы (13. 9). Согласование состоит в изменении формул. (13. 10).

Лабораторная работа 14

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

 

Цель работы: научиться вычислять на ЭВМ определенные интегралы от функций, заданных таблично и аналитически.

 

14. 1 Теоретические сведения

 

Задачи, в которых нужно вычисления интегралов, возникают практически во всех областях прикладной математики.

Численные методы интегрирования основаны на том, что интервал [a, b] разбивают на участки, на каждом из которых кривая, описываемая подiнтегральною функцией f(x), заменяется некоторой другой кривой, для которой вычисления интеграла выполняется достаточно простыми формулами, а затем все площади суммируются.

При замене подинтегральной функции полиномами, что интерполируют, получают так называемые. квадратурные формулы. Квадратурные формулы для равноудаленных узлов интерполяции называют формулами Ньютона-Котеса.

В зависимости от степени полинома интерполюе, различают методы прямоугольников, трапеций и квадратичной трапеций, или метод Симпсона.

Основные формулы и показатели, характеризующие эти методы при разбивке интервала интегрирования на равные отрезки, приведены в табл. 14. 1, где приняты следующие обозначения:

 

n - число участков разбивки,

- шаг интергрирования,

(14. 1)

 

Погрешность методов определяется величиной интеграла от остаточного члена интерполяционного полинома. В формулах для оценки погрешности Mi - максимальное значение n-й производной   на интервале [a, b].

 

Таблица 14. 1 – задание к лабораторной работе №14

Название метода	Степень полинома, который интерполирует		Погрешность
Прямоугольников

 

 

Продолжение таблицы 14. 1
Трапеций
Симпсона

 

При использовании метода Симпсона число участков разбивки обязательно должно быть четным (n=2k) и все участки должны быть одинаковыми (h=const). При неравномерной разбивке интервала интегрирования используют обычно методы прямоугольников и трапеций, для которых формулы численного интегрирования в этом случае приобретают вид:

 

· по методу прямоугольников,

	(14. 2)

Метод прямоугольников – метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, тоесть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближенном вычислении площади под графиком суммированием площадей конечного числа прямугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота – значением подынтегральной функции в этих узлах.

Рисунок 14. 1 - Метод прямоугольников

 

· по методу трапеций,

(14. 3)

Метод трапеций – метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть на линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями

 

Рисунок 14. 2 - Метод трапеций

 

Для обеспечения заданной точности интегрирования часто используют алгоритмы с автоматическим выбором шага (АВШ), в которых используют такой прием. Вычисляют значение интеграла одним из рассмотренных методов с некоторым начальным шагом h, а затем повторяют эти же вычисления с половинным шагом . Если определится, что:

 

(14. 4)

 

где - допустимая ошибка интегрирования, то вычислительный процесс прекращают, в противном случае подают к дальнейшему дробления шага. Полученное таким методом приближенное значение интеграла можно уточнить, используя экстраполяционный переход к лимита, который был предложен Ричардсоном:

 

(14. 5)

где:

(14. 1)

 

14. 2 Задание

14. 2. 1 Интегрирование табличных функций

 

Рассчитать определенный интеграл от табличной функции, заданной в табл. 14. 2. Непарные варианты используют метод трапеций при неравномерной разбивке интервала интегрирования и метод Симпсона - при ривномирной, четные варианты в аналогичных ситуациях используют метод прямоугольников и метод трапеций соответственно.

 

14. 2. 2 Интегрирование функций, заданных аналитически

 

Вычислить определенный интеграл

 

 

для функции, приведенной в табл. 14. 2, на заданном интервале [a, b] с заданной точностью , используя указанный в таблице метод с автоматическим выбором шага.

14. 3 Методические рекомендации

 

Для визуального контроля результата постройте график подынтегральной функции и нанесите на него прямую, параллельную оси абсцисс, на уровне:

 

 

При правильном решении площадь, ограниченная подынтегральной кривой и прямыми х=а, x=b и y=0, будет примерно равна площади прямоугольника, ограниченного отрезками прямых y=yсp, x=a, x=b, y=0.

 

Таблица 14. 2 – Исходные данные к лабораторной работе №14

№ п/п	Метод		f(x)	a	b	Параметры
	Прямоугольников	10-5				=0, 182
	Симпсона	10-3
	Трапеций	10-4				c=0, 953 d=2, 295
	Прямоугольников	10-2

 

Продолжение таблицы 14. 1
						7
	Трапеций	10-6				c=3, 18 d=-1, 37
	Симпсона	10-3
	Прямоугольников	10-2				m=3
	Трапеций	10-4
	То же	10-5				c=1, 21
	Симпсона	10-3
	Трапеций	10-2				c=8, 53 d=0, 524
	Прямоугольников	10-4
	Симпсона	10-5				c=0, 732
	Трапеций	10-3
	Прямоугольников	10-4				c=3, 76 d=8, 39
	Трапеций	10-2
	Симпсона	10-6				c=4, 18
	Трапеций	10-3
	То же	10-2				c=0, 874
	Прямоугольников	10-4
	Симпсона	10-5				c=2
	Трапеций	10-3
	Прямоугольников	10-2
	Симпсона	10-4
	То же	10-5				c=0, 5
	Трапеций	10-3

 

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: