Лабораторная работа 15. Гармонический анализ и синтез периодических функций. Функция времени f(t) называется периодической, если к ней справедливо условие:

Лабораторная работа 15

Гармонический анализ и синтез периодических функций

 

Цель работы: научиться определять гармоничный состав периодических функций.

15. 1 Теоретические сведения

 

Функция времени f(t) называется периодической, если к ней справедливо условие:

 

(15. 1)

где Т - период.

 

Гармонический анализ периодических функций состоит в определении коэффициентов  и ,  ряда Фурье:

 

(15. 2)

где круговая частота первой гармоники;

k - порядковый номер гармоники.

Ограничившись в формуле (15. 2) некоторой конечным количеством гармоник m, получают аппроксимирующий гармоничный многочлен Q_m(t):

 

(15. 3)

 

Коэффициенты Фурье определяются выражениями:

 

(15. 4)

 

Используя для численного интегрирования в формулах (15. 4) метод прямоугольников при разбивке интервала интегрирования [0, T] на n равных отрезков, получим:

 

k=1, 2, …, m,	(15. 5)
	(15. 6)
	(15. 7)
	(15. 8)

При

n=2k

(15. 10)

 

Гармоничным синтезом называется получения периодической функции путем суммирования ее гармонических составляющих по формуле (15. 3).

15. 2 Задание

 

Рассчитать коэффициенты интерполирующего тригонометрического многочлена, что аппроксимирующую табличную функцию из таблицы, заданную в точках

 

при

 

Построить график функции, которая интерполирует, и нанести на него исходную табличную функцию в виде решетки.

15. 3 Методические рекомендации

Все вышеперечисленные функции являются периодическими функциями с периодом 2π . Каждый член тригонометрического ряда Фурье является периодической функцией с периодом 2π. Поэтому и любая частичная сумма ряда Фурье 2π - периодична.

Отсюда следует, что если ряд Фурье сходится на отрезке [-π; π ], то он сходится на всей числовой прямой и его сумма, будучи пределом последовательности периодических частичных сумм, является периодической функцией с периодом 2π.

Вышеупомянутое свойство видно на графике внизу (рис. 15. 1): здесь график суммы ряда для функции f(x) = x. Вне отрезка [-π; π ] сумма ряда является периодическим продолжением данной функции, то есть график функции бесконечно повторяется справа и слева.

 

 

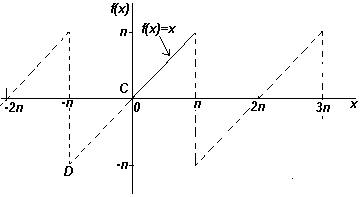
Рисунок 15. 1 - Периодическая функция ряда Фурье

 

Для наглядности плотность точек на графике аппроксимирующей функции должна в 5-10 раз превышать плотность точек, разбивают период на отрезки для численного интегрирования.

Проследите, как влияет количество гармоник m при заданном количестве отрезков разбиения n на точность аппроксимации.

Таблица 15. 1 – Исходные данные к лабораторной работе №15

№ п/п.	Табличные значения функции
	1. 00, 1. 803, 3. 085, 4. 776, 6. 434, 7. 347, 7. 027, 5. 652, 3. 897, 2. 381, 1. 347, 7. 422, 0. 419, 0. 256, 0. 176, 0. 142, 0. 136, 0. 155, 0. 209, 0. 324, 0. 554
	7. 38, 6. 76, 5. 22, 3. 47, 2. 07, 1. 16, 0. 64, 0. 36, 0. 23, 0. 16, 0. 13, 0. 13, 0. 16, 0. 23, 0. 37, 0. 64, 1. 16, 2. 08, 3. 48, 5. 22, 6. 76
	-1. 24, -1. 17, -1. 08, -0. 96, -0. 84, -0. 79, -0. 8, -0. 9, -1. 1, -1. 21, -1. 02, -1. 28, -1. 32, -1. 34, -1. 36, -1. 37, -1. 37, -1. 36, -1. 35, -1. 33, -1. 30
	-3. 0, -3. 58, -4. 12, -4. 56, -4. 86, -4. 99, -4. 94, -4. 73, -4. 36, -3. 86, -3. 30, -2. 7, -2. 13, -1. 64, -1. 26, -1. 05, -1. 00, -1. 13, -1. 43, -1. 87, -2. 43
	1. 0, 1. 05, 90. 6, 520. 4, 1714. 7, 2915. 0, 2439. 2, 1020. 6, 230. 7, 32. 17, 3. 29, 0. 3, 0. 03, 0. 004, 0. 001, 0. 0003, 0. 0006, 0. 002, 0. 01, 0. 09, 0. 9
	2980. 1, 2089. 3, 742. 4, 146. 6, 18. 6, 1. 8, 0. 16, 0. 02, 0. 003, 0. 001, 0. 001, 0. 001, 0. 002, 0. 003, 0. 018, 0. 9, 1. 22, 18. 6, 146. 6, 742. 5, 2089. 7
	1. 0, 1. 34, 1. 75, 2. 18, 2. 53, 2. 71, 2. 65, 2. 37, 1. 97, 1. 54, 1. 16, 0. 86, 0. 64, 0. 5, 0. 42, 0. 37, 0. 36, 0. 39, 0. 45, 0. 56, 0. 74
	2. 71, 2. 6, 2. 28, 1. 86, 1. 44, 1. 07, 0. 8, 0. 46, 0. 42, 0. 4, 0. 37, 0. 37, 0. 4, 0. 48, 0. 6, 0. 8, 1. 07, 1. 44, 1. 86, 2. 28, 2. 6
	-1. 32, -1. 28, -1. 26, -1. 24, -1. 25, -1. 25, -1. 25, -1. 26, -1. 27, -1. 29, -1. 29, -1. 33, -1. 34, -1. 37, -1. 37, -1. 37, -1. 37, -1. 36, -1. 36, -1. 35, -1. 34

 

Продолжение таблицы 15. 1
	-4. 0, -4. 2, -4. 5, -4. 7, -4. 9, -5. 0, -4. 9, -4. 8, -4. 6, -4. 4, -4. 1, -3. 8, -3. 5, -3. 1, -3. 0, -3. 0, -3. 0, -3. 1, -3. 2, -3. 4, -3. 7
	1. 0, 2. 4, 5. 4, 10. 4, 16. 3, 19. 9, 18. 6, 13. 4, 7. 7, 3. 6, 1. 6, 0. 64, 0. 27, 0. 13, 0. 07, 0. 05, 0. 05, 0. 06, 0. 09, 0. 18, 0. 4
	20. 0, 17. 5, 11. 9, 6. 4, 2. 9, 1. 2, 0. 5, 0. 2, 0. 1, 0. 06, 0. 05, 0. 05, 0. 06, 0. 1, 0. 5, 1. 0, 1. 2, 2. 9, 6. 4, 11. 9, 17. 5
	-1. 1, -0. 8, -0. 3, 0. 3, 0. 7, 0. 8, 0. 7, 0. 5, 0. 04, -0. 6, -0. 9, 1. 1, -1. 27, -1. 32, -1. 35, -1. 37, -1. 37, -1. 36, -1. 34, -1. 3, -1. 2
	-2. 0, -2. 8, -3. 7, -4. 3, -4. 7, -4. 9, -4. 9, -4. 5, -4. 1, -3. 3, -2. 4, -1. 5, -0. 6, -0. 04, 0. 6, 0. 02, 0. 99, 0. 79, 0. 34, 0. 3, -1. 1
	1. 1, 3. 2, 9. 5, 22. 8, 41. 4, 53. 9, 49. 4, 31. 9, 15. 2, 5. 7, 1. 8, 0. 55, 0. 17, 0. 06, 0. 03, 0. 02, 0. 01, 0. 02, 0. 04, 0. 1, 0. 3
	-0. 78, -1. 22, -1. 34, -1. 39, -1. 42, -1. 43, -1. 42, -1. 41, -1. 37, -1. 3, -1. 1, -0. 1, 1. 1, 1. 2, 1. 33, 1. 36, 1. 37, 1. 35, 1. 3, 1. 17, 0. 65
	54. 5, 45. 7, 27. 2, 12. 1, 4. 3, 1. 3, 0. 4, 0. 13, 0. 05, 0. 03, 0. 02, 0. 02, 0. 03, 0. 05, 0. 13, 0. 41, 1. 3, 4. 3, 12. 1, 21. 2, 45. 7
	-0. 78, 0. 18, 0. 89, 1. 13, 1. 21, 1. 24, 1. 23, 1. 18, 1. 04, 0. 63, -0. 38, -1. 01, -1. 22, -1. 3, -1. 35, -1. 36, -1. 37, -1. 36, -1. 33, -1. 27, -1. 1
	-1. 0, -2. 1, 3. 2, -4. 1, -4. 7, -4. 9, -4. 8, -4. 4, -3. 7, -2. 7, -1. 6, -0. 4, 0. 7, 1. 7, 2. 4, 2. 9, 3. 0, 2. 7, 2. 1, 1. 2, 0. 2
	1. 0, 4. 36, 16. 7, 49. 8, 105. 0, 146. 3, 130. 9, 75. 9, 30. 0, 8. 75, 2. 1, 0. 47, 0. 11, 0. 03, 0. 01, 0. 007, 0. 006, 0. 009, 0. 02, 0. 05, 0. 2
	148. 4, 118. 8, 62. 6, 25. 5, 6. 21, 1. 45, 0. 33, 0. 08, 0. 02, 0. 01, 0. 007, 0. 007, 0. 01, 0. 02, 0. 08, 0. 32, 1. 45, 6. 2, 22. 6, 62. 2, 119. 0
	0. 0, 0. 97, 1. 23, 1. 32, 1. 36, 1. 37, 1. 36, 1. 34, 1. 28, 1. 130. 64, -0. 64, -1. 13, -1. 28, -1. 34, -1. 37, -1. 36, -1. 32, -1. 23, -0. 9, -0. 2
	-0. 0001, -1. 47, -2. 8, -3. 9, -4. 65, -4. 98, -4. 87, -4. 33, -3. 4, -2. 16, -0. 74, 0. 74, 2. 17, 3. 14, 4. 33, 4. 87, 4. 98, 4. 65, 3. 9, 2. 8, 1. 4
	1. 0, 5. 8, 29. 3, 108. 9, 266. 4, 396. 7, 347. 1, 180. 5, 59. 2, 13. 5, 2. 4, 0. 4, 0. 07, 0. 01, 0. 005, 0. 003, 0. 002, 0. 004, 0. 009, 0. 03, 0. 1
	403. 4, 309. 0, 142. 2, 42. 1, 8. 9, 1. 56, 0. 26, 0. 05, 0. 01, 0. 0044, 0. 0026, 0. 0026, 0. 0044, 0. 01, 0. 05, 0. 263, 1. 56, 8. 95, 42. 1, 142. 2, 309. 9
	0. 78, 1. 22, 1. 34, 1. 39, 1. 42, 1. 43, 1. 42, 1. 41, 1. 37, 1. 3, 1. 1, 0. 1, -1. 1, -1. 2, -1. 33, -1. 36, -1. 37, -1. 35, -1. 3, 1. 17, -0. 65
	1. 0, -0. 77, -2. 3, -3. 6, -4. 6, -4. 9, -4. 8, -4. 1, -3. 1, -1. 6, 0. 1, 1. 9, 3. 6, 5. 1, 6. 2, 6. 84, 6. 98, 6. 58, 5. 69, 4. 4, 2. 7
	1. 0, 7. 8, 51. 5, 238. 1, 675. 9, 1075. 4, 620. 1, 429. 3, 110. 8, 20. 8, 2. 83, 0. 35, 0. 04, 0. 01, 0. 002, 0. 001, 0. 001, 0. 001, 0. 004, 0. 02, 0. 12
	1. 10, 1. 32, 1. 40, 1. 43, 1. 45, 1. 46, 1. 46, 1. 44, 1. 42, 1. 37, 1. 25, 0. 76, -0. 8, -1. 22, -1. 33, -1. 36, -1. 37, -1. 35, -1. 29, -1. 1, -0. 1
	2. 0, -0. 06, -1. 9, -3. 4, -4. 9, -4. 8, 4. 0, -2. 7, -1. 1, 0. 95, 3. 0, 5. 0, 6. 7, 8. 1, 8. 8, 8. 9, 8. 5, 7. 47, 5. 94, 4. 06

 

Лабораторная работа 16

ПОИСК ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИЙ ФУНКЦИЙ МЕТОДОМ ЗОЛОТОГО СЕЧЕНИЯ

 

Цель работы: научиться определять максимальные и минимальные значения функции на заданном интервале.

 

16. 1 Теоретические сведения

 

Поиск экстремумов функции одной переменной имеет не только самостоятельный интерес, а и является важным элементом процессов минимизации функций нескольких переменных (многомерного минимизации) при решении различных задач оптимизации.

Метод, который описывается ниже, позволяет найти точку экстремума функции f(x) на интервале [a, b]. Для уверенности поиска отрезок [a, b] должен содержать один максимум или минимум исследуемой функции.

Золотым сечением отрезка называют длинные его на две части таким образом, что отношение длины всего отрезка к длине большей части равна отношению длины большей части к меньшей.

Нетрудно доказать, что золотой сечение отрезка [a, b] выполняют две симметрично расположенные точки:

 

	(16. 1)
где	(16. 2)

 

Причем точка x₁ в свою очередь делает золотое сечение отрезка [a, x2], а точка x₂ - отрезка [x1, b].

 

16. 2 Задание

 

Найти максимальное или минимальное значение функции на интервале [a, b] с точностью . Исходные Данные приведены в таблице 16. 1. Построить график функции и определить на нем точку экстремума.

 

16. 3 Методические рекомендации

В соответствии с вышеизложенным, поиск минимального значения функции на заданном интервале [a, b] может быть выполнен следующим образом:

- Отрезок [a, b] делим точками x₁ и x₂ по правилу золотого сечения;

- Вычисляем значение функции, минимизируется, f(x) в точках x₁ и x₂;

- При f(x₁) > f(x₂) меняем левую границу интервала a=x₁, а в противном случае - правую b=x₂;

- Повторяем процесс сначала, учитывая, что одна из точек золотого сечения уже известна;

- Итерации продолжаем до тех пор, пока интервал неопределенности [a, b] не станет меньше заданной погрешности;

- После завершения итераций точку минимума можно уточнить, разделив отрезок [a, b] пополам:

 

 

Аналогично можно найти максимум функции. Блок-схема метода представлена на рис. 16. 1.

 

 

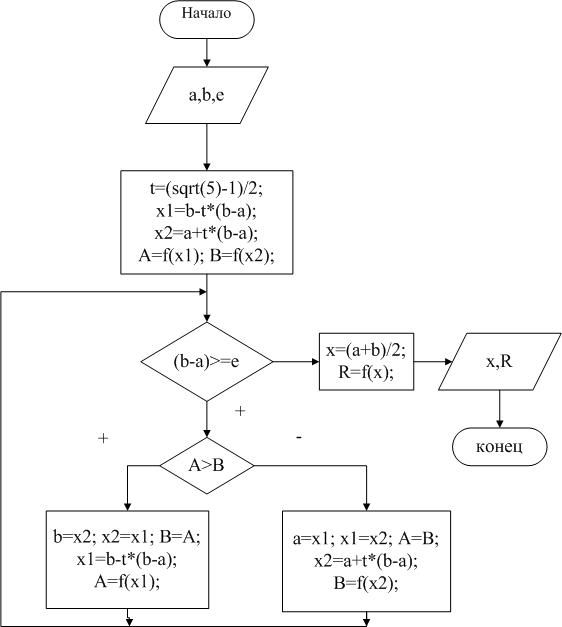
Рисунок 16. 1 - Алгоритм функции вычисления методом золотого сечения

 

Таблица 16. 1 – Задание к лабораторной работе №16

№ п/п	f(x)	a	b		Вид экстремума
				10-5	min
				10-4	max
		-1		10-3	min
				10-5	max
		-2		10-4	min
				10-3	max
		-2		10-4	min
				10-5	max
		-2		10-3	min
		-1		10-3	max
				10-3	min
				12 -6	max
				10-4	min
				10-5	max
		-1		10-4	min
		0, 1		10-3	max
		0, 1	0, 18	10-6	min
		-0, 1	0, 6	10-5	max
		-1		10-4	min
		-1		10-3	max
		1, 6		10-4	min
		0, 2	0, 5	10-6	max
		-5		10-3	min
		0, 5	1, 6	10-4	max
		0, 1		10-5	min

 

ЛИТЕРАТУРА

 

1. Маликов В. Т., Кветный Р. Н. Вычислительные методы и применение ЭВМ. – К.: Вища школа, 1999. - 212 с.

2. Мудров А. Е. Численные методы для ПЭВМ на языках Бейсик, Фортран, Паскаль. - Томск, 1991. - 272 с.

3. Боглаев Ю. П. Вычислительная математика и программирование. – М.: Высшая школа. 1990. - 544 с.

4. Копченова Н. В., Марон И. А. Вычислительная математика в примерах и задачах. – М.: Высшая школа. 1972. - 366 с.

5. Калиткин Н. Н. Численные методы. – М.: Наука, 1978. - 512 с.

 

Содержание

 

Введение
Лабораторная работа №1	Вычисление значений степенного полинома по схеме Горнера……………….
Лабораторная работа №2	Простейшие операции над матрицами……
Лабораторная робота №3	Решение систем линейных уравнений с действительными коэффициентами
Лабораторная работа №4	Решение систем линейных уравнений с комплексными коэффициентами………….
Лабораторная работа №5	Обращение матриц…………………………
Лабораторная работа №6	Вычисление определителей матриц………
Лабораторная работа №7	Отделение корней трансцендентных уравнений………………………….. ……….
Лабораторная работа №8	Отделение корней алгебраических уравнений………………………………….
Лабораторная работа №9	Уточнение корней трансцендентных и алгебраических уравнений………………...
Лабораторная робота №10	Разрешения систем нелинейных уравнений…………………………………...
Лабораторная робота №11	Численное решение линейных дифференциальных уравнений……………
Лабораторная робота №12	Интерполяция………………………………
Лабораторная робота №13	Аппроксимация методом наименьших квадратов……………………………………
Лабораторная робота №14	Численное интегрирование……………….
Лабораторная робота №15	Гармонический анализ и синтез периодических функций………………….
Лабораторная робота №16	Поиск экстремальных значений функций методом золотого сечения………………..

 

 

Методические указания к лабораторным работам по курсу “Математические методы и модели” (для студентов специальности 7. 090603)

 

Составили:      Джура Сергей Георгиевич, к. т. н., доцент

                       Шлепнев Сергей Владимирович, к. т. н., доцент

                       Якимишина Виктория Викторовна, к. т. н., доцент

Фёдоров Анатолий Юрьевич, ассистент

 

⇐ Предыдущая3456789101112

Поделиться:

Воспользуйтесь поиском по сайту: