 |
Линейные кинематические характеристики
|
|
|
|
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
Механика – это наука о машинах, механических движениях материальных тел и происходящих при этом взаимодействиях между ними, об искусстве построения машин.
Механическое движение – это изменение с течением времени взаимного положения тел в пространстве.
Классическая механика, в основе которой лежат законы Ньютона, изучает движение материальных тел, обладающих скоростями значительно меньшими скорости света. Движение тел со скоростями, близкими скорости света, рассматривает релятивистская механика, другое ее название –специальная теорииотносительности. Скорость распространения света принято обозначать латинской буквой с, в вакууме скорость света с ≈ 3·108 м/с. Рассмотрением движения элементарных частиц занимается квантовая механика.
Для описания движения материальных тел вводятся абстрактные понятия, отражающие те или иные реальные свойства тел:
1. Материальная точка – это имеющий массу объект, размерами которого в условиях данной задачи можно пренебречь.
2. Абсолютно твердое тело – это тело, у которого при его движении расстояние между любыми точками остается постоянным.
3. Абсолютно упругое тело – это тело, которое после прекращения на него внешнего механического воздействия, полностью восстанавливает свою первоначальную форму и размеры.
4. Абсолютно неупругое тело – это тело, которое после прекращения на него внешнего воздействия остается в деформированном состоянии.
5. Пространство и время. Все тела существуют и движутся в пространстве и во времени. Пространство выражает порядок сосуществования объектов, время – порядок смены явлений.
5. Система отсчета в механике – это совокупность тел отсчета, системы координат, связанной с телами отсчета, и часов, связанных с телом, по отношению к которому изучается движение материальных точек или тел. В классической механике свойства пространства описываются геометрией Евклида, а ход времени одинаков во всех системах отсчета.
|
|
|
Элементы кинематики
Сведения о векторах
Векторными называются величины, характеризующиеся не только численным значением (модулем), но и направлением. На чертежах векторы изображаются в виде прямолинейных отрезков со стрелкой на конце. Длина отрезка определяет модуль вектора, стрелка – его направление. В тексте векторы обозначают буквами жирного шрифта или над буквой ставится стрелка.
Сложение векторов осуществляется по следующей схеме: начало каждого последующего вектора совмещают с концом предыдущего, результирующий вектор проводится из начала первого в конец последнего. Эта операция называется правилом многоугольника.
Умножение векторов может производиться на скалярную или векторную величину. Умножение векторов друг на друга может быть векторное или скалярное.
Векторным произведением векторов a и b называется вектор c, определяемый формулой
c = a х b = [ a b ] = | a |·| b |· sin α · n,
где | a |и | b | – модули перемножаемых векторов, α – угол между перемножаемыми векторами, n – единичный вектор (его модуль равен единице), направленный перпендикулярно к плоскости, в которой лежат векторы-сомножители. Направление вектора n, а стало быть, и результирующего вектора с, находят по правилу правой руки. Захватив четырьмя сгибаемыми в кулак пальцами сначала умножаемый вектор, а затем тот, на который умножают, по отогнутому большому пальцу определяют направление результирующего вектора. На чертежах векторы, направленные к нам, обозначают точкой (•), а от нас –крестиком (+).
Скалярное произведение векторов a и b вычисляется по формуле
|
|
|
с = a · b = (a b) = | a |·| b | cos α.
Радиус-вектором r некоторой точки А называется вектор, проведенный из выбранного начала координат в данную точку (рис.1). Его проекции на координатные оси равны декартовым координатам данной точки x, y, z. Умножив их на единичные векторы i, j, k, вектор r можно представить в виде
r = x · i + y · j + z · k,
а его модуль
 .
.
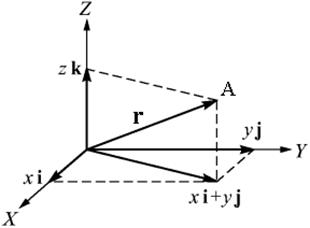
Рис. 1. Разложение радиус-вектора на составляющие вдоль координатных осей
Линейные кинематические характеристики
Материальная точка при своем движении описывает некоторую пространственную кривую, называемую траекторией, иллюстрация движения материальной точки приведена на рис.2. В зависимости от формы траектории различают прямолинейное или криволинейное движение.

Рис. 2. Траектория и перемещение материальной точки
В момент времени t 1 координаты точки могут быть определены радиус-вектором r 1, в момент времени t 2 – радиус-вектором r 2. Пройденное точкой за время t 2 – t 1 расстояние, отсчитанное вдоль траектории, называется путь (Δ S). Прямолинейный отрезок Δ r, соединяющий начальное и конечное положение материальной точки, называют вектором перемещения, он равен
Δ r = r 2 – r 1 = Δ X· i + Δ Y · j + Δ Z · k.
Заметим, что величина Δ S, строго говоря, не равна модулю |Δ r |. Только, когда Δ S → 0, Δ r по модулю приближается к Δ S.
Средняя скорость точки равна
V ср = Δ S /(t 2 – t 1) = Δ S /Δ t.
Скоростью точки в момент времени t называется вектор V, равный первой производной по времени от радиус-вектора
V = lim Δ r / Δ t = d r / dt.
Δ t →0
Вектор скорости направлен по касательной к траектории в сторону ее движения. Модуль скорости равен первой производной по времени от пути этой точки
V = lim Δ S /Δ t = dS / dt.
Δ t →0
Вектор скорости можно представить через его проекции на координатные оси
V = V x · i + V y· j + V z· k
или через производные по времени от проекций вектора r на оси координат
V = d r / dt = ( dx / dt)· i +( dy / dt)· j + ( dz / dt)· k.
Следовательно,
V x = dx / dt, V y = dy / dt, V z = dz / dt,
а модуль вектора скорости
V = (V x2+ V y2+ V z2)1/2.
При неравномерном движении скорость изменяется во времени. Изменение скорости в единицу времени называется ускорением. Мгновенное ускорение, то есть ускорение в данной точке, равно первой производной по времени от скорости:
|
|
|
a = d V / dt = (dV x/ dt)· i + (dV y/ dt)· j +(dV z/ dt)· k = а x i + а y j + а z k,
а модуль ускорения
а = (а x2+ а y2+ а z2)1/2.
При криволинейном движении материальной точки вектор ускорения удобно разложить на две составляющие. Одна из них а t – тангенциальное ускорение, направленное по касательной к траектории движения, а другая a n – нормальное или центростремительное ускорение, направленное перпендикулярно к a t. Тангенциальное ускорение характеризует изменение скорости по величине, нормальное – по направлению. Модуль полного ускорения можно найти как
a = (a n2 + a t2)1/2.
При этом модуль тангенциального ускорения равен a t = V 2/ R, где V –скорость, R – радиус кривизны траектории в окрестности данной точки. Криволинейную траекторию любой формы можно представить себе как совокупность элементарных участков, каждый из которых рассматривается как дуга окружности некоторого радиуса R.
Равнопеременное движение – это движение с постоянным ускорением. Для равнопеременного поступательного движения, если начало отсчета координаты тела начинается от положения, в котором оно находилось в момент начала отсчета времени, справедливы следующие соотношения между модулями перемещения, скорости и ускорения:
a = const; V t = V o + at; S = V 0 t + at 2/2; V t2 – V o2 = 2 aS.
Индексы " о" относятся к началу отсчета, а индексы " t " – к моменту времени t. В системе СИ размерности времени, перемещения, скорости и ускорения соответственно – секунда (с), метр (м), м/с, м/с2.
|
|
|


