 |
I. Взаимное положение прямых в пространстве, конкурирующие точки.
|
|
|
|
Билет №1.
I. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ, КОНКУРИРУЮЩИЕ ТОЧКИ.
1. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ.
Взаимное положение прямых в пространстве: параллельные прямые, пересекающиеся и скрещивающиеся.
Параллельные прямые
Параллельные прямые - это прямые, лежащие в одной плоскости и никогда не пересекающиеся, сколько бы их не продлевали.
Параллельные прямые имеют параллельные одноименные проекции. Обычно по двум проекциям пары прямых можно сделать заключение о их параллельности, однако если эти две прямые параллельны профильной плоскости проекций, то без рассмотрения третьей проекции прямых ничего утверждать нельзя.
Пересекающиеся прямые.
Параллельные прямые - это прямые лежащие в одной плоскости и имеющие одну точку пересечения.
Линии пересекающиеся в пространстве проектируются в виде пересекающихся проекций, причем проекции точки пересечения будут лежать на одной линии связи перпендикулярной оси Х.
Скрещивающиеся прямые
Скрещивающиеся прямые - это прямые не параллельные и не пресекающиеся между собой. Эти прямые не имеют общей точки и не лежат в одной плоскости.
2. Конкурирующие точки.
Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими.
На( рис. а ) приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости π 1 (А1 = В1). Такие точки называются горизонтально конкурирующими.
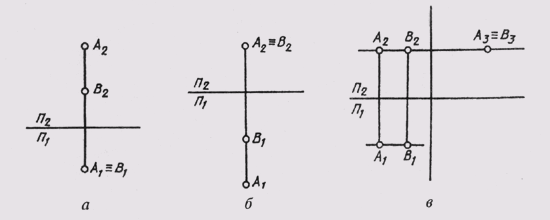
Если проекции точек A и В совпадают на плоскости Π 2 (рис. б ), они называются фронтально конкурирующими.
|
|
|
И если проекции точек А и В совпадают на плоскости π 3 (А3 = B3) (рис. в ), они называются профильно конкурирующими.
По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующихточек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.
II. ОСНОВЫ СПОСОБА ВРАЩЕНИЯ.
При вращении вокруг некоторой неподвижной прямой (ось вращения) каждая точка вращаемой фигуры перемещается в плоскости, перпендикулярной к оси вращения (плоскость вращения). Точка перемещается по окружности, центр которой находится в точке пересечения оси с плоскостью вращения (центр вращения), а радиус окружности равняется расстоянию от вращаемой точки до центра (это радиус вращения). Если какая-либо из точек данной системы находится на оси вращения, то при вращении системы эта точка считается неподвижной.
Ось вращения может быть задана или выбрана; в последнем случае выгодно расположить ось перпендикулярно к одной из плоскостей проекций, так как при этом упрощаются построения.
ВРАЩЕНИЕ ТОЧКИ, ОТРЕЗКА ПРЯМОЙ, ПЛОСКОСТИ ВОКРУГ ОСИ, ПЕРПЕНДИКУЛЯРНОЙ К ПЛОСКОСТИ ПРОЕКЦИЙ.
Вращение вокруг заданной оси.
Рис 212 Рис 213 Рис 214
1. Чертеж дан на рис. 212 справа: окружность, описанная точкой А при вращении ее вокруг оси, спроецирована без искажения на пл. П1 Из точки О', как из центра, проведена окружность радиуса R = О'А'; на пл. П 2 эта окружность изображена отрезком прямой, равным 2R.
На рис. 213 изображено вращение точки А вокруг оси, перпендикулярной к пл. П2. Окружность, описанная точкой А, спроецирована без искажения на пл. П2. Из точки 0", как из центра, проведена окружность радиуса R= О'А'; на пл. П1 эта окружность изображена отрезком прямой, равным 2R.
|
|
|
Из рассмотрения рис. 212 и рис. 231 отчетливо видно, что при вращении точки вокруг оси, перпендикулярной к какой-нибудь из плоскостей проекций, одна из проекций вращаемой точки перемещается по прямой, перпендикулярной к проекции оси вращения.
1. 
Теперь рассмотрим поворот отрезка прямой линии вокруг заданной оси.
Рис. 215 Рис. 216
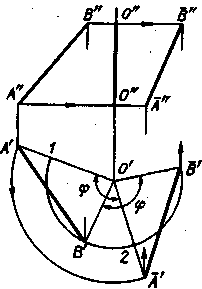
Так как в треугольниках А' В'О' и А' В'О' (рис. 215) стороны В'О' и А'О' треугольника А'В'О' равны (как радиусы) соответственно сторонам В'О' и А'О' треугольника А' В'О' и углы, заключенные между указанными сторонами, также равны, то эти треугольники равны между собой. Значит, А'В1 = А' В', величина горизонтальной проекции отрезка, повернутого вокруг оси, перпендикулярной к пл. П1 не изменяется. Очевидно, такое же заключение справедливо в отношении фронтальной проекции отрезка при его повороте вокруг оси, перпендикулярной к пл. П2.
В равных между собой треугольниках А'В'О' и А' В'О' (рис. _215) будут равны и их высоты, проведенные, например, из точки О' на А'В' и А' В'.
Указанным способом можно не только повернуть отрезок на заданный угол, но и определить угол, на который надо повернуть заданный отрезок, чтобы придать ему некоторое требуемое положение (например, расположить параллельно плоскости П2).
3. Поворот плоскости вокруг заданной оси сводится к повороту принадлежащих ей точек и прямых линий.
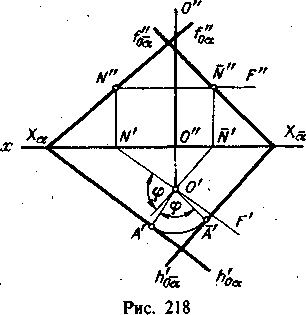
Рис. 217
Это соответствует тому, что угол наклона пл. ABC по отношению к пл. П1 не изменяется, ; если ось вращения перпендикулярна к пл. П1. Очевидно, при повороте вокруг оси, перпендикулярной к пл. П2, не изменяется угол наклона вращаемой плоскости к пл. П2 и сохраняется величина фронтальных проекций. При вращении, плоскости, выраженной ее следами, обычно поворачивают один из следов и горизонталь (или фронталь) плоскости. Пример дан на рис. 218.
|
|
|
