 |
Вращение вокруг выбранной оси.
|
|
|
|
Вращение вокруг выбранной оси.
В ряде случаев ось вращения может быть выбрана. При этом, если ось вращения выбрать проходящей через один из концов отрезка, то построение упростится, так как точка, через которую проходит ось, будет " неподвижной" и для поворота отрезка надо построить новое положение проекций только одной точки -- другого конца. Именно такое положение показано на рис. 219.
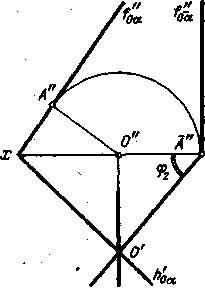
Рис. 219 рис. 221
Если при повороте плоскости, выраженной следами, можно выбрать ось вращения, то ее целесообразно расположить в плоскости проекций; построения в этом случае упрощаются. Пример дан на рис. 220. По сравнению с рис. 218 упрощение состоит в том, что отпала горизонталь. Она понадобилась бы в случае " ухода" точки Х за пределы чертежа; но в аналогичном случае на рис. 218 пришлось бы взять две вспомогательные линии. На рис. 221 плоскость общего положения повернута в положение горизонтально-проецирующей; при этом определился угол наклона пл. а к пл. П2. Если взять ось вращения, перпендикулярную к пл. П1 то можно пл. а поставить в положение фронтально-проецирующей, определив при этом угол наклона плоскости к пл. П1.
Билет № 3.
I. ПОСТРОЕНИЕ НА ЧЕРТЕЖЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ П1 и П2
Из рассмотрения левой части рис. 69 можно заключить, что отрезок АВ является гипотенузой прямоугольного треугольника АВ1, в котором один катет равен проекции отрезка (А1 = А°В°), а другой катет равен разности расстояний концов отрезка от плоскости проекций П0.
|
|
|
Если координаты, определяющие расстояния концов отрезка от плоскости проекций, имеют разные знаки (рис. 69, справа), то надо иметь в виду разность алгебраическую:
В1 = ВВ° - (-АА0) = ВВ° + АА°.
Угол прямой линии с плоскостью проекций определяется как угол, составленный прямой с ее проекцией на этой плоскости. Этот _ угол входит в тот же прямоугольный треугольник, который строят для определения натуральной величины отрезка. Очевидно, зная по чертежу катеты треугольника, можно его построить в любом месте поля чертежа. На рис. 70 показано построение, примененное Г. Монжем:
Рис. 70 рис. 71 рис. 72
На рис. 71 слева длина отрезка АВ и угол, составленный прямой АВ с пл. П1 определены из прямоугольного треугольника, построенного на проекции А'В' при втором катете В'В*, равном В" 1. АВ = А'В*.
На рис. 71 справа длина отрезка и угол, составленный с пл. п2, определены из прямоугольного треугольника, построенного на проекции А" В" (А" А* = А'2). АВ = В" А*.
Действительно (рис. 72), в прямоугольном треугольнике N”M”M’ сумма углов φ + φ 2 = 90°. Но в треугольниках N”M”M’ и N”N’M’ при общей гипотенузе N” M’ катет N" M” больше катета N”N’ и следовательно, φ > φ 1. Подставляя в φ + φ 2=90° угол φ 1 вместо φ, получим φ 1+ φ 2< 90°.
рис. 75 рис. 76 
На рис. 75 дан пример определения расстояния от точки А до точки О. Сначала построены проекции искомого отрезка - А" О" и А'О' (точка О выражена ее проекциями О" и О'). Затем построен треугольник А'О'А*, один катет которого - проекция А'О', другой - отрезок А'А* = А" АХ. Искомое расстояние определяется гипотенузой О'А*.
Теперь мы можем определить угол, составляемый прямой, равнонаклоненной к плоскостям П1, П2 и П3, с этими плоскостями. Об этом угле говорилось в и была указана его величина ( ≈ 35°). Ее можно определить, если рассмотреть хотя бы рис. 76: проекции А" В" и А'В' равны между собой, и углы А" В" 1 и 2А'В' равны каждый 45°.
|
|
|
II. 
СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ СФЕР И ЕГО ПРИМЕНЕНИЕ ПРИ ПОСТРОЕНИИ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ.
|
|
|
