 |
Раздел 1. Определители и матрицы. Решение систем линейных уравнений
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
По дисциплине «Элементы высшей математики»
для студентов заочной формы обучения
Для специальности 230115 «Программирование в компьютерных системах»
2014 г.
| СОГЛАСОВАНО Цикловой комиссией физико-математических и общих естественнонаучных дисциплин Председатель ______________ Е.О. Кузнецова | УТВЕРЖДАЮ Начальник учебного отдела _______________ Е.Н. Круглова «___» ________________ 2014 г. |
«___» _______________ 2014 г.
Разработали преподаватели Е.О.Кузнецова и Н.В.Сельцина
ОГЛАВЛЕНИЕ
Пояснительная записка
РАЗДЕЛ 1. ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Основные понятия и определения
Вычисление определителей 2-го порядка.
Миноры и алгебраические дополнения элементов определителя
Вычисление определителей 3-го порядка
Матрицы. Основные понятия и определения
Виды матриц
Элементарные преобразования матриц
Системы n линейных уравнений с n неизвестными. Основные понятия и определения
Метод Крамера решения систем линейных уравнений
Метод Гаусса решения систем линейных уравнений
РАЗДЕЛ 2 ПРЕДЕЛ ФУНКЦИИ.
Определение предела функции
Основные теоремы о пределах функции
Вычисление пределов функций
2.3.1 Раскрытие неопределенности типа 
2.3.2 Раскрытие неопределенности типа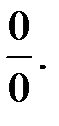 
2.3.3 Раскрытие неопределенности типа 
.
РАЗДЕЛ 3. ПРОИЗВОДНАЯ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ И СЛОЖНЫХ ФУНКЦИЙ.
Задача, приводящая к понятию производной. Определение производной.
Определение производной функции
|
|
|
Основные правила дифференцирования
Таблица производных элементарных функций
Таблица производных сложных функций
Приложение производной к вычислению пределов функций.
Правило Лопиталя.
РАЗДЕЛ 4 ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ.
Интервалы монотонности функции
Экстремумы функции
Интервалы выпуклости и вогнутости графика функции. Точки перегиба.
Асимптоты графика функции
Общая схема исследования функции и построение её графика
РАЗДЕЛ 5. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
5.1. Неопределённый интеграл: основные понятия, определения, свойства
Основные свойства неопределённого интеграла
Таблица простейших интегралов
Основные методы интегрирования
Непосредственное интегрирование
Метод замены переменной (способ подстановки).
Интегрирование по частям
РАЗДЕЛ 6. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
6.1. Определённый интеграл: основные понятия, определения, свойства.
Свойства определённого интеграла
Формула Ньютона - Лейбница. Основные методы вычисления определённого интеграла.
Непосредственное интегрирование
Геометрические приложения определенного интеграла.
Вычисление площади плоской фигуры.
РАЗДЕЛ 7. КОМПЛЕКСНЫЕ ЧИСЛА.
Понятие комплексного числа, алгебраическая форма записи комплексного числа. Действия с комплексными числами в алгебраической форме.
Действия с комплексными числами в алгебраической форме записи.
Геометрическое изображение комплексного числа
Тригонометрическая и показательная формы записи комплексного числа. Действия с комплексными числами в этих формах
Решение задач
РАЗДЕЛ 8. РЯДЫ
Ряды. Основные определения. Признаки сходимости рядов
|
|
|
Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
ЛИТЕРАТУРА
ПРИЛОЖЕНИЯ
Приложение 1
Приложение 2
Приложение 3
Приложение 4
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Методические указания для учебной дисциплины «Элементы высшей математики» разработаны на основе Федерального государственного образовательного стандарта по специальности среднего профессионального образования 230115 «Программирование в компьютерных системах»
В структуре основной профессиональной образовательной программы учебная дисциплина «Элементы высшей математики» входит в математический и общий естественнонаучный цикл.
В методических указаниях рассмотрены все темы дисциплины, необходимые для выполнения контрольной работы, приведены теоретические материалы, примеры решения заданий и задания для самостоятельной работы студентов по каждой теме с целью закрепления и углубления теоретических знаний и приобретения необходимых умений и навыков, а также для самоконтроля.
В результате изучения обязательной части цикла студент должен
уметь:
- выполнять операции над матрицами и решать системы линейных уравнений;
- решать задачи, используя уравнения прямых и кривых второго порядка на плоскости;
- применять методы дифференциального и интегрального исчисления; -решать дифференциальные уравнения; - пользоваться понятиями теории комплексных чисел.
знать:
- основы математического анализа, линейной алгебры и аналитической геометрии;
- основы дифференциального и интегрального исчисления;
- основы теории комплексных чисел.
Курс высшей математики является базовым инструментом практически всех технических дисциплин и поэтому обучение владению математическими методами является обязательным условием при подготовке любого высококлассного специалиста технического профиля.
РАЗДЕЛ 1. ОПРЕДЕЛИТЕЛИ И МАТРИЦЫ. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Основные понятия и определения
Определителем называется число, заданное квадратной таблицей вида
, где 
- числа, называемые элементами определителя,
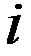- номер строки, 
- номер столбца определителя на пересечении которых стоит элемент определителя 
.
|
|
|
, 
- обозначения определителя.
Количество строк (или столбцов) определителя называют порядком определителя.
Так, определитель
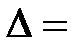
является определителем 2-го порядка,
определитель
является определителем 3-го порядка,
определитель
имеет 
-ый порядок.
|
|
|
