 |
Вычисление определителей 2-го порядка.
|
|
|
|
Рассмотрим определитель второго порядка:
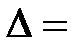

Элементы 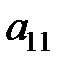 и
и 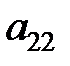 определителя 2-го порядка образуют его главную диагональ, элементы
определителя 2-го порядка образуют его главную диагональ, элементы 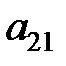 и
и 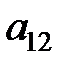 образуют побочную диагональ определителя.
образуют побочную диагональ определителя.
Правило вычисления определителя второго порядка:
определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали, т.е.
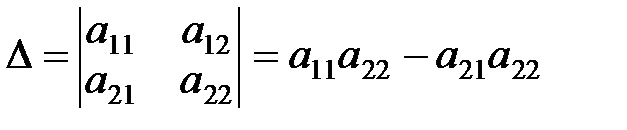 .
.
Пример 1. Вычислить определитель 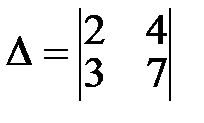 .
.
Решение. По правилу вычисления определителя 2-го порядка имеем:
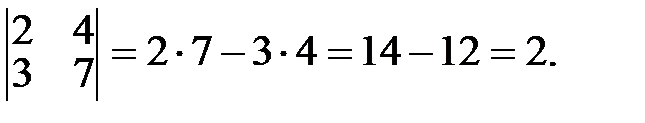
Пример 2. Вычислить определитель 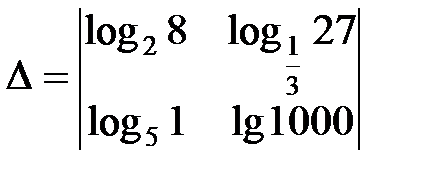 .
.
Решение. Заменим логарифмы, являющиеся элементами определителя, их значениями:
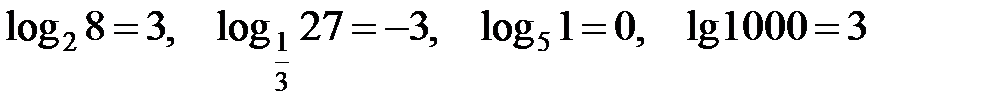 ,
,
тогда получим
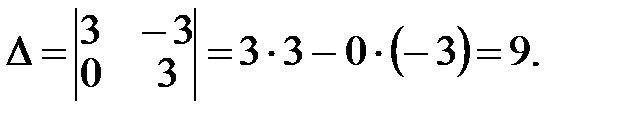
Упражнения
№1. Вычислить определители 2-го порядка:
1. 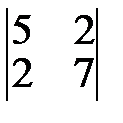 2.
2. 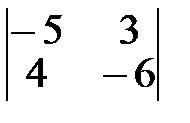
3. 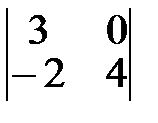 4.
4. 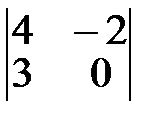
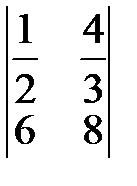
5. 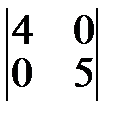 6.
6. 
Миноры и алгебраические дополнения элементов определителя.
Минором 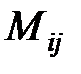 элемента
элемента 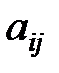 определителя
определителя 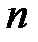 -го порядка называется определитель
-го порядка называется определитель 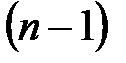 -го порядка, получаемый из исходного определителя вычеркиванием
-го порядка, получаемый из исходного определителя вычеркиванием 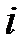 -ой строки и
-ой строки и  -го столбца.
-го столбца.
Пример 1. Найти миноры всех элементов определителя 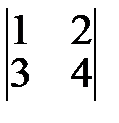 .
.
Решение. 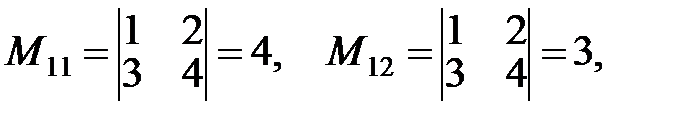

Пример 2. Найти миноры элементов 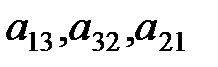 определителя
определителя 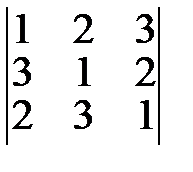 .
.
Решение.
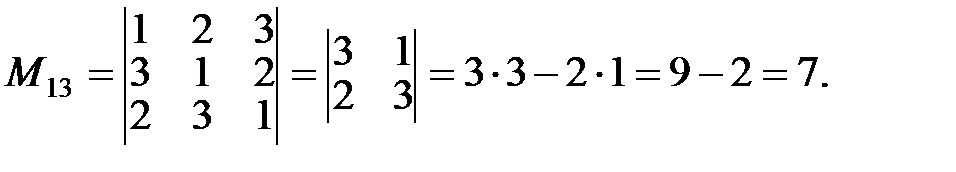
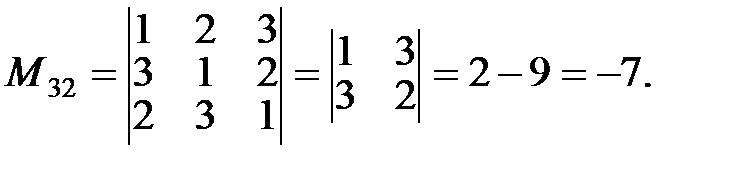
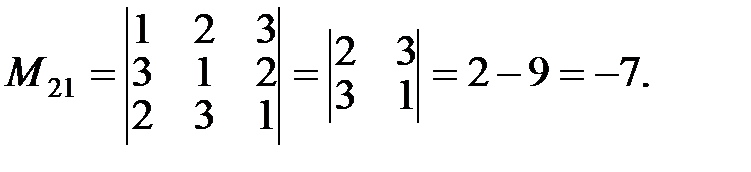
Алгебраическим дополнением 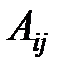 элемента
элемента 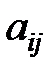 определителя
определителя 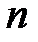 -го порядка называется его минор, взятый со знаком
-го порядка называется его минор, взятый со знаком 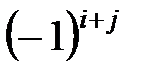 , т.е.
, т.е.
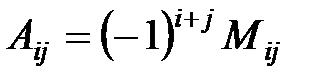 .
.
Из формулы видно, что перед алгебраическим дополнением 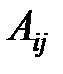 берётся знак +, если сумма индексов
берётся знак +, если сумма индексов 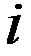 и
и 
 чётная, и знак -, если эта сумма нечётная.
чётная, и знак -, если эта сумма нечётная.
Пример. Найти алгебраические дополнения элементов 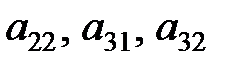 определителя 3-го порядка
определителя 3-го порядка 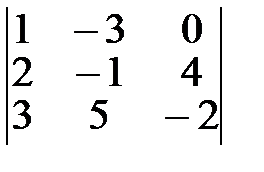 .
.
Решение.
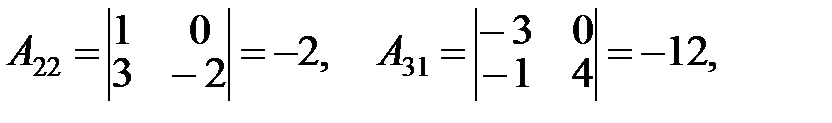
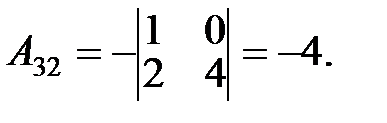
Упражнения.
Найти алгебраические дополнения всех элементов определителя:
1. 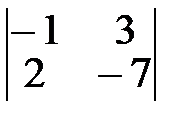 2.
2. 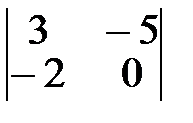
3. 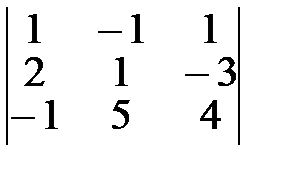 4.
4. 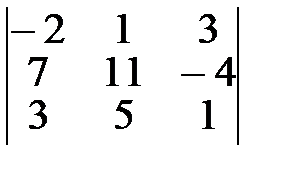
Вычисление определителей 3-го порядка.
Определитель 3-го порядка вычисляют двумя способами: по правилу треугольников и разложением определителя по элементам какой-либо строки (столбца)
|
|
|
1.4.1 Правило треугольников.
В этом случае значение определителя вычисляют как сумму шести слагаемых, каждое из которых представляет собой произведение трёх элементов определителя, выбираемых по следующему правилу: три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников берутся со знаком +,
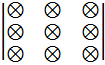
а три произведения элементов, стоящих на побочной диагонали и в вершинах двух других треугольников берутся со знаком --, т.е. вычисление определителя выполняется по следующей схеме:

т.е. вычисление определителя выполняется по следующей схеме:
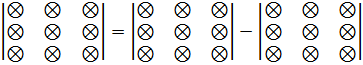
Пример. Вычислить определитель 3-го порядка 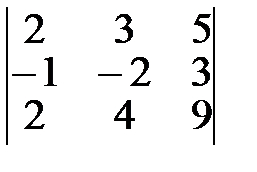 .
.
Решение.
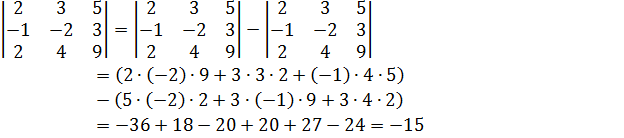
Упражнения
Вычислить определители третьего порядка по правилу треугольников:
1. 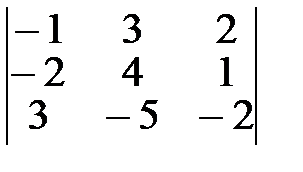 2.
2. 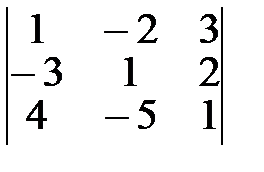
3. 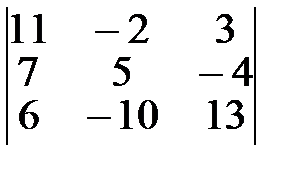 4.
4. 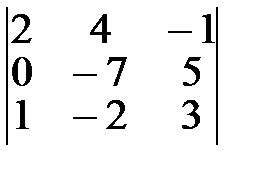
Замечание:
с помощью правила треугольников можно вычислять только определители третьего порядка.
1.4.2 Разложение определителя по элементам какой-либо строки
(столбца).
В данном случае значение определителя находят как сумму произведений элементов какой-либо строки (столбца) определителя на их алгебраические дополнения:
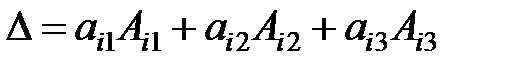 - разложение по элементам
- разложение по элементам 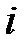 -ой строки;
-ой строки; 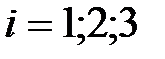 .
.
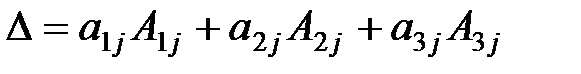 - разложение по элементам
- разложение по элементам  -ого столбца;
-ого столбца; 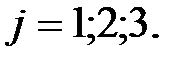
Пример. Вычислить определитель 3-го порядка 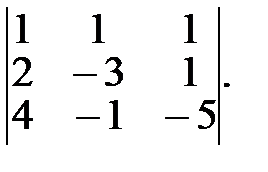
Решение. Вычислим данный определитель разложением по элементам первой строки:
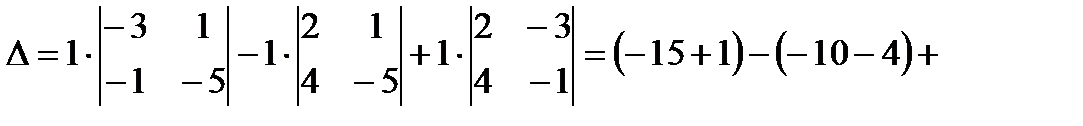
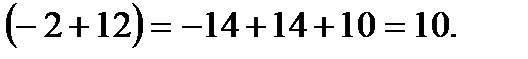
Замечание:
разложением по элементам какой-либо строки (столбца) вычисляют и определители высших (4-го, 5-го и т.д.) порядков, что утверждает теорема Лапласа:
определитель любого порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
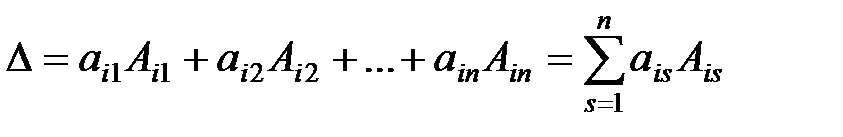 -разложение по элементам
-разложение по элементам 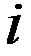 -ой строки;
-ой строки; 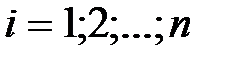
 -разложение по элементам
-разложение по элементам  - го столбца;
- го столбца; 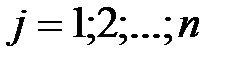 .
.
Пример. Вычислить определитель 4-го порядка 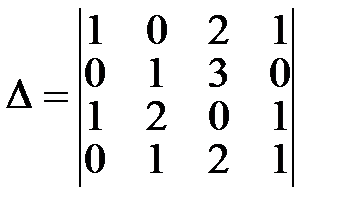 .
.
Решение. Данный определитель лучше раскладывать по элементам 1-го столбца, т.к. два элемента в нём являются нулями:
|
|
|
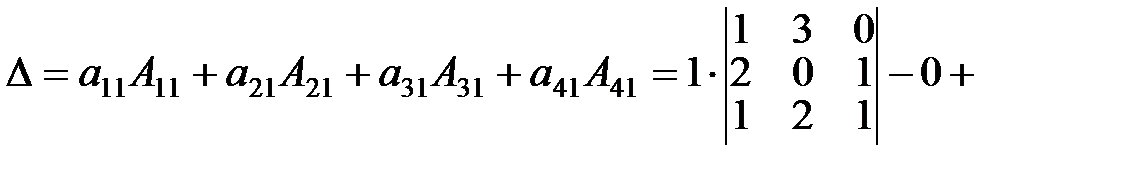
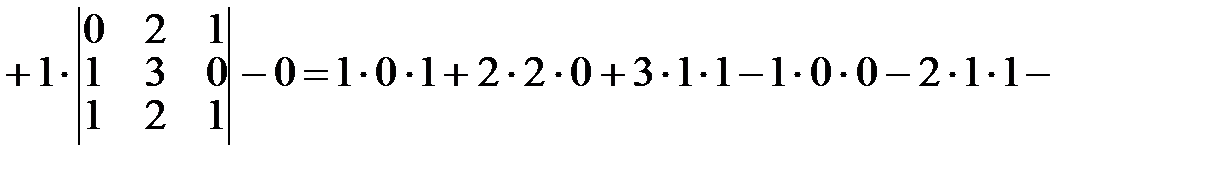
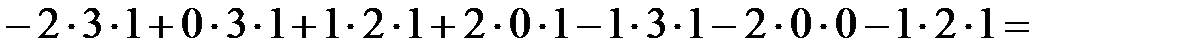
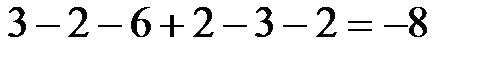 .
.
Упражнения.
№1. Вычислить определитель третьего порядка разложением по элементам 1-ой строки: 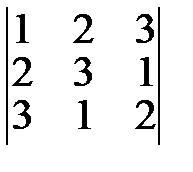
№2. Вычислить определитель третьего порядка разложением по элементам 3-го столбца:
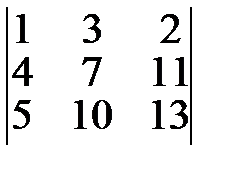
Матрицы. Основные понятия и определения
Матрицей размером 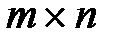 называется прямоугольная таблица чисел, содержащая
называется прямоугольная таблица чисел, содержащая 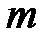 строк и
строк и 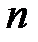 столбцов.
столбцов.
Числа, из которых состоит матрица, называются элементами матрицы.
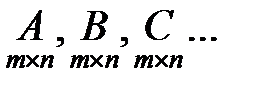 - обозначения матриц размером
- обозначения матриц размером 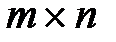 ,
,
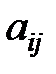 - обозначение элементов матрицы, где
- обозначение элементов матрицы, где 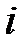 - номер строки,
- номер строки,  - номер столбца.
- номер столбца.
Например,
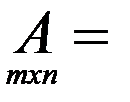
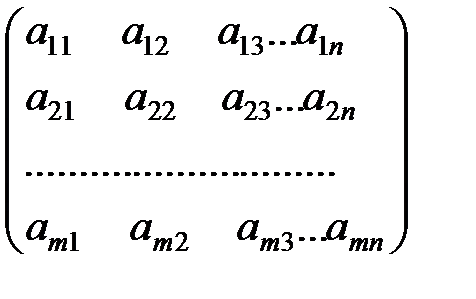 - матрица размером
- матрица размером 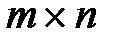 .
.
Две матрицы называются равными, если они одного размера и поэлементно совпадают, т.е.
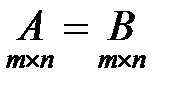 , если
, если  для любых
для любых 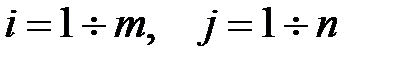 .
.
Виды матриц.
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой.
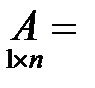
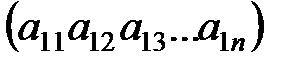 - вектор-строка.
- вектор-строка.
Матрица, состоящая из одного столбца, называется матрицей (вектором)- столбцом.
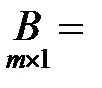
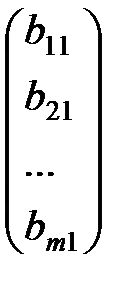 - вектор-столбец.
- вектор-столбец.
Матрица, состоящая из 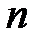 строк и
строк и 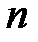 столбцов называется квадратной матрицей
столбцов называется квадратной матрицей 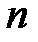 -го порядка.
-го порядка.
Например, матрица
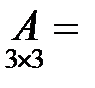
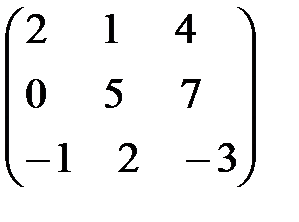 является квадратной матрицей третьего порядка.
является квадратной матрицей третьего порядка.
Элементы матрицы, у которых номер строки и номер столбца совпадают, называются диагональными и образуют главную диагональ матрицы.
Для квадратной матрицы главную диагональ образуют элементы 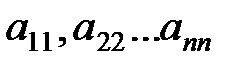 .
.
Если все недиагональные элементы квадратной матрицы равны 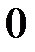 , то матрица называется диагональной.
, то матрица называется диагональной.
Например, матрица
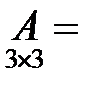
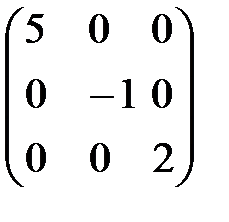 является диагональной матрицей третьего порядка.
является диагональной матрицей третьего порядка.
Если у диагональной матрицы 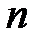 -го порядка
-го порядка  все диагональные элементы равны
все диагональные элементы равны 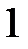 , то матрица называется единичной матрицей
, то матрица называется единичной матрицей 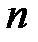 -го порядка и обозначается буквой
-го порядка и обозначается буквой 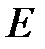 .
.
Например,
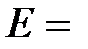
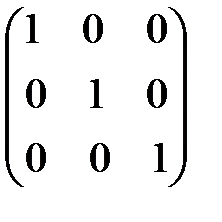 - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Матрица любого размера называется нулевой, или нуль-матрицей, если все её элементы равны 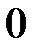 .
.
Например,
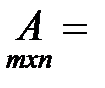
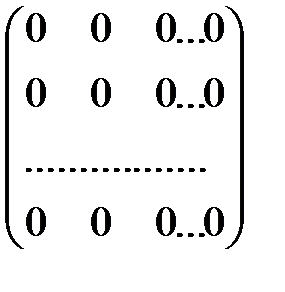 - нуль-матрица размером
- нуль-матрица размером 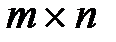 .
.
|
|
|


