 |
Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
|
|
|
|
Необходимый признак сходимости ряда: Ряд 
может сходиться лишь в том случае, если его общий член 
стремится к 0 при n 
=0
Достаточный признак расходимости ряда. Если же общий член не стремится к 0 => ряд расходится
0
Предостережение: необходимое условие =0 недостаточно для сходимости ряда. Ряд у которого 
, может сходиться, а может и расходиться.
Пример 1. Ряд 0,4 +0,44+0,444+0,4444+…
расходится, т.к. общий член 
не стремится к 0.
Пример 2. Ряд 1-1+1-1+…
расходится т.к. общий член = 
не стремится к 0.
И вообще не имеет предела.
Пример 3. Ряд 
расходится, т.к. 
Пример 4. Ряд 
расходится, т.к. 
.
Но:
5) Ряд 
+…+ 
называется гармоническим рядом и является расходящимся рядом, т.к. последовательность его частичных сумм неограниченно возрастает.
Т.е. необходимый признак сходимости не дает возможности судить о том, сходится ли данный ряд или нет. Сходимость и расходимость ряда во многих случаях можно установить с помощью достаточных признаков сходимости.
Рассмотрим некоторые из них для знакоположительных рядов, т.е. для рядов с неотрицательными членами (знакоотрицательный ряд переходит в знакоположительный путём умножения его на (-1), что не влияет на сходимость ряда).
Достаточные признаки сходимости
Признак сравнения рядов
Сходимость или расходимость знакоположительного ряда часто устанавливается путём сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет.
Часто «эталонными» рядами являются:
а) гармонический ряд 
– расходящийся или
б) геометрическая прогрессия: 
, 
· Если 
ряд сходится 
· Если 
ряд расходится
· Если 
ряд расходится
Пример: ряд 
Можно расписать так:
=> Это ряд геометрической прогрессии, где a= 
|
|
|
q= 
=> этот ряд сходится.
Теорема: Пусть даны два знакоположительных ряда
Если для всех n выполняется неравенство 
=> из сходимости второго ряда следует сходимость первого ряда, из расходимости ряда первого следует расходимость ряда второго.
Примеры:
1)Исследовать на сходимость ряд
Сравним данный ряд с рядом
–ряд геометрической прогрессии, который является сходящимся, т.к. q= 
Т.к. 
=> данный ряд сходится.
2)Исследовать на сходимость ряд:
Сравним данный ряд с гармоническим рядом:
1+ 
–ряд расходящийся
Т.к. каждый 
=> данный ряд расходится
3)Исследовать на сходимость ряд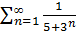 
Сравним с рядом геометрической прогрессии:
, который сходится (q= 
Т.к. 
=> данный ряд сходится
4)Сходимость ряда: 1+ 
Сравнить с рядом геометрической прогрессии
1+ 
– сходится.
Признак Даламбера
Теорема: Пусть дан знакоположительный ряд 
+… и существует конечный или бесконечный предел
Тогда ряд сходится при 
<1; и расходится при >1
(При 
= 1 вопрос о сходимости остаётся нерешённым)
(Признак Даламбера целесообразно применить, когда общий член ряда содержит n! или 
)
Примеры:
1)Исследовать на сходимость ряд
Находим 
= 
=> L=0<1 =>данный ряд по признаку Даламбера сходится.
2)Сходимость: 
L=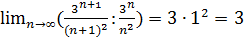 
L=3>1=> ряд по признаку Даламбера расходится.
Признак Коши (радикальный):
Пусть дан ряд 
и 
.
Если q>1, то ряд расходится.
Если q<1, то ряд сходится.
Признак Лейбница (для знакочередующегося ряда):
Пусть дан ряд 
Ряд сходится, если выполняются два условия:
1) элементы ряда по абсолютной величине монотонно убывают;
2) предел общего члена ряда равен нулю.
Степенным рядом называется ряд вида
или 
Чтобы найти интервал сходимости степенного ряда надо:
1) применить признак Даламбера или Коши к ряду, составленному из модулей;
2) исследовать сходимость ряда на концах интервала.
|
|
|
Решение задач
Пример 1.Исследовать на сходимость ряд 
Решение.
Т. к.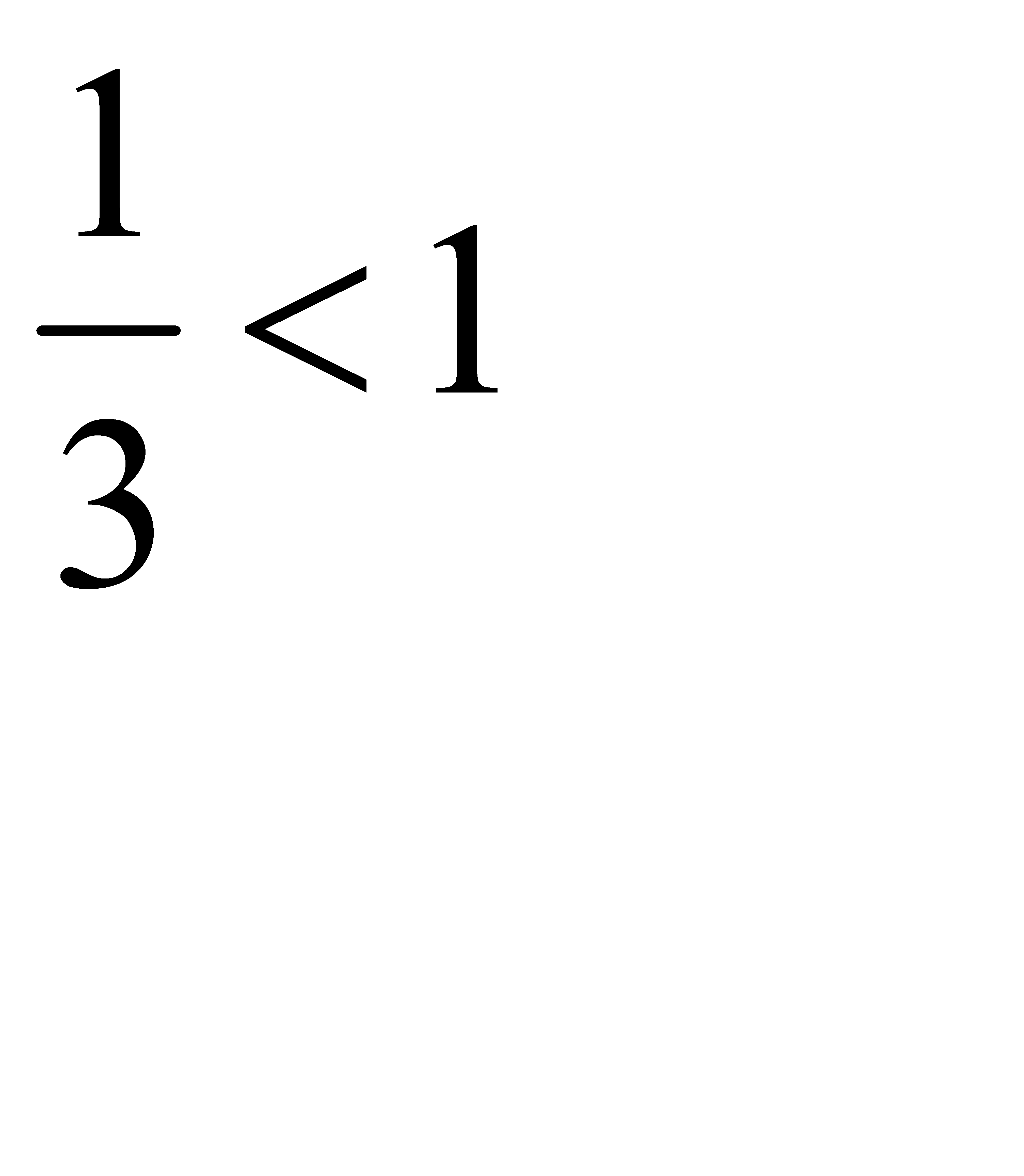 
, то ряд сходится по признаку Даламбера.
Пример2. Исследовать на сходимость ряд 
Решение.
Т. к. 
, то ряд расходится по признаку Даламбера.
Пример 3. Исследовать на сходимость ряд
Решение
Т.к. 
, то ряд расходится по признаку Коши.
Пример 4. Пользуясь признаком Лейбница, исследовать на сходимость ряд 
Решение.
Так как члены данного ряда по абсолютной величине монотонно
убывают 
и общий член ряда стремится к нулю 
, то в силу признака Лейбница ряд сходится.
Пример 5.Исследовать на абсолютную и условную сходимость ряды:
Решение.
а) Рассмотрим ряд, составленный из абсолютных величин
По признаку Даламбера этот ряд сходится, т.к.
Таким образом ряд расходится абсолютно.
б)Ряд, составленный из абсолютных величин членов данного ряда
- расходится как общегармонический (т.к. 
).
Следовательно, исходный ряд не является абсолютно сходящимся.
Исследуем его на условную сходимость.
Ряд сходится (по признаку Лейбница), так как
Итак, данный ряд сходится условно.
Пример 6. Найти область сходимости степенного ряда
Решение.
Рассмотрим ряд, составленный из абсолютных величин
По признаку Даламбера
Рассмотрим неравенство 
, откуда 
Исследуем сходимость ряда на концах промежутка.
При x=-3 получим ряд:
- этот ряд расходится как гармонический.
При x=-3 получим ряд:
- этот ряд сходится по признаку Лейбница.
Итак, интервалом сходимости данного ряда является промежуток
или 
Упражнения
Исследовать на сходимость ряды:
1) 
+ 
+ 
+ … + 
+ …
2) 
+ 
+ 
+ … + 
+ …
3) 
+ 
+ 
+ … + 
+ …
4) 
… + 
+ …
5) 
… + 
+ …
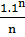6) 
+ 
+ 
+ … + 
+ …
7) 
+ 
+ 
+ … + 
+ …
8) 
|
|
|
