 |
Метод замены переменной (способ подстановки).
|
|
|
|
Найти заданный неопределённый интеграл непосредственным интегрированием удаётся далеко не всегда, а иногда это сопряжено с большими трудностями. В таких случаях применяют другие способы интегрирования.
Одним из наиболее эффективных методов является способ подстановки или замены переменной интегрирования.
Сущность этого метода заключается в том, что путём введения новой переменной интегрирования удаётся свести заданный интеграл к новому интегралу, который сравнительно лёгко берётся непосредственно.
Алгоритм метода:
Пусть дан интеграл  , который не является табличным.
, который не является табличным.
1. Записываем уравнение замены
 ,
,
где 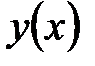 - некоторая функция.
- некоторая функция.
2. Находим дифференциал этой функции
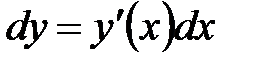 .
.
3. Выражаем
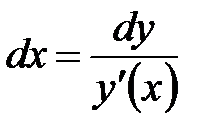 .
.
4. Подставим  и
и 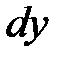 в данный интеграл:
в данный интеграл:
 .
.
Если замена выполнена правильно, то
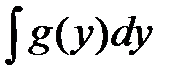
будет табличным.
5. Находим
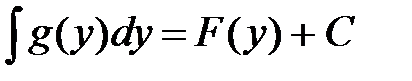 .
.
6. Чтобы получить окончательный ответ, вместо переменной  подставляем выражение
подставляем выражение  :
:
 .
.
Пример 1. Найти 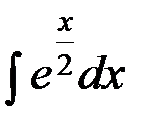 .
.
Решение. Сделаем подстановку 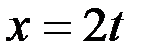 , тогда
, тогда  . Следовательно,
. Следовательно,

 .
.
Пример 2. Найти  .
.
Решение. Сделаем подстановку 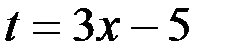 , тогда
, тогда  , следовательно,
, следовательно,
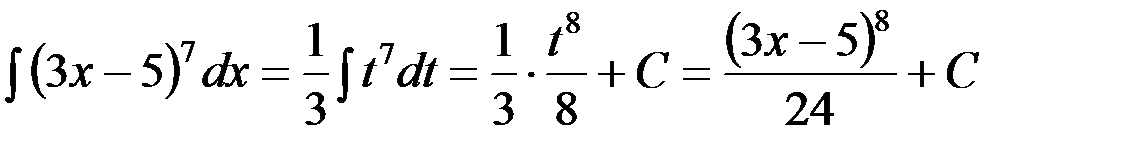 .
.
Пример 3. Найти 
Решение. Сделаем подстановку 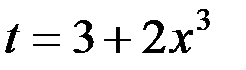 , тогда
, тогда  , следовательно,
, следовательно,
 .
.
Пример 4. Найти  .
.
Решение. Сделаем подстановку 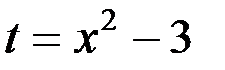 , тогда
, тогда 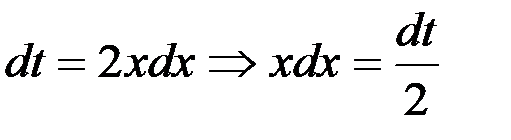 , получаем
, получаем
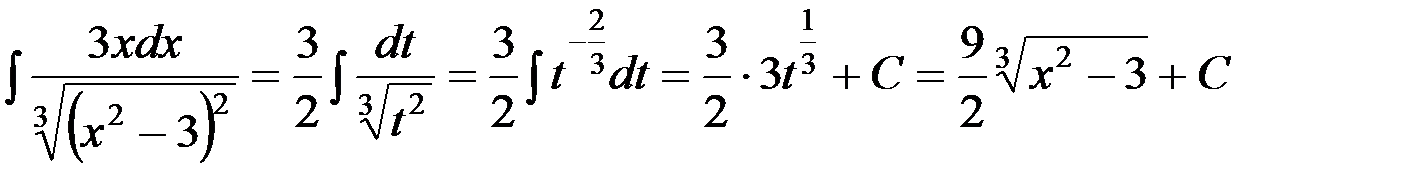 .
.
Пример 5. Найти 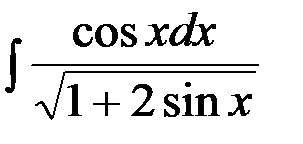 .
.
Решение. Подстановка  , тогда
, тогда  , получим
, получим
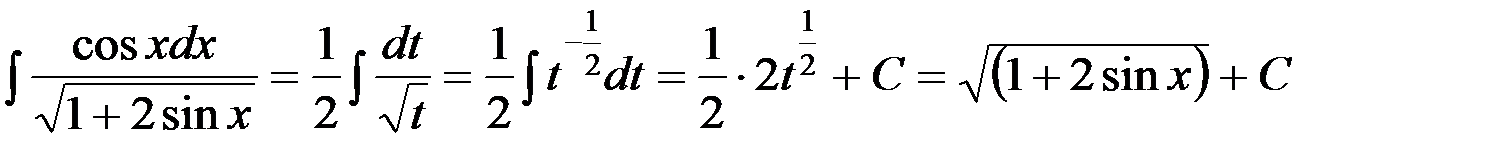 .
.
Пример 6. Найти 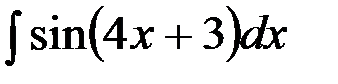 .
.
Решение. Сделаем подстановку  , тогда
, тогда  , следовательно,
, следовательно,
 .
.
Пример 7. Найти 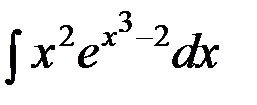 .
.
Решение. Сделаем подстановку  , тогда
, тогда  , следовательно,
, следовательно,
 .
.
Пример 8. Найти  .
.
Решение. Сделаем подстановку  , тогда
, тогда  , получим
, получим

Пример 9. Найти  .
.
Решение. Преобразуем подынтегральную функцию 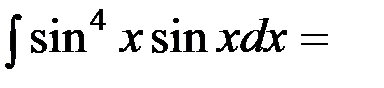
= 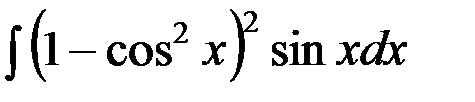 . Сделаем замену
. Сделаем замену 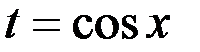 , тогда
, тогда 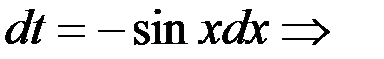
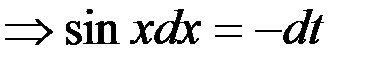 , получим
, получим
 =
=  .
.
Пример 10. Найти  .
.
Решение. Замена 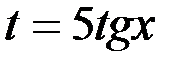 , тогда
, тогда  , получаем
, получаем
 .
.
|
|
|
Пример 11. Найти  .
.
Решение. Сделаем замену 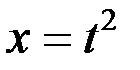 , тогда
, тогда 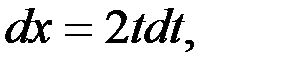 получаем
получаем
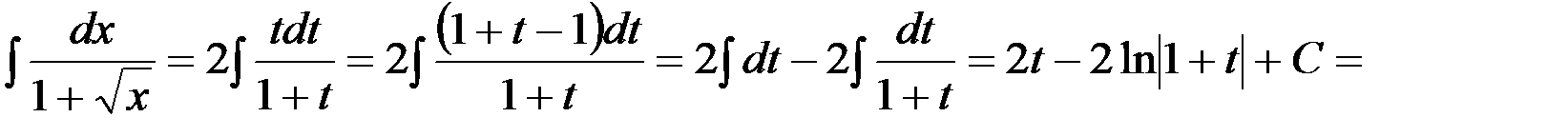
 .
.
Часто при нахождении неопределённых интегралов используются следующая теорема:
 ,
,
на основании которой может быть составлена следующая таблица интегралов от сложных функций, промежуточным аргументом которых является линейная функция:
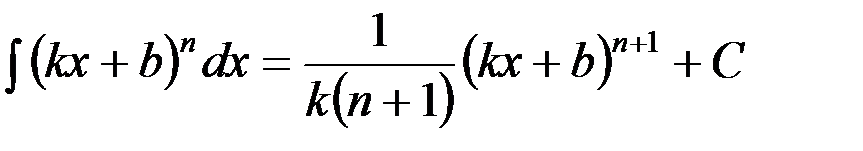
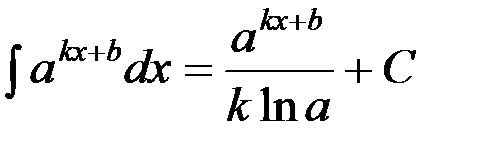
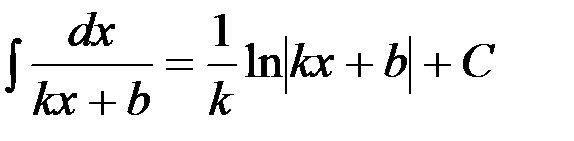







Пользуясь данной таблицей можно в некоторых случаях, не применяя метод замены переменной, сразу получать конечный результат.
Упражнения.
Найти неопределённые интегралы методом замены переменной
№1 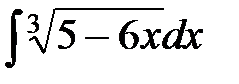 №2
№2 
№3  №4
№4 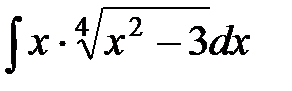
№5  №6
№6 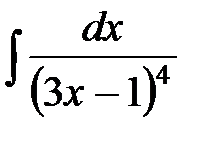
№7 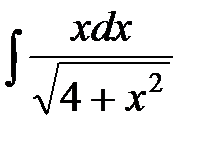 №8
№8 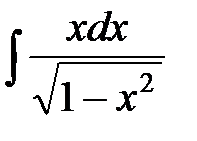
№9 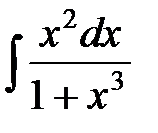 №10
№10 
№11.  №12.
№12. 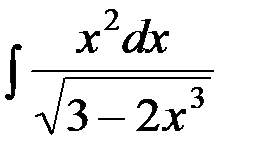
№13. 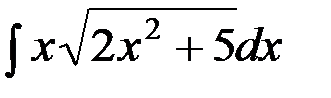 №14.
№14. 
№15. 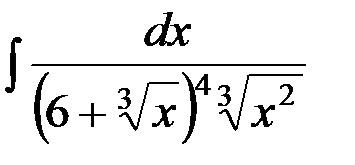 №16.
№16. 
№17. 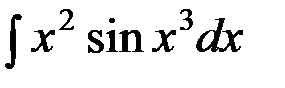 №18.
№18. 
№19. 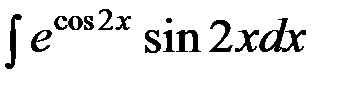 №20
№20 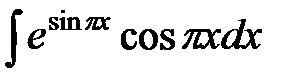
№21.  №22.
№22. 
№ 23.  №24.
№24. 
№25 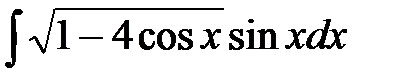 №26
№26 
№27.  №28.
№28. 
№29.  №30
№30 
№31. 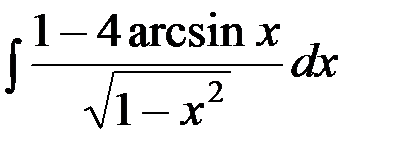 №32
№32 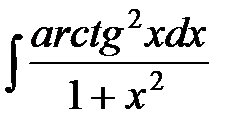
№33. 
 №34.
№34. 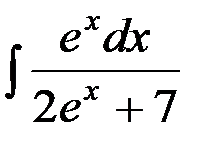
Интегрирование по частям.
Интегрирование по частям – это, практически, формула интегрирования произведения двух функций.
Хорошо известна формула дифференциала произведения двух функций:

Проинтегрировав обе части данного равенства, получим:
 ,
,
т.к.
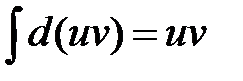 ,
,
то
 ,
,
откуда
 .
.
Последняя формула называется формулой интегрирования по частям.
Формула интегрирования по частям сводит нахождение интеграла  к отысканию другого интеграла
к отысканию другого интеграла  ; её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо подобен ему.
; её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо подобен ему.
При этом в качестве  берётся функция, которую проще продифференцировать, а в качестве
берётся функция, которую проще продифференцировать, а в качестве  берётся та часть подынтегрального выражения, которую проще проинтегрировать. Иногда формулу интегрирования по частям приходиться использовать несколько раз.
берётся та часть подынтегрального выражения, которую проще проинтегрировать. Иногда формулу интегрирования по частям приходиться использовать несколько раз.
При применении формулы интегрирования по частям интегралы можно разбить на 3 основные группы:
1. В интегралах вида
 ,
,
где 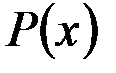 - многочлен переменной
- многочлен переменной 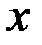 ,
, 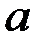 - число, полагают
- число, полагают

2. В интегралах вида

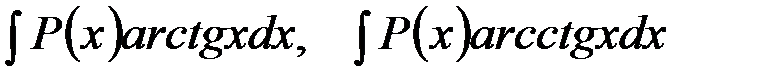
полагают

3. В интегралах вида

за  принимают любую функцию, за
принимают любую функцию, за  соответственно оставшуюся часть подынтегрального выражения.
соответственно оставшуюся часть подынтегрального выражения.
|
|
|
Пример 1. Найти  .
.
Решение. Данный интеграл относится к первой группе, поэтому

 .
.
Пример 2. Найти  .
.
Решение. Данный интеграл относится ко второй группе, поэтому положим 
Тогда по формуле интегрирования по частям находим:
 .
.
Пример 3. Найти  .
.
Данный интеграл относится к первой группе, поэтому 
 , по формуле интегрирования по частям имеем
, по формуле интегрирования по частям имеем
 .
.
Пример 4. Найти  .
.
Решение. Интеграл относится к первой группе, поэтому 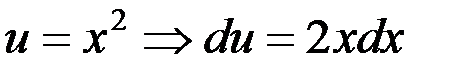 ,
,  , тогда имеем
, тогда имеем
 .
.
К последнему интегралу снова применим формулу интегрирования по частям, положив  , тогда получим
, тогда получим
 .
.
Исходный интеграл равен
 .
.
Пример5. Найти  .
.
Решение. Данный интеграл относится ко второй группе, поэтому  . По формуле интегрирования по частям получим
. По формуле интегрирования по частям получим

= 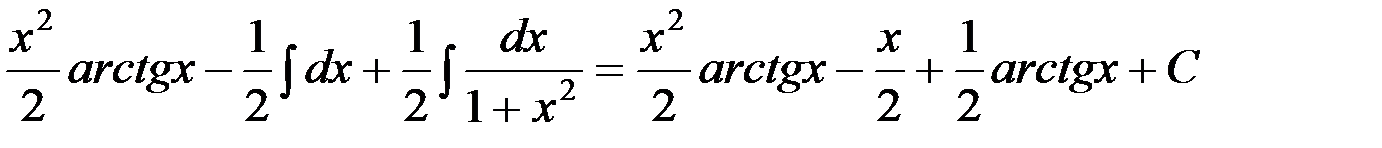 .
.
Пример 6. Найти  .
.
Решение. Данный интеграл относится к третьей группе, поэтому выбор  и
и  в данном случае произволен. Пусть
в данном случае произволен. Пусть  ,
,  , тогда по формуле интегрирования по частям получим
, тогда по формуле интегрирования по частям получим
 .
.
Для второго интеграла применим ещё раз формулу интегрирования по частям:
 ,
,
тогда
 .
.
Подставляя полученное выражение в соотношение для исходного интеграла, получим
 .
.
Перенесём интеграл из правой части в левую, получим

Упражнения
Найти неопределённый интеграл методом интегрирования по частям:
№1. 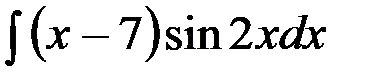 №2.
№2. 
№3. 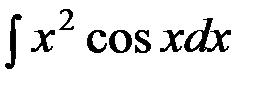 №4.
№4. 
№5.  №6.
№6. 
№7.  №8
№8 
№9.  №10.
№10. 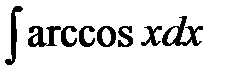
|
|
|


