 |
Метод Гаусса решения систем линейных уравнений.
|
|
|
|
Одним из способов решения систем линейных уравнений является метод Гаусса, который является универсальным способом решения систем линейных уравнений, т.к. во-первых, с помощью этого метода можно решать системы линейных уравнений любого порядка, во-вторых, этим методом можно решать не только квадратные, но и прямоугольные системы уравнений.
Суть метода Гаусса состоит в следующем:
1. Составляют расширенную матрицу системы (записывают матрицу коэффициентов, через вертикальную черту от неё записывают столбец свободных членов)
2. С помощью элементарных преобразований основную матрицу системы (матрицу коэффициентов) приводят к единичному виду. Тогда в столбце свободных членов получают решение системы.
Пример. Решить методом Гаусса систему уравнений: 
Решение. Составим расширенную матрицу системы:
.
Для того, чтобы привести основную матрицу к диагональному виду, будем обнулять все диагональные элементы с помощью элементарных преобразований.
Например, возьмём сначала в качестве ведущего элемента 
и обнулим элементы первого столбца из второй и третьей строки с помощью следующих элементарных преобразований: 
,
тогда получим:
.
Теперь в качестве ведущего элемента удобнее выбрать элемент 
и обнулить элементы второго столбца второй и первой строки с помощью следующих элементарных преобразований: 
,
после чего получим
.
Вторую строку последней матрицы можно разделить на -8, а третью строку на -1, тогда имеем
.
Теперь выбираем в качестве ведущего элемента 
и обнулим элементы третьего столбца первой и третьей строки с помощью следующих преобразований: 
,
тогда получим:
. 
Для того чтобы привести основную матрицу к единичному виду и получить окончательный ответ, переставим местами вторую и третью строку матрицы:
|
|
|
.
Ответ: 
.
Упражнения.
Решить системы уравнений методами Крамера и Гаусса:
1. 
2. 
3. 
4. 
РАЗДЕЛ 2 ПРЕДЕЛ ФУНКЦИИ.
Определение предела функции
Пусть функция 
определена во всех точках промежутка 
, за исключением, быть может, некоторой точки 
. Составим последовательность значений аргумента функции 
:
, таким образом, чтобы все члены последовательности принадлежали промежутку 
, и последовательность сходилась к точке 
, т.е.
.
Тогда значения функции 
также образуют числовую последовательность
Определение 1. Число 
является пределом функции 
при 
, стремящемся к 
, если для любой последовательности аргументов, сходящейся к числу 
, последовательность значений функции сходится к числу 
.
Обозначение предела функции при 
:
.
Определение 2. Число 
является пределом функции 
при 
, стремящемся к 
, если для любого положительного числа 
существует такое положительное число 
, зависящее от 
, что при всех 
, удовлетворяющих неравенству
выполняется неравенство
.
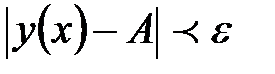Основные теоремы о пределах функции.
Пусть функции 
и 
имеют пределы при 
, стремящемся к 
, т.е.
,
тогда справедливы следующие теоремы:
1. Предел суммы (разности) двух (или более ) функций равен сумме (разности) пределов каждой из этих функций.
2. Предел произведения двух (или более) функций равен произведению пределов каждой из этих функций.
Следствие.
Постоянный множитель можно выносить за знак предела.
Предел частного двух функций равен частному пределов каждой из этих функций.
.
(в этом случае предполагается, что функция 
в достаточно малой окрестности точки 
и 
).
1. Если существует 
и 
-элементарная функция, то
|
|
|
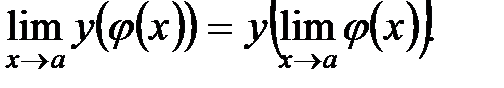
