 |
I специальный (замечательный) предел
|
|
|
|

Этот предел позволяет заменять функцию синус при достаточно малых значениях аргумента самим аргументом, т.е.  при
при  .
.
Для более общего случая I специальный (замечательный) предел имеет вид:

Пример 1.Вычислить 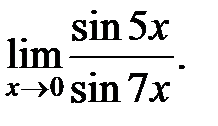
Решение. Т.к. при  , аргументы также стремятся к 0, то можно заменить тригонометрические функции, стоящие в предельном выражении, их аргументами:
, аргументы также стремятся к 0, то можно заменить тригонометрические функции, стоящие в предельном выражении, их аргументами:
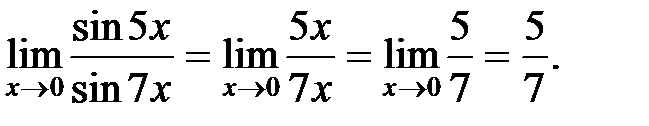
Пример 2.Вычислить 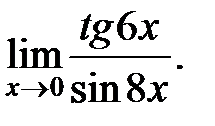
Решение. Выполним преобразование предельного выражения:

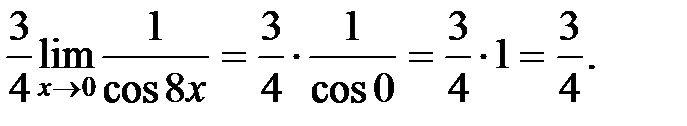
Пример 3. Вычислить 
Решение. Выполним в предельном выражении следующие преобразования

тогда
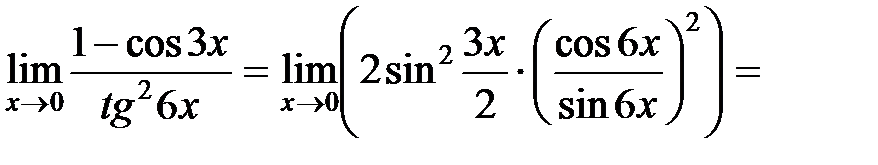
= 
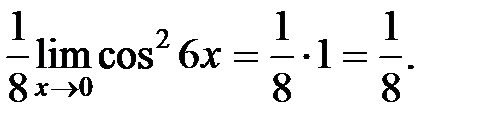
Пример 4.Вычислить 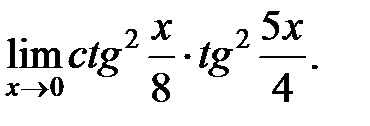
Решение. Применим в предельном выражении определение тригонометрических функций тангенс и котангенс, а затем I специальный предел:

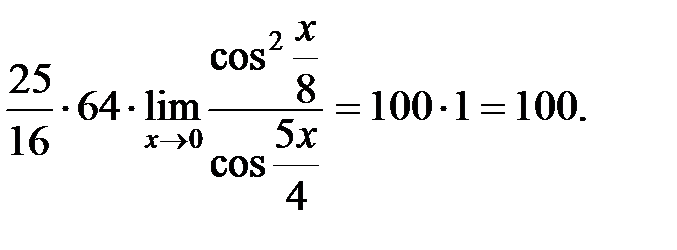
Пример 5. Вычислить 
Решение. Сделаем замену  тогда
тогда 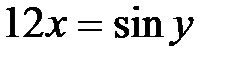 ,
,  .
.

Упражнения
Вычислить пределы:
1.  Ответ:
Ответ: 
2.  Ответ:
Ответ: 
3.  Ответ:
Ответ: 
4.  Ответ:
Ответ: 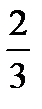
5. 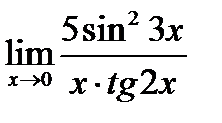 Ответ:
Ответ: 
6.  Ответ:
Ответ: 
7.  Ответ:
Ответ: 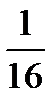
8.  Ответ:
Ответ: 
9.  Ответ:
Ответ: 
10. 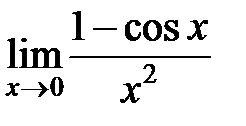 Ответ:
Ответ: 
11. 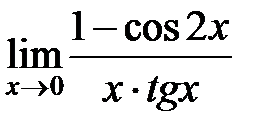 Ответ:
Ответ: 
12.  Ответ:
Ответ: 
2.3.3 Раскрытие неопределенности типа  .
.
При раскрытии неопределённости типа  применяют различные алгебраические преобразования предельного выражения, в результате чего получают неопределённости типа
применяют различные алгебраические преобразования предельного выражения, в результате чего получают неопределённости типа 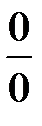 или
или  , которые раскрываются описанными выше способами.
, которые раскрываются описанными выше способами.
Пример 1. 
Решение. Умножим и разделим предельное выражение на  :
:

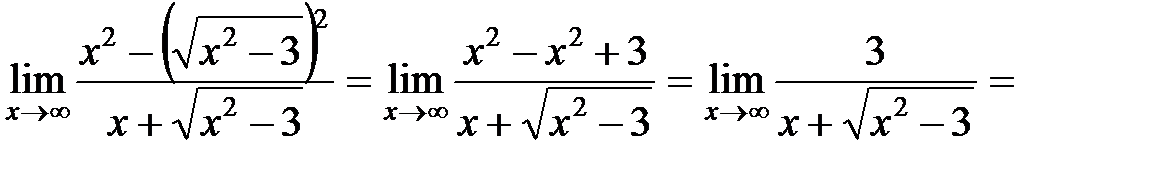
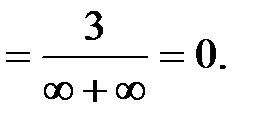
Пример 2. Вычислить 
Решение. Выполним в предельном выражении вычитание дробей, приведя их для этого к общему знаменателю:


Упражнения.
Вычислить пределы:
1.  Ответ:
Ответ: 
2.  Ответ:
Ответ: 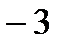
3.  Ответ:
Ответ: 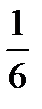
4. 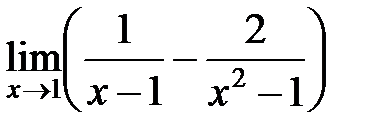
 Ответ:
Ответ: 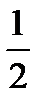
5.  Ответ: -1
Ответ: -1
6.  Ответ:
Ответ: 
7. 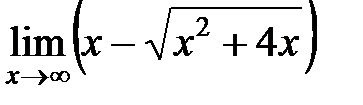 Ответ:
Ответ: 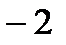
8.  Ответ:
Ответ: 
9. 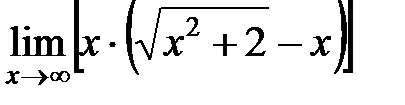 Ответ:
Ответ: 
10.  Ответ:
Ответ: 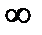
11.  Ответ:
Ответ: 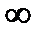
РАЗДЕЛ 3. ПРОИЗВОДНАЯ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ И СЛОЖНЫХ ФУНКЦИЙ.
|
|
|
Задача, приводящая к понятию производной. Определение производной.
Задача о мгновенной скорости.
Пусть материальная точка движется прямолинейно и неравномерно. Путь  , пройденный точкой, есть некоторая функция времени
, пройденный точкой, есть некоторая функция времени 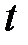 :
: 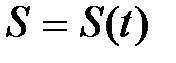 .
.
Требуется найти мгновенную скорость точки в некоторый момент времени  .
.
За время 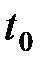 точка пройдёт путь
точка пройдёт путь  . За время
. За время 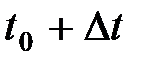 точка пройдёт путь
точка пройдёт путь 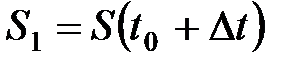 . Тогда за время
. Тогда за время  точка пройдёт путь
точка пройдёт путь 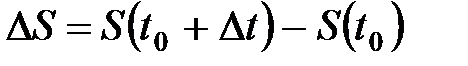 (рис. 1).
(рис. 1).
| S |
| S(t0) |
| S(t0 + Δt) |
| ΔS |
рис. 1
Тогда средняя скорость точки равна

 .
.
При 
 . Следовательно,
. Следовательно, 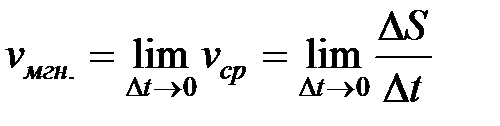 .
.
При решении многих практических задач требовалось вычисление предела вида  . Предел данного вида назвали производной функции
. Предел данного вида назвали производной функции  .
.
Определение производной функции.
Производной функции  называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  , когда приращение аргумента стремится к нулю.
, когда приращение аргумента стремится к нулю.
 - обозначение производной функции
- обозначение производной функции  .
.
Согласно определению  .
.
Функция, имеющая производную, называется дифференцируемой функцией.
Процесс нахождения производной функции называется дифференцированием функции.
Раздел математического анализа, занимающийся вопросами, связанными с производными функций одной переменной, называется дифференциальным исчислением функции одной переменной.
Основные правила дифференцирования.
Для нахождения производных различных функций удобнее применять не определение производной, а правила дифференцирования и таблицу производных функций.
Основные правила дифференцирования:
1. Производная постоянной величины.
Производная постоянной величины равна нулю.
 .
.
2. Производная суммы
Производная алгебраической суммы нескольких дифференцируемых функций равна алгебраической сумме производных каждой из них.
 .
.
Производная произведения.
Производная произведения двух дифференцируемых функций равна произведению первого сомножителя на производную второго плюс произведение второго сомножителя на производную первого, т.е.
|
|
|

Следствие.
Постоянный множитель можно выносить за знак производной, т.е.


4. Производная частного.
Если числитель и знаменатель дроби – дифференцируемые функции и знаменатель не обращается в нуль, то производная дроби равна также дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя, т.е.

|
|
|


