 |
Интервалы монотонности функции
|
|
|
|
Интервалом (промежутком) возрастания функции называется промежуток из области определения функции, на котором функция возрастает.
Интервалом (промежутком) убывания функции называется промежуток из области определения функции, на котором функция убывает.
Интервалы возрастания и убывания функции называются интервалами(промежутками) монотонности функции.
Интервалы монотонности функции можно определить с помощью первой производной.
Правило нахождения интервалов (промежутков) монотонности функции:
1. Найти область определения функции.
2. Найти производную  функции, а затем определить точки
функции, а затем определить точки  , в которых производная равна
, в которых производная равна  или
или  (критические точки), т.е. решить уравнения
(критические точки), т.е. решить уравнения  и
и  .
.
3. Область определения функции разбить критическими точками на числовые промежутки и определить знак 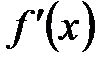 в каждом из полученных числовых промежутков.
в каждом из полученных числовых промежутков.
4. В тех промежутках, где  функция возрастает, в тех промежутках, где
функция возрастает, в тех промежутках, где  функция убывает.
функция убывает.
Пример 1. Найти интервалы монотонности функции 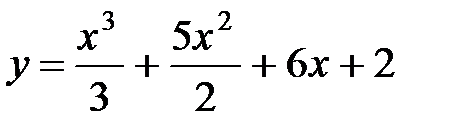 .
.
Решение. Т.к. функция является многочленом, то областью её определения является вся числовая ось. Найдём первую производную функции:
 .
.
Найдём критические точки функции, для чего решим уравнение
 .
.
 .
.
Разобьём область определения функции критическими точками на числовые промежутки и определим знак первой производной в каждом из полученных промежутков, результаты удобнее заносить в таблицу:
| 
| 
| 
|

| + | - | + |

| возрастает | убывает | возрастает |
Пример 2. Найти промежутки монотонности функции  .
.
Решение. Областью определения функции является вся числовая ось. Найдём первую производную функции, для удобства, представив второе слагаемое в виде степени:
|
|
|
 , тогда
, тогда

Найдём критические точки функции, для этого решим уравнения
 и
и  .
.


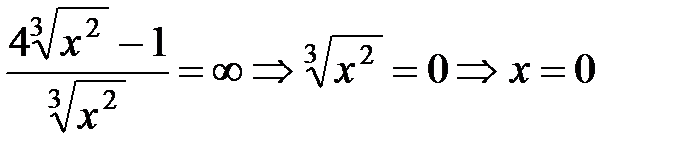 .
.
Получили 3 критические точки, которые разбивают область определения на 4 числовых промежутка, определим знаки первой производной в каждом из этих промежутков:

| 
| 
| 
| 
|

| + | - | + | - |

| возрастает | убывает | возрастает | убывает |
Упражнения.
Найти промежутки монотонности следующих функций:
1.  2.
2. 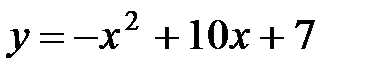
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11. 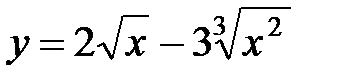 12.
12. 
Экстремумы функции
Точка  из области определения функции называется точкой максимума, если в некоторой окрестности этой точки выполняется условие
из области определения функции называется точкой максимума, если в некоторой окрестности этой точки выполняется условие
| у |
 .
.
| y(x0) |
| х0 |
| ( |
| ) |
| х |
Точка  из области определения функции называется точкой минимума, если в некоторой окрестности этой точки выполняется условие
из области определения функции называется точкой минимума, если в некоторой окрестности этой точки выполняется условие
 .
.
| y(x0) |
| х0 |
| ( |
| ) |
| х |
| у |
Точки максимума и минимума функции называются точками экстремума функции.
В точках экстремума промежуток возрастания сменяется на промежуток убывания (точка максимума), промежуток убывания сменяется на промежуток возрастания (точка минимума)
Значения функции в точках максимума и точках минимума называются максимумом и минимумом функции соответственно.
Максимум и минимум функции называются экстремумами функции.
Правило нахождения экстремумов функции с помощью первой производной:
1. Найти область определения функции.
2. Найти критические точки  функции
функции  , т.е. те точки из
, т.е. те точки из
области определения функции, в которых  или
или
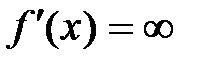 .
.
3. Найденными точками разбить область определения функции на
числовые промежутки.
4. Определить знак  в каждом из полученных числовых
в каждом из полученных числовых
промежутков.
5. Если при переходе через критическую точку  производная функции
производная функции
 меняет свой знак, то точка
меняет свой знак, то точка  является точкой экстремума
является точкой экстремума
функции; если знак  не меняется, то точка
не меняется, то точка  точкой экстремума
точкой экстремума
не является. При этом если при переходе через рассматриваемую точку
|
|
|
 слева направо знак
слева направо знак  меняется с минуса на плюс, то
меняется с минуса на плюс, то  -
-
точка минимума, если с плюса на минус, то  - точка максимума.
- точка максимума.
6. Для нахождения экстремумов функции вычислить значения функции
 в точках экстремума.
в точках экстремума.
Пример 1. Найти промежутки монотонности и экстремумы функции  .
.
Решение. Область определения функции  . Найдём производную функции
. Найдём производную функции
 .
.
Производная обращается в ноль при  Эти точки разбивают область определения функции на 4 числовых промежутка, в каждом из которых
Эти точки разбивают область определения функции на 4 числовых промежутка, в каждом из которых  сохраняет определённый знак. Найдём знаки производной в каждом из полученных промежутков:
сохраняет определённый знак. Найдём знаки производной в каждом из полученных промежутков:

| 
| - 
| 
| 
| 
|

|

|

| - | + | - | + | |||

| убывает | min | возрастает | max | убывает | min | возрастает |
Найдём значения функции в точках экстремума (экстремумы функции):
 .
.
Таким образом, максимумов функция достигает в точках  и
и  , минимума в точке
, минимума в точке  .
.
Пример 2. Найти точки экстремума и промежутки монотонности функции  .
.
Решение. Область определения данной функции  .
.
Найдём первую производную функции, воспользовавшись правилом дифференцирования производная произведения:
 =
=
 .
.
Найдём критические точки функции, приравняв первую производную к нулю и к бесконечности:
 ;
;
 .
.
Результаты исследования занесём в таблицу:

|

| -4 | 
| 
| 
|

| |
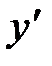
| + |

| + | - | + | ||
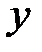
| возрастает | экстремума нет | возрастает |
max

| убывает | min | возрастает |
Упражнения
№1. Найти экстремумы заданных функций с помощью первой производной:
1. 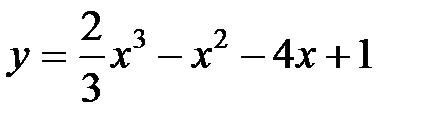 2.
2. 
3. 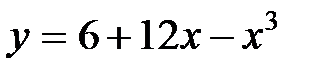 4.
4. 
5.  6.
6. 
7.  8.
8. 
№2. Найти интервалы монотонности и экстремумы функции:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 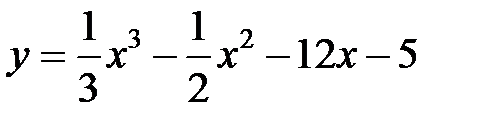
7.  8.
8. 
9.  10.
10. 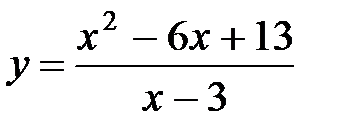
|
|
|


