 |
Вычисление площади плоской фигуры.
|
|
|
|
1) Как было показано выше, определённый интеграл от неотрицательной функции 
на отрезке 
численно равен площади криволинейной трапеции, ограниченной линиями 
(рис. 1).
Рис. 1.
Площадь заштрихованной фигуры вычисляется по формуле:
.
2) Если криволинейная трапеция ограничена линиями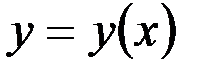 
, где 
, 
(рис. 2),
Рис. 2.
то площадь заштрихованной фигуры вычисляется по формуле:
.
3)Площадь фигуры, ограниченной линиями 
, где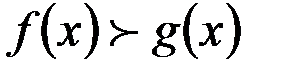 
и прямыми 
(рис. 3)
Рис. 3.
То площадь заштрихованной фигуры находят по формуле:
4) Если криволинейная трапеция ограничена линиями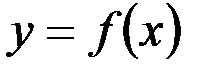 
, 
, где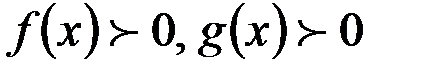 
, 
, 
, 
.
То её площадь вычисляется по формуле:
,
где предел интегрирования 
находят из уравнения 
.
5)Если криволинейная трапеция ограничена графиком функции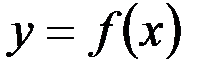 
, принимающей на отрезке интегрирования 
разные знаки
то её площадь вычисляется по формуле
,
где пределы интегрирования 
и 
находят из уравнения 
.
6) Площадь фигуры, ограниченной пересекающимися линиями 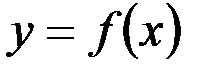и 
, где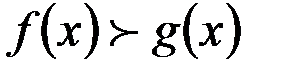 
(рис. 6),
находят по формуле
,
где пределы интегрирования 
и 
находят из уравнения 
.
В общем случае площадь фигуры, ограниченной линиями 
и 
находят по универсальной формуле
,
где пределы интегрирования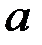 
и 
либо известны по условию задачи, либо их находят из уравнения .
Упражнения
Вычислить площадь фигуры, ограниченной линиями:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
РАЗДЕЛ 7. КОМПЛЕКСНЫЕ ЧИСЛА.
Понятие комплексного числа, алгебраическая форма записи комплексного числа. Действия с комплексными числами в алгебраической форме.
Комплексным числом 
называется выражение вида
,
где 
- действительные числа, 
- мнимая единица
.
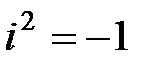- действительная часть комплексного числа 
,
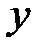- мнимая часть комплексного числа.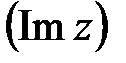 
|
|
|
Два комплексных числа 
и 
называются равными, если равны их действительные и мнимые части:
Два комплексных числа 
и 
, отличающиеся лишь знаком мнимой части, называются сопряженными.
Запись комплексного числа
,
называется алгебраической формой записи комплексного числа z.
Действия с комплексными числами в алгебраической форме записи.
Сложение
Суммой двух комплексных чисел и называется комплексное число, определяемое равенством:
Вычитание
Разностью двух комплексных чисел и называется комплексное число:
Умножение
Произведением комплексных чисел и называется комплексное число:
На практике, чтобы выполнить умножение комплексных чисел
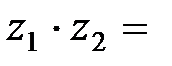
нужно раскрыть скобки, заменить 
, а затем привести подобные слагаемые.
Деление
Частное двухкомплексных чисел 
и 
находят по следующему правилу:числитель и знаменатель дроби 
умножают на число 
, сопряженное знаменателю, раскрывают скобки, заменяют 
, приводят подобные слагаемые и почленно делят числитель на знаменатель.
Возведение в степень комплексного числа и извлечение корня 
-ой степени из комплексного числа в алгебраической форме не выполняют.
Геометрическое изображение комплексного числа.
Комплексное число , изображают на координатной плоскости в виде радиус-вектора, конец которого имеет координаты 
Длина радиус-вектора называется модулем комплексного числа, обозначается 
и вычисляется по формуле:
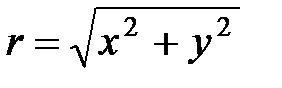
Угол, который радиус-вектор, изображающий комплексное число, образует с положительным направлением оси 
, называется аргументом комплексного числа и обозначается 
.
Аргумент комплексного числа удобно определять с помощью следующей таблицы:
| Четверть, в которой находится радиус-вектор, изображающий комплексное число | Формула для определения аргумента |
| I |
|
| II, III |
|
| IV |
|
|
|
|
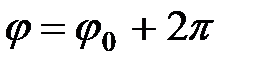
где 
определяют по формуле:
.
|
|
|
