 |
Общая схема исследования функции и построение её графика
|
|
|
|
Общее исследование функции и построение её графика удобно выполнять по следующей схеме:
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат (если это не представляется затруднительным).
3. Если область определения функции является симметричным числовым множеством, выяснить обладает ли функция свойством чётности или нечётности.
4. Найти асимптоты графика функции.
5. Найти промежутки монотонности и экстремумы функции.
6. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции.
7. По результатам исследования построить график функции.
Пример 1. Исследовать функцию 
и построить её график.
Решение.
1. 
;
2. График пересекает ось OY в точке с координатами 
3. Функция общего вида, т.к. 
.
4. График функции асимптот не имеет (т.к. функция является многочленом).
5. 
, 
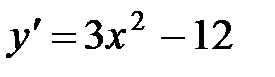- критические точки. Составим
таблицу:
|
| -2 |
|
| |
| + | - | + | ||
| функция возрастает | max | функция убывает | min -12 | функция возрастает |
Точка 
является максимумом функции, точка 
является минимумом функции.
6. 
. Составим таблицу:
|
|
| |
| - | + | |
| график выпуклый | график вогнутый |
Точка 
является точкой перегиба графика.
П ос троим график функции, используя результаты исследования (рис.3)
|
| -2 |
| -12 |
| х |
| у |
Рис.3
Пример 2. Исследовать функцию 
и построить её график.
Решение.
1. 
.
2. График функции пересекает оси координат в точке 
.
3. Функция нечётная, т.к. 
. График
функции симметричен относительно начала координат.
|
|
|
1. Найдём асимптоты графика функции.
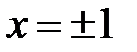- горизонтальные асимптоты, т.к. 
.
,
следовательно, наклонная асимптота выродилась в горизонтальную 
.
2. Найдём промежутки монотонности и экстремумы функции:
.
Данная дробь не может быть равна 0, т.к. числитель дроби всегда есть число положительное, следовательно, функция экстремумов не имеет.
Т.к. числитель и знаменатель дроби могут принимать только положительные значения, то при любых значениях 
производная может быть только положительной, следовательно, функция возрастает во всей своей области определения.
6. Найдём промежутки выпуклости и вогнутости и точки перегиба графика функции:
.
|
|
|
|
| |
| + | - | + | - | |
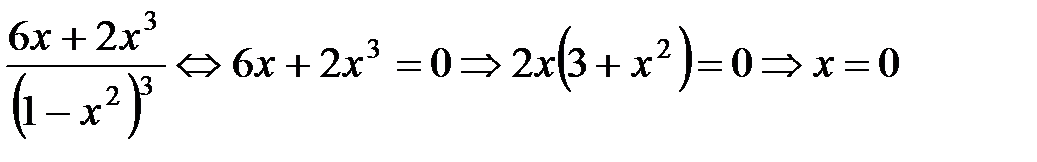| график вогнутый | график выпуклый | график вогнутый | график выпуклый |
Точка 
является точкой перегиба графика функции.
По результатам исследования построим график функции (рис. 4)
| -1 |
|
| х |
| у |
Рис. 4
Пример 3. Исследовать функцию 
Решение.
1. 
.
2. График пересекает оси координат в точке (0;0).
3. Функция общего вида, т.к. 
не является симметричным числовым множеством.
4. Найдем асимптоты графика функции, т.к. в точке 
функция претерпевает бесконечный разрыв, то график функции имеет вертикальную асимптоту . Для отыскания наклонной асимптоты найдем следующие пределы:
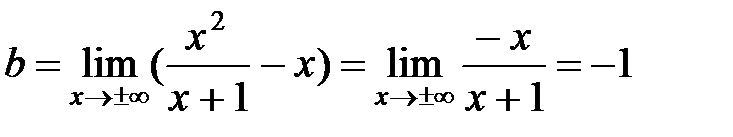
Таким образом, прямая 
служит наклонной асимптотой графика.
5. Найдем первую производную функции:
.
Найдем критические точки функции:
|
|
|
|
|
|
| |
| + | - | - | + | ||
|
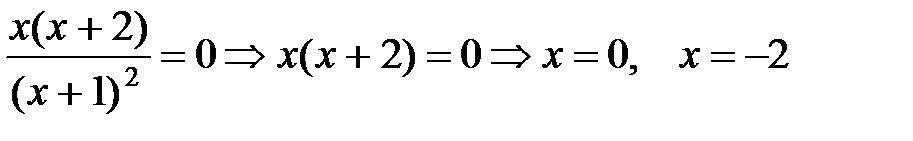
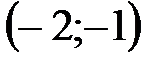
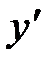
| функция возрастает |
max
| функция убывает | функция убывает | min | функция возрастает |
Точка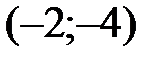 
является максимумом функции;
точка 
- является минимумом функции.
|
|
|
6. Найдем промежутки выпуклости и вогнутости и точки перегиба графика функции:
. 
Т.к. вторая производная функции не равна 0, то точек перегиба у графика функции нет.
Найдём интервалы выпуклости и вогнутости графика функции:
|
|
|
| - | + |
| график выпуклый | график вогнутый |
По результатам исследования построим график функции (рис. 5)
| у |
| х |
| х=1 |
| у=х-1 |
| (-2;-4) |
Рис.5
Упражнения.
№1. Исследовать функцию и построить её график:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
РАЗДЕЛ5. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
5.1. Неопределённый интеграл: основные понятия, определения, свойства
Определение.
Функция 
называется первообразной для функции 
на некотором промежутке 
, если для всех значений 
из этого промежутка выполняется
.
Рассмотрим примеры.
1. Функция 
является первообразной для функции 
на всей числовой оси, т.к. при любом значении 
выполняется
.
2. Функция 
является первообразной для функции 
для любого 
, т.к.
.
Основной задачей дифференциального исчисления является нахождение производной заданной функции. Разнообразные вопросы математического анализа и его многочисленные приложения в геометрии, механике, физике и технике приводят к обратной задаче: по данной функции 
найти такую функцию 
, производная которой была бы равна функции , т.е.
.
Восстановление функции по её производной - основная задача интегрального исчисления.
Задача нахождения по данной функции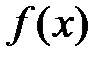 
называется интегрированием.
Действительно, если 
- первообразная для 
, т.е.
,
то функция 
, где 
- произвольная постоянная, также является первообразной для 
, т.к.
для любого числа 
.
Например, для функции 
первообразной является не только функция 
, но и функция 
, т.к.
.
Теорема.
Если функция 
является первообразной для функции 
на некотором промежутке 
, то функция
,
где 
- произвольная постоянная, также является первообразной для 
на этом же промежутке.
Определение.
Совокупность всех первообразных для функции 
, определённых на некотором промежутке, называется неопределённым интегралом от функции 
на этом промежутке и обозначается символом
.
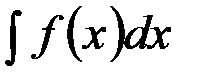Читается: «интеграл от эф от икс де икс».
|
|
|
По определению
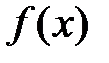- подынтегральная функция,
- подынтегральное выражение,
- переменная интегрирования,
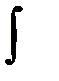- знак неопределённого интеграла,
С - постоянная величина (константа).
Нахождение неопределённого интеграла по данной подынтегральной функции называется интегрированием этой функции.
Так как интегрирование представляет собой операцию, обратную дифференцированию, то для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
|
|
|
