 |
Методические указания по выполнению и оформлению контрольной работы
|
|
|
|
Выполнение контрольной работы включает в себя решение семи заданий по своему номеру варианта. Номер варианта соответствует порядковому номеру студента по учебному журналу.
Контрольная работа должна быть оформлена в отдельной 12 листовой тетради в клетку, аккуратно, разборчиво. Обложка тетради должна иметь титульный лист установленной формы.
К каждому заданию необходимо записывать условие.
В задании №1 при нахождении определителей все вычисления должны быть записаны.
В задании №3 при нахождении производных функции делать упрощения и преобразования с вычисленными производными не обязательно, если получились большие выражения.
При решении задания №4 необходимо исследовать функцию по общей схеме, сделать чертеж.
При решении задания №6 необходимо сделать чертеж к задаче, заштриховать искомую площадь, сделать подробные вычисления.
При решении задания №7 (б) действия с комплексными числами выполнять в тригонометрической или показательной формах.
Выполненная контрольная работа должна быть сдана на заочное отделение. Контрольная работа регистрируется и передается преподавателю для рецензирования и оценивается «зачет» или «незачет».
К экзамену по дисциплине студент допускается только в том случае, если у него зачтена контрольная работа.
КОНТРОЛЬНАЯ РАБОТА
Задание 1.
Решить систему а) по формулам Крамера.
Б) методом Гаусса.
1. 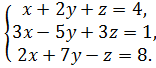 2.
2. 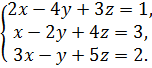
3. 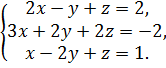 4.
4. 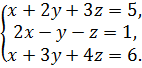
5. 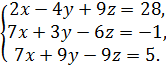 6.
6. 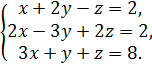
7. 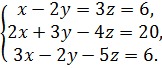 8.
8. 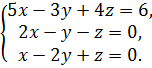
9. 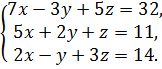 10.
10. 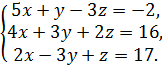
Задание 2.
Вычислить пределы.
1. а) 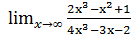 б)
б) 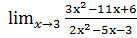 ;
;
в) 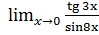
2. а)  б)
б) 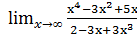
в) 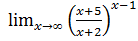
3. а) 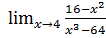 б)
б) 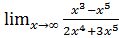
в) 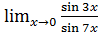
4. а) 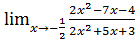 б)
б) 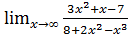
в) 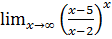
5. а) 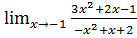 б)
б) 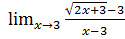
в) 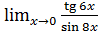
6. а) 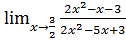 б)
б) 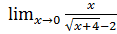
в) 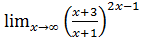
7. а) 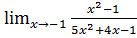 б)
б) 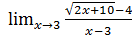
в) 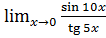
8. а) 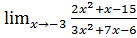 б)
б) 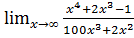
в) 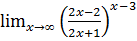
9. а) 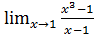 б)
б) 
в) 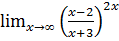
10. а) 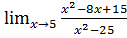 б)
б) 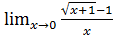
в) 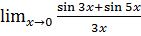
Задание 3.
Найдите производные функций.
|
|
|
1.а) y = 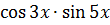 б) y =
б) y = 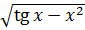
в) y = 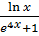
2. а) y = 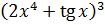 б) y =
б) y = 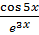
в) y = 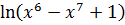
3. а) y = 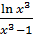 б) y =
б) y = 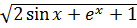
в) y = 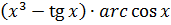
4. а) y = arc 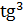 x б) y =
x б) y = 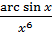
в) y = 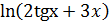
5. а) 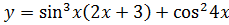 б)
б) 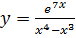
в) y = 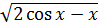
6. а) y= 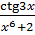 б) y =(2
б) y =(2 
в) y = 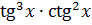
7. а) у = 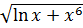 б) у =
б) у = 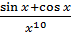
в) у =(2 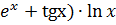
8. а) у = 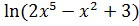 б) у =
б) у = 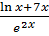
в) y = 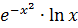
9. а) у = 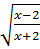 б) y =
б) y = 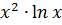
в) y =(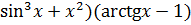
10. а) у = 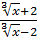 б) у =
б) у = 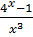
в) у = 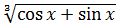
Задание 4.
Исследовать и построить график функции.
1. у = 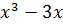
2. y = 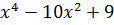
3. y = 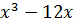
4. y = 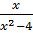
5. y = 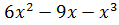
6. y = 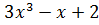
7. y = 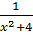
8. y = 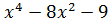
9. y = 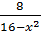
10. y =- 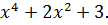
Задание 5.
Найти неопределённые интегралы.
1. а) 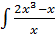 dx б)
dx б) 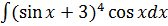
в) 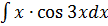
2. а) 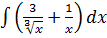 б)
б) 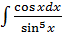
в) 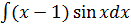
3. а) 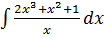 б)
б) 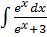
в) 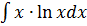
4. а) 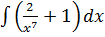 б)
б) 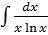
в) 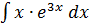
5. а) 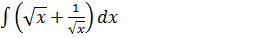 б)
б) 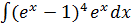
в) 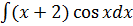
6. а) 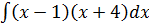 б)
б) 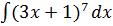
в) 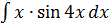
7. а) 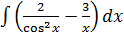 б)
б) 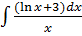
в) 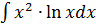
8. а) 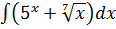 б)
б) 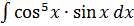
в) 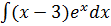
9. а) 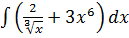 б)
б) 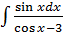
в) 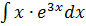
10. а) 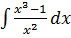 б)
б) 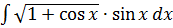
в) 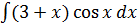
Задание 6.
Вычислить площадь фигуры, ограниченной линиями.
1. y = 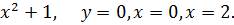
2. y = 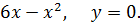
3. y = 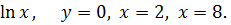
4. y = 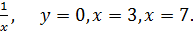
5. y = 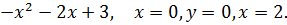
6. y = 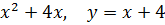 .
.
7. y = 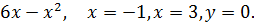
8. y =  ,
, 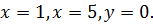
9. y = 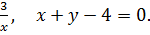
10. y = 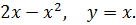
Задание 7.
Выполнить действия с комплексными числами.
1. а) 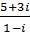 б)
б) 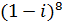
2. а) 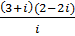 б)
б) 
3. а) 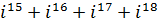 б)
б) 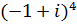
4. а) 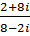 б)
б) 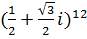
5. а) 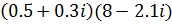 б)
б) 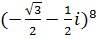
6. а) 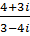 б)
б) 
7. а) 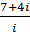 б)
б) 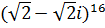
8. а) 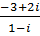 б)
б) 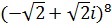
9. а) 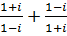 б)
б) 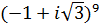
10. а) 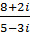 б)
б) 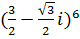
Задание 8.
Исследовать на сходимость ряд.
1) а) 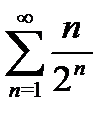 б)
б) 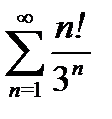
2) а) 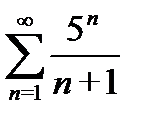 б)
б) 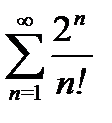
3) a) 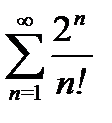 б)
б) 
4) a) 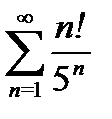 б)
б) 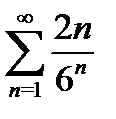
5) а) 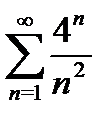 б)
б) 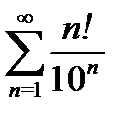
6) а) 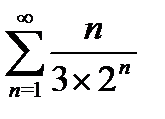 б)
б) 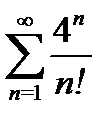
7) а) 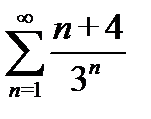 б)
б) 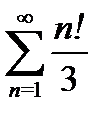
8) а) 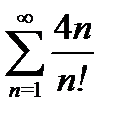 б)
б) 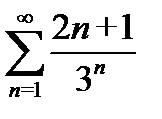
9) а) 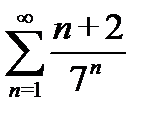 б)
б) 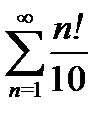
10) а) 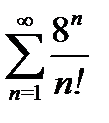 б)
б) 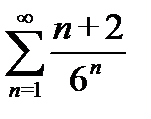
ЛИТЕРАТУРА
Основные источники:
1. Богомолов Н.В., Самойленко П.И. Математика, (учебник для ссузов) - М: Дрофа, 2010.
2. Богомолов Н.В. Сборник задач по математике, (учебное пособие для ссузов) – М: Дрофа, 2010.
3. Богомолов Н.В. Математика. Дидактические задания (учебное пособие для ссузов) - М.: Высшая школа, 2010.
4. Яковлев Г.Н. (под ред.) Математика, в 2-х книгах, (учебник для ссузов) - ИД «Оникс», 2011.
Дополнительные источники:
1. Алексеева Е.В. Дифференциальное исчисление функции двух переменных: учебное пособие для студентов 1-го и 2-го курса технических специальностей по разделу дисциплины «Математика».
2. Алексеева Е.В. Дифференциальное исчисление функции одной переменной: учебное пособие для студентов 1-го и 2-го курса технических специальностей по разделу дисциплины «Математика».
3. Алексеева Е.В. Основы линейной алгебры: учебное пособие для студентов 2-го курса технических специальностей по разделу дисциплины «Элементы высшей математики», «Математика».
|
|
|
4. Письменный Д.Т. Конспект лекций по высшей математике: полный курс –М: Айрис-пресс, 2006.
5. www.exponenta.ru – образовательный математический сайт.
ПРИЛОЖЕНИЯ
Приложение 1
Формулы сокращённого умножения
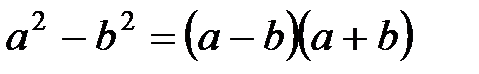 - разность квадратов
- разность квадратов
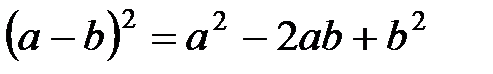 - квадрат разности
- квадрат разности
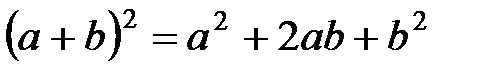 - квадрат суммы
- квадрат суммы
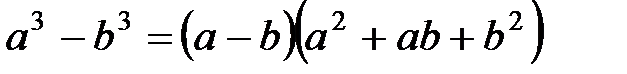 - разность кубов
- разность кубов
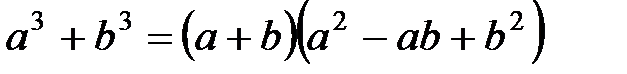 - сумма кубов
- сумма кубов
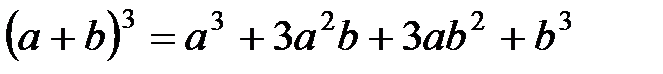 - куб суммы
- куб суммы
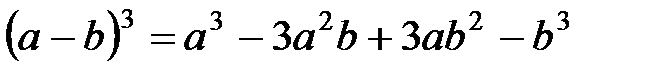 - куб разности
- куб разности
Формула разложения квадратного трёхчлена на линейные множители
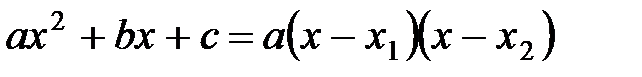 ,
,
где 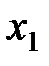 и
и 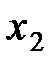 - корни квадратного уравнения
- корни квадратного уравнения 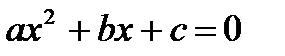 .
.
Приложение 2
Правила дифференцирования
 .
.


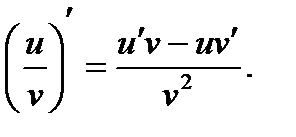
Таблица производных элементарных функций.
1. 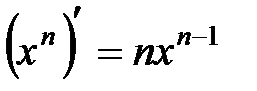 , в частности
, в частности 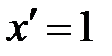 ,
, 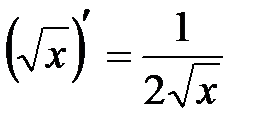 ,
, 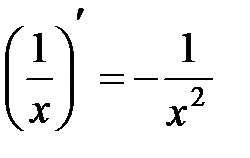 ,
, 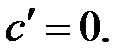
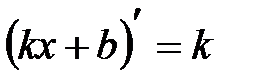 .
.
2. 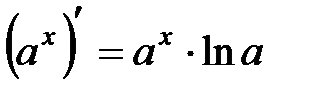 , в частности
, в частности  .
.
3. 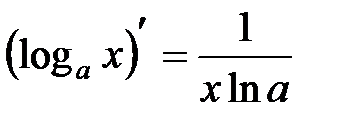 , в частности
, в частности 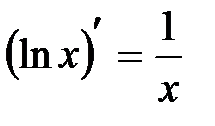 .
.
4. 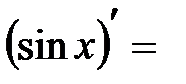
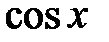 .
.
5. 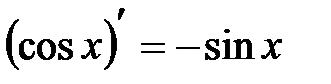 .
.
6. 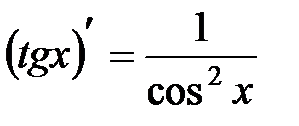

7. 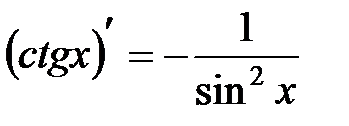 .
.
8. 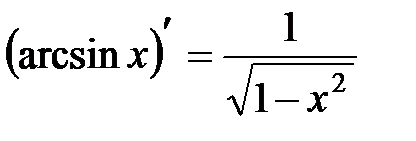 .
.
9. 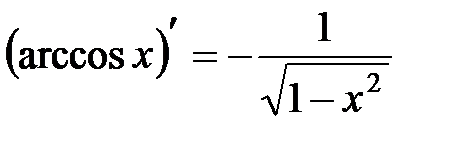
10. 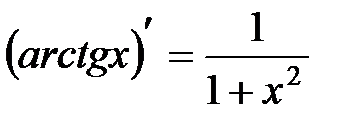
11. 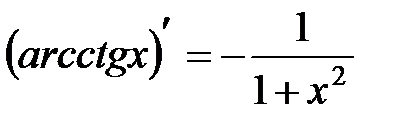
Приложение 3
Таблица производных сложных функций
1. 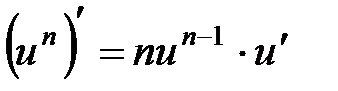 , в частности
, в частности 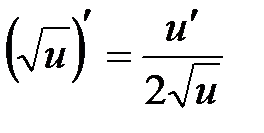 ,
, 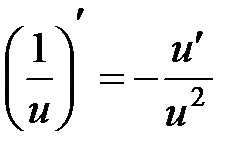 ,
,
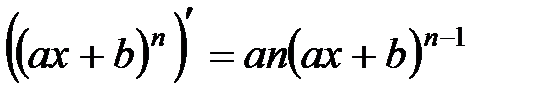
2. 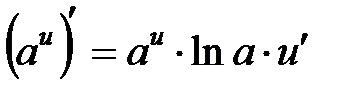 , в частности
, в частности 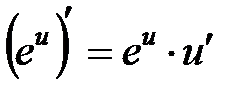 .
.
3. 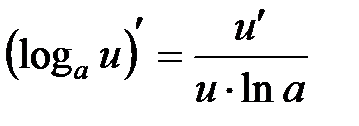 , в частности
, в частности 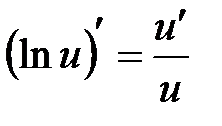 .
.
4. 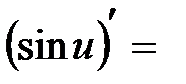
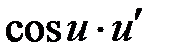 .
.
5. 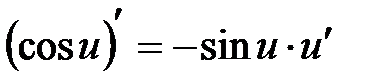 .
.
6. 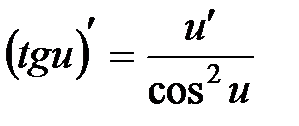
7. 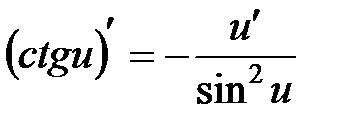 .
.
8. 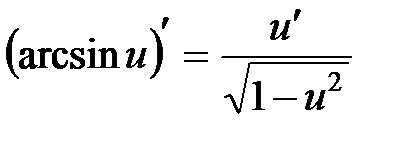 .
.
9. 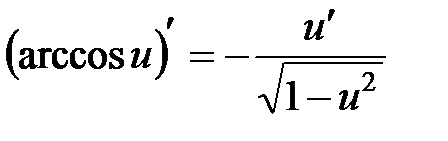
10. 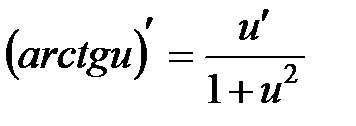
11. 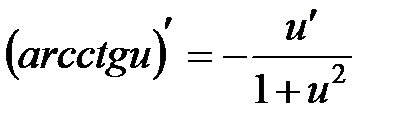
Приложение 4
|
|
|


