4. Задачина сообразительность. Занятие 17. 1. Размещение фигур. 2. Дидактическая игра «В зоопарке». 3. Действия с числами

4. Задачина сообразительность

1. Полевая гвоздика, цикорий, водяная лилия раскрывают свои цветки в пять, восемь, девять часов. Из них водяная лилия раскры­вает венчики своих цветков в восемь часов, полевая гвоздика - на час позже. В какое время раскрываются цветки полевой гвоздики?

2. Трое играли в шашки. Всего сыграли три партии. Сколько партий сыграл каждый? (Две партии. )

3. По двору ходят куры и кролики, у всех вместе 20 голов и 52 ноги. Сколько кур и кроликов во дворе? (6 кроликов и 14 кур. )

Решать методом подбора.

Занятие 17

1. Размещение фигур

Дидактическая игра «Кружочки в квадратах».

Дидактическая цель: формирование у учащихся навыков построения различных комбинаций

Образец задания:

Инструкция: нарисуйте кружочки в последних квадратах так, чтобы сохранилась закономерность чередования кружочков при их размещении.

Организация выполнения задания:

1. Учитель на доске готовит рисунки 1, 2, 3, 4.

2. Дети в тетрадях чертят квадрат, рис. 4, и заполняют его кру­жочками со штриховкой.

2. Дидактическая игра «В зоопарке»

Дидактическая цель: закрепление приемов сложения и вычитания двузначных чисел с переходом через десяток. Образец задания:

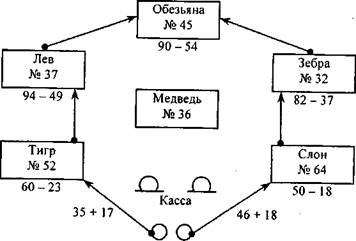
Организация выполнения задания:

Учитель на доске схематично изображает клетки животных, под ними записывает примеры, а на клетках - номера.

Содержание игры:

Учитель сообщает детям, что два ученика (Дима и Коля) в вос­кресный день отправились в зоопарк. После путешествия по зоо­парку они сочинили интересную игру. Они зашифровали свой путь от клетки к клетке примером. Ответ примера и номер одной из клеток совпадают. Они начали свое путешествие от билетной кассы, которая зашифрована двумя примерами, определяющими направ­ления движения каждого ученика.

 

У одной из клеток ученики встретились. Необходимо определить, где ученики встретились. На­правление движения каждого ученика надо обозначить стрелками.

Учитель вызывает поочередно учеников из каждого ряда, они, решив пример правильно, показывают стрелкой путь движения каждого ученика и место их встречи.

Выигрывает та команда, которая не допускает ошибок при оп­ределении маршрута по зоопарку.

3. Действия с числами

Формирование вычислительных навыков.

1. Даны ряды чисел:

1  2  3    4     5

6     7  8    9     10

11    12  13   14    15

Сумма чисел первого вертикального ряда 18. Быстро найдите суммы остальных четырех вертикальных рядов.

2. На доске записаны четыре примера:

36 + 18+12                          24 + 37 + 16

47 + 35 + 3                          47 + 38 + 13

Каким образом можно быстро написать ответы? (Надо восполь­зоваться перестановкой и группировкой слагаемых).

4. Занимательные задачи

1. Мама купила яблоки и груши. Когда её' спросил сын, сколько груш и сколько яблок она купила, мама ответила: «Всего фруктов 25, пятая часть из них - груши, остальные - яблоки. А теперь сам сосчитай, сколько груш и сколько яблок».

2. Ребята задавали друг другу интересные задачи. Один маль­чик вышел к доске и записал подряд семь цифр: 1, 2, 3, 4, 5, 6, 7 - и сказал: «Кто из вас сумеет записать этими цифрами 4 числа так, чтобы они в сумме составили число 100 и, чтобы каждая цифра употреблялась один раз, тот сегодня будет считаться лучшим ма­тематиком».

Занятие 18

1. Дидактическая игра «Треугольник из треугольников»

Дидактическая цель: формирование умения быстро и правильно складывать однозначные и двузначные числа. Образец задания:

Ответ:

а) 1 + 5 + 6 + 8 = 20            6 )7+ 1 + 3+ 6 = 17

5 + 2+9 + 4 = 20                  1 + 9 + 2 + 5 = 17

Правила и игровые действия:

Данные треугольники составлены из 9 маленьких треугольни­ков, в которые вписаны числа. Найдите суммы чисел в треугольни­ках, составленных из четырех маленьких треугольников. Мы ви­дим, что сумма чисел в каждом треугольнике, который образован четырьмя маленькими треугольниками, представляет собой одно и то же число. Такие треугольники мы будем называть магическими. В данных примерах были использованы одни и те же последова­тельные числа (от 1 до 9), а полученные суммы различны (для пер­вого треугольника это 20, для второго - 17). При перестановке этих же чисел мы сможем получить подобные треугольники (магиче­ские), но суммы чисел, записанные в них, будут другими, отли­чающимися от 17 и 20 (например, 25).

Являются ли эти треугольники магическими?

 

 

а)                                    6)                                                в)

 6 +12 + 13 + 7 = 38 11+5 + 4+10 = 30      7 + 8 + 9 + 5 = 29

  12 + 15 + 9 + 2 = 38   5 + 2 + 7 + 16 = 30      8 + 2 + 1 + 6 = 17

  13 + 9 + 10 + 6 = 38  4 + 7 + 6+13=30 9 + 1 + 3 + 4 = 17

 

             да                                 да                                     нет

⇐ Предыдущая53545556575859606162Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: