Главная | Обратная связь | Поможем написать вашу работу!

Задачи для самостоятельной работы

⇐ ПредыдущаяСтр 3 из 19Следующая ⇒

1.Что такое числовая матрица? Могут ли все элементы матрицы равняться нулю?

2.Какие матрицы называются равными? Равны ли матрицы

и ?

3.Как сложить две матрицы? Можно ли сложить две матрицы с размерами 2´3 и 3´2?

4.Как вычесть из одной матрицы другую? Можно ли из матрицы А вычесть эту же матрицу А? Что получится?

5.Докажите, что: а) А + В = В + А; б) А – В = А + (-1)В.

6.Какая матрица называется транспонированной по отношению к матрице А? Для любой ли матрицы А существует транспонированная?

7.Может ли выполняться равенство А^Т = А? Ответ обоснуйте.

8.Для каких матриц А и В определено произведение АВ? Как вычисляются элементы матрицы АВ?

9.Известно, что (1 2 3) × А = (0 1). Каковы размеры матрицы А?

10. Можно ли умножить строку с n элементами на столбец с n элементами? Что получится?

11. Всегда ли выполняется равенство:

а) А(ВС) = (АВ)С; б) АВ = ВА; в) (А + В)С = АС + ВС?

12. Что такое единичная матрица? Является ли единичной матрица:

а) б) в)

13. Дайте определение обратной матрицы.

14. Опишите способ нахождения обратной матрицы с помощью элементарных преобразований.

15. Справедливы ли равенства:

1) (А^Т)^-1 = (А^-1)^Т; 2) (aА)^-1 = a^-1 А^-1; 3) (АВ)^-1 = В^-1 А^-1;

4) (АВС)^-1 = С^-1 В^-1 А^-1; 5) (А^-1)^k = (А^k)^-1; 6) (А + В)^-1 = А^-1 + В^-1

16. Какая матрица называется основной и какая – расширенной матрицей системы линейных уравнений?

17. Какая система уравнений называется совместной?

18. Сформулируйте необходимое и достаточное условие совместности системы линейных уравнений?

19. Какая система уравнений называется квадратной?

20. При каком условии квадратная система линейных уравнений имеет единственное решение?

21. В чем суть метода Гаусса (метода последовательного исключения неизвестных)?

22. Что называется подстановкой n-ой степени?

23. Какая подстановка n-ой степени называется четной, нечетной? Что такое транспозиция?

24. Каким образом определяется знак подстановки?

25. Объясните, что такое определитель n-го порядка. Из скольких слагаемых он состоит?

26. Записать формулу для вычисления определителей второго порядка, третьего порядка.

27. Вычислите устно определители и .

28. Чему равен определитель треугольной, диагональной матрицы?

29. Известно, что =1. Чему равен ?

30. Известно, что А- матрица размерности 5×5 и =3. Чему равен ?

31. Перечислите основные свойства определителей.

32. Что значит: разложить определитель по элементам данного столбца (строки)?

33. Объясните, что такое алгебраическое дополнение данного элемента а_ij определителя? Чему равно алгебраическое дополнение элемента а₁₂ матрицы (а_ij)_2х2?

34. Объясните, что такое минор данного элемента а_ij матрицы. Чему равен минор элемента а₁₂ матрицы (а_ij)_2х2?

35. Как связаны между собой алгебраическое дополнение и минор данного элемента?

36. Напишите формулу для вычисления элементов обратной матрицы. Составьте обратную матрицу для матрицы .

37. Напишите выражение для решения квадратной системы линейных уравнений с невырожденной матрицей по формулам Крамера.

38. Даны матрицы и .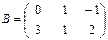

Найти: а) А + В; б) 2В; в) В^Т; г) А×В^Т; д) В^Т× А.

39. Доказать, что если

АВ = ВА, то (А + В) = А² + 2АВ + В².

40. Вычислить произведение матриц:

а)

;

б)

41. Найдите значение многочлена ƒ(х) = х² + х + 2 от матрицы А, т.е. вычислите ƒ(А) = А² + А + 2Е, где Е – единичная матрица подходящего размера

а) А = б) В=

42. Вычислите

43. Найти все матрицы коммутативные с матрицей А: А = .

44. Решить методом Гаусса следующие системы линейных уравнений:

а) 2х₁ - х₂ + х₃ - х₄ = 1 2х₁ - х₂ - 3х₄ = 2 3х₁ - х₃ + х₄ = -3 2х₁ + 2х₂ - 2х₃ + 5х₄ = -6	3х₁ + 4х₂ - 5х₃ + 7х₄ = 0 д) 2х₁ - 3х₂ + 3х₃ - 2х₄ = 0 4х₁ + 11х₂ - 13х₃ + 16х₄ = 0 7х₁ - 2х₂ + х₃ + 3х₄ = 0
х₁ - 2х₂ + 3х₃ - 4х₄ = 4 б) х₂ - х₃ + х₄ = -3 х₁ + 3х₂ - 3х₄ = 1 -7х₂ + 3х₃ + х₄ = -3	2х₁ - х₂ + х₃ - х₄ = 1 е) х₁ + 3х₂ - х₃ - х₄ = 0 3х₁ - 2х₂ + 2х₃ - 3х₄ = -1 х₁ + х₂ - х₃ + х₄ = 2
х₁ + 2х₂ +3х₃ + 4х₄ = 11 в) 2х₁ + 3х₂ + 4х₃ + х₄ = 12 3х₁ + 4х₂ + х₃ + 2х₄ = 13 4х₁ + х₂ + 2х₃ + 3х₄ = 14	2х₁ - х₂ + х₃ - х₄ = 1 ж) х₁ + 3х₂ - х₃ - х₄ = 0 3х₁ - 2х₂ + 2х₃ - 2х₄ = 1 х₁ + х₂ - х₃ + х₄ = 2
х₁ + х₂ + 2х₃ + 3х₄ = 1 г) 3х₁ - х₂ - х₃ - 2х₄ = -4 2х₁ + 3х₂ - х₃ - х₄ = -6 х₁ + 2х₂ + 3х₃ - х₄ = -4	х₁ + 2х₂ + 4х₃ - 3х₄ = 4 з) 3х₁ + 5х₂ + 6х₃ - 4х₄ = 1 4х₁ - 5х₂ - 2х₃ + 3х₄ = 0 -3х₁ + 8х₂ + 24х₃ - 19х₄ = 1

45. Вычислите определители:

а) cos a - sin a б) -3 0 1 в) 2 1 3

sin cos a -5 2 4 5 3 2

0 3 7 1 4 3

г) д) е)

46. Решить уравнение над полем R:

47. Решить неравенство:

48. Не раскрывая определитель, докажите справедливость равенства:

49. Вычислите определитель:

а) ; б) ;

в) ; г) .

50. Вычислите определители n-го порядка:

а) б)

в) г) д)

е) ж)

51. Имеет ли матрица А = обратную? Если да, то найдите ее.

52. Вычислите обратную матрицу для матрицы А с помощью алгебраических дополнений

а) А= ; б) А=

53. При каких значениях параметров a и b для матрицы А существует обратная:

а) А= б) А=

54. Используя обратную матрицу, найдите матрицу Х, удовлетворяющую уравнению:

а) б) .

55. Решить систему линейных уравнений по формулам Крамера

2х₁ – х₂ – х₃ = 4 а) 3х₁ + 4х₂ – 2х₃ = 11 3х₁ – 2х₂ + 4х₃ = 11	х₁ + х₂ + 2х₃ = -1 б) 2х₁ – х₂ + 2х₃ = -4 4х₁ + х₂ + 4х₃ = -2
3х₁ + 2х₂ + х₃ = 5 в) 2х₁ + 3х₂ + х₃ = 1 2х₁ + х₂ + 3х₃ = 11	х₁ + 2х₂ + 3х₃ + 4х₄ = 5 г) 2х₁ + х₂ + 2х₃ + 3х₄= 1 3х₁ + 2х₂ + х₃ + 2х₄= 1 4х₁ + 3х₂ + 2х₃ + х₄= -5