 |
Основные алгебраические структуры
|
|
|
|
Основным понятием современной математики является понятие алгебраической структуры, в частности, группы. Теория групп – это математическая дисциплина, предметом которой является, по существу, симметрия – понятие, охватывающее массу явлений окружающего нас мира и имеющее чрезвычайно важное значение в науке, технике и искусстве.
Определение 1.1.
Отношение, при котором каждой упорядоченной паре (a, b) элементов множества М ставится в соответствие единственный элемент с из этого же множества, называется бинарной алгебраической операцией, определяемой на множестве М.
Бинарные алгебраические операции обозначают значком: *, °. Записывают: a ° b=c или a * b=c. Элемент с называют результатом бинарной алгебраической операции или композицией элементов a и b.
Кроме бинарных алгебраических операций существуют и нульместные (нульарные), унарные, тернарные,… n -арные операции.
Нульместной алгебраической операцией на множестве М называется выделение (фиксация) какого-нибудь элемента множества.
Если каждому элементу из М соответствует другой (или тот же) элемент из М, то операция называется унарной. Унарную операцию называют также оператором.
Операция, при которой n элементам из множества М соответствует единственный элемент из М, называется n-арной или операцией ранга n.
Примеры бинарных алгебраических операций:
На множестве целых чисел сумма и разность любых двух целых чисел есть целое число, значит данные операции являются бинарными алгебраическими операциями на множестве целых чисел.
Алгебраическую операцию можно задать посредством текстового описания закона, по которому из двух данных элементов получается третий.
|
|
|
Во-вторых, для небольших конечных множеств операцию можно задать с помощью таблиц Кэли, названных в честь выдающегося математика XIX века. Эти таблицы составляются следующим образом: на пересечении строки а и столбца b ставится значение результата.
Алгебраическая операция * на множестве М называется ассоциативной, если для любых трёх элементов a, b, c, принадлежащих множеству М, выполняется равенство: (a*b)*c=a*(b*c).
Алгебраическая операция * на множестве М называется коммутативной, если ("a, bÎM) a*b=b*a.
Пусть задано множество М с двумя бинарными алгебраическими операциями *, °.
Бинарная операция * называется дистрибутивной относительно операции °, если ("a, b, cÎG) (a° b)*c=(a*с)° (b*c) – правая дистрибутивность;
с* (a ° b) =(с*а) ° (с*b) –левая дистрибутивность.
Элемент n ÎМ называется нейтральным элементом относительно бинарной операции *, если длялюбого элемента a ÎМ выполняется равенство a*n=n*a=a.
Необходимость двух равенств в определении продемонстрируем на следующем примере: Во множестве действительных чисел без нуля рассмотреть операцию деления. Назвать нейтральный элемент.
Согласно определению нейтрального элемента ("aÎR) a:1=a – верно и 1:a=1/a¹a, то есть элемент 1 не является нейтральным элементом. Это происходит из-за того, что операция деления во множестве R некоммутативная. Именно из-за возможного свойства некоммутативности в определении нейтрального элемента необходимы два равенства.
Поскольку существуют некоммутативные операции, то введём следующие определения:
Элемент n/ называется левым нейтральным элементом операции *, если ("aÎM) n/*a=a.
Аналогично, n// ÎМ называется правым нейтральным элементом относительно операции *, если ("aÎM) a*n//=a.
Элемент a/ ÎM называется симметричным элементу a ÎM, если a*a/=a/*a=n.
Теорема 1.1. Если алгебраическая система (G,*) обладает нейтральным элементом n, то он единственный.
|
|
|
Теорема 1.2. Если n/ – левый нейтральный элемент, n// – правый нейтральный элемент в G, то n/=n//.
Пример 1.1. Доказать, что во множестве К, содержащем не менее двух элементов, на котором формулой a ° b = b задана бинарная операция, не существует нейтрального элемента.
Доказательство (методом от противного).
Пусть в К существует нейтральный элемент n, и пусть а – любой элемент из К. По определению нейтрального элемента a ° n = a, а по условию задания операции имеем: a ° n = n. Правые части подчеркнутых равенств равны, следовательно a = n, т.е. множество К содержит больше двух элементов. Значит наше предположение неверно, а верно то, что требуется доказать.
Определение 1.2.
Группой G называется множество с одной бинарной алгебраической операцией *, обладающей следующими свойствами:
1) ("a, b, cÎG) a*(b*c)=(a*b)*c;
2) ($nÎG)("aÎG) a*n=n*a=a;
3) ("aÎG)($a/ÎG) a/*a=a*a/=n.
Операция *, удовлетворяющая свойствам 1)-3), иногда называется групповой операцией, а элементы множества G – элементы группы.
Свойством коммутативности группа может не обладать. Если же в группе выполняется свойство коммутативности для любых элементов, то она называется коммутативной или абелевой.
Введем следующие определения:
· Множество с алгебраической операцией называют группоидом.
· Группоид с ассоциативной операцией называют полугруппой.
· Полугруппу с нейтральным элементом называют моноидом.
Связь между данными алгебраическими структурами прекрасно иллюстрирует рисунок, из которого видно, что любая группа является полугруппой, а любая полугруппа является группоидом.
Группы бывают конечные и бесконечные. Число элементов конечной группы G называется ее порядком и обозначается ½ G ½.
Простейшие свойства групп (на мультипликативном языке):
1) В каждой группе существует только одна единица (по теореме о единственности нейтрального элемента);
2) В каждой группе любой элемент g имеет единственный ему обратный элемент g-1 ÎG;
3) Во всякой группе каждое из уравнений ax=b и ya=b при любых a, bÎG имеет решение и притом только одно;
4) Справедливы законы сокращения:
( " a, b, с ÎG) ab=cbÞ a=c (сокращение справа),
( " a, b, с ÎG) ba=bcÞ a=c (сокращение слева).
5) ( " a, bÎG) ab=a Þ b=1 и ( " a, bÎG) ba=a Þ b=1;
|
|
|
6) ( " a, bÎG) ab=1 Þ a-1 =b Ù b-1 =a;
7) В группе имеет место обобщенный закон ассоциативности, а если группа абелева – обобщенный закон коммутативности.
8) ( " aÎG) (a-1) -1=a;
9) ( " a1, a2,… an ÎG) (a1 a2… an) -1= (an) -1(an-1) –1 (a1) –1
Определение 1.3.
Непустое подмножество H группы (G,◦) называется подгруппой группы G, если оно само является группой относительно той же операции, что и группа G.
Критерий подгруппы: Непустое подмножество H группы G является подгруппой группы G тогда и только тогда, когда:
1) ("a, bÎH) a bÎH; 2) ("aÎH) (a-1) ÎH.
Примеры подгрупп:
1. Тривиальные (несобственные) подгруппы. Каждая группа имеет единичную подгруппу и сама является своей подгруппой.
2. Циклические подгруппы. Зафиксируем элемент a в группе G. Подмножество [ a ] = {ak /kÎZ)} группы G, состоящее из всевозможных степеней элемента a, является подгруппой в G, порожденной элементом а, который называется образующим своей циклической подгруппы [ a ].
Одним из важных понятий в теории групп является понятие гомоморфизма.
Определение 1.4. Пусть имеется две группы (G1,◦) и (G2,*).
Отображение f: G1®G2 называется гомоморфизмом групп, если:
("g1, g2ÎG1) f(g1◦g2)=f(g1)*f(g2).
Определение 1.5. Отображение f: G1®G2 называется изоморфизмомгрупп (G1,◦) и (G2,*), если:
а) f - взаимно однозначное соответствие между множеством элементов первой группы и множеством элементов второй группы;
б) ("g1, g2ÎG1) f(g1◦g2)=f(g1)*f(g2).
Понятие гомоморфизма является обобщением понятия изоморфизма.
Мономорфизм – гомоморфизм, являющийся одновременно инъективным отображением.
Эпиморфизм – гомоморфизм, являющийся одновременно сюръективным отображением.
Теорема 1.3. Если группы G1 и G2 изоморфны, то любое свойство группы G1 переносится на группу G2 и обратно.
Определение 1.6.
Ядром гомоморфизма групп называют множество элементов группы G1, чей образ совпадает с нейтральным элементом группы G2 .
Обозначение: Ker f = {g1ÎG1 / f(g1)=e2}=f -1(e2).
Определение 1.7.
Образом гомоморфизма f называют множество элементов из G2,
имеющих прообразы в G1.
Обозначение: Im f = f(G1)={g2ÎG2 /($ g1ÎG1) g2=f(g1)}.
|
|
|
Основные свойства гомоморфизма групп:
1. Гомоморфный образ группы также является группой относительно своей операции.
2. Пусть f: G1®G2 – гомоморфизм групп. Тогда
а) f(1)=1 и f(а-1)=(f(а))-1
б) Ker f – подгруппа группы G1
в) Im f - подгруппа группы G2
г) f - мономорфизм тогда и только тогда, когда Ker f = {е1};
д) f - эпиморфизм тогда и только тогда, когда Im f = G2
е) если f – изоморфизм, то f -1 : G2®G1 также изоморфизм.
3. Композиция любых двух (или нескольких) гомоморфизмов (моно, эпи) является гомоморфизмом (моно, эпи).
Примеры гомоморфизмов групп:
· Пусть G – произвольная группа, аÎG – фиксированный элемент. Отображение группы G в себя определено формулой x®axa-1 для любого хÎG. Заданное отображение - автоморфизм группы G, называемый внутренний.
· Отображение j: (R,+) ®(R+, ×), заданное формулой j(x)= a, где а – фиксированный элемент из множества R\{1}, является изоморфизмом между аддитивной и мультипликативной группами, причем обратным к нему служит изоморфизм j-1: (R+, ×) ®(R, +), j-1(х )= log  x.
x. 
Определение 1.8. Алгебра (К, +, ∙) – кольцо, если
1. (К, +) – абелева группа.
2. (К, ∙) – полугруппа.
3. Умножение дистрибутивно относительно сложения.
Кольцо с единицей (т.е. нейтральным элементом относительно умножения) называется унитарным. Если умножение коммутативно, то кольцо называется коммутативным.
Свойства колец:
I. Так как (К, +)- абелева группа, то справедливы все свойства групп.
II. Характеристические свойства:
1. 0 ∙ а = а ∙ 0 = 0 (нуль является поглощающим элементом).
2. Правило знаков: (-а) ∙ в = (-а в); а (-в) = (-а в); (-а) (-в) = ав.
3.  ("a, b ÎК) а (в - с) = ав – ас дистрибутивность умножения
("a, b ÎК) а (в - с) = ав – ас дистрибутивность умножения
(в - с) а = ва –са относительно вычитания
Пусть К – коммутативное кольцо с единицей. В кольце К можно определить отношение делимости.
Определение 1.9. а  в
в  $qÎK, что а = в·q
$qÎK, что а = в·q
Определение 1.10. Элемент ε кольца К называется обратимым, если в кольце К существует такой элемент ε 1, что ε · ε 1 = е.
Свойство: а  в
в  ε – обратим в кольце К Þ а
ε – обратим в кольце К Þ а  в ε
в ε
Критерий подкольца: Непустое подмножествоS кольца К является подкольцом тогда и только тогда, когда:
1) ("а, вÎS) а + в Î S │ или ("а, вÎS)
2) ("а ÎS) -а Î S │ 1) а - в Î S
3) ("а, вÎS) а · в Î S │ 2) а · в Î S
Определение 1.11. Кольцо К называется областью целостности, если в нем нет делителей нуля (т.е. если ав = 0, то а = 0  в = 0).
в = 0).
Любое числовое кольцо является областью целостности.
Элементы кольца называются ассоциированными, если а  в
в  в
в  а.
а.
Определение 1.12. Пусть имеется два кольца (К1, +, ∙) и (К2,  ).
).
Отображение ƒ: К1®К2 называется гомоморфизмом колец, если:
1) ƒ (а+в)= ƒ (а)  ƒ (в); 2) ƒ(а·в) = ƒ(а)
ƒ (в); 2) ƒ(а·в) = ƒ(а)  ƒ(в).
ƒ(в).
|
|
|
Гомоморфное взаимно однозначное отображение кольца К1 на кольцо К2 называют изоморфизмом колец.
Так как кольцо является группой, то для колец справедливы все свойства гомоморфизма групп.
Теорема 1.4. Гомоморфный образ кольца является кольцом.
Определение 1.13. Множество элементов кольца К1, переходящее при гомоморфизме ƒ в нуль кольца К2 называется ядром гомоморфизма.
Определение 1.14. Алгебра (Р, +, ∙) – поле, если
1. (Р, +) – абелева группа.
2. (Р\{0}, ∙) – абелева группа.
3. Умножение дистрибутивно относительно сложения.
Простейшие свойства поля:
I. Так как поле является кольцом, то для него справедливы все свойства колец.
II. Свойства, специфические для полей:
а) В поле не существует делителей нуля;
В поле можно ввести операцию деления: 
б) –а = (-1) · а; в)  ; г)
; г)  ;
;
д)  ;
;
е) Критерий равенства дробей  ;
;
ж)  ;
;
з) ас = вс  с ≠ 0
с ≠ 0  а = в; и) ав = 1
а = в; и) ав = 1  а ≠ 0
а ≠ 0  в = а-1
в = а-1
к) ав = 0  а = 0
а = 0  в = 0; л)
в = 0; л)  .
.
Критерий подполя: Непустое подмножествоS поля Р является подполем поля Р тогда и только тогда, когда:
1) ("а, вÎ S) а + в Î S; 2) ("а, вÎ S) а · в Î S;
3) ($а ÎS) -а Î S; 4) ($а ÎS) а-1 Î S.
Определение 1.15. Пусть (Р1, +, ∙), (Р2, +, ∙) – два поля.
Отображение ƒ: Р1®Р2 называется гомоморфизмом полей, если:
1) ƒ (а+в)= ƒ (а) + ƒ (в); 2) ƒ(а·в) = ƒ(а) · ƒ(в)
Теорема 1.5. Гомоморфный образ поля является полем.
Числовое поле – множество, содержащее не менее 2-х элементов, которое замкнуто относительно действий +, -, ·,:.
Наименьшее числовое поле – поле рациональных чисел. Доказать!
Задачи для самостоятельной работы:
1. Докажите, что относительно бинарной операции  множество R не содержит нейтрального элемента.
множество R не содержит нейтрального элемента.
2. Обладает ли множество N правым нейтральным элементом; левым нейтральным элементом; нейтральным элементом относительно бинарной операции, выполняемой по правилу а ◦ b = аb? Обратима ли данная операция на множестве N?
3. Докажите, что относительно бинарной операции, выполняемой по правилу  , множество R+ не обладает нейтральным элементом.
, множество R+ не обладает нейтральным элементом.
4. Покажите, что действие, выполняемое по правилу а◦b = а2 + b2, является коммутативной, но не ассоциативной бинарной операцией на множестве R.
5. Почему множество R не является полугруппой относительно действия, выполняемого по правилу а◦b = а2 + b2 для любых а, b Î R?
6. Докажите, что на множестве Z действие, выполняемое по правилу  , является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система (Z,◦) нейтральным элементом?
, является бинарной, коммутативной, ассоциативной, но необратимой операцией. Обладает ли алгебраическая система (Z,◦) нейтральным элементом?
7. Является ди данное отображение изоморфным отображением указанных алгебр.
а) ƒ: (Z, +) → (Z, +), ƒ(а) = а + 1
б) ƒ: (Q[  ], +) → (Q[
], +) → (Q[ 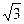 ], +), ƒ(а +b
], +), ƒ(а +b  ) = а + b
) = а + b 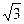
в) ƒ: (Z, +) → (Z, +), ƒ(а) = 2а
г) ƒ: ( , +) → (R, +), ƒ
, +) → (R, +), ƒ 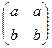 = а + b
= а + b
д) ƒ: (R+, ∙) → (R, +), ƒ(а) = ln а
8. Является ли группой множество чисел вида а + b  относительно сложения, если а и в любые рациональные числа.
относительно сложения, если а и в любые рациональные числа.
9. Является ли множество квадратных трехчленов вида А = {ах2+bх+с а, b, с Î R} группой относительно сложения?
10. Является ли множество (Z, ◦) группой, если а ◦ b = 2а + 3b?
11. Является ли множество М целых чисел, кратных трем подгруппой аддитивной группы Z?
12. Выясните, образует ли поле следующее множество относительно указанной операции.
а) Множество всех матриц вида  , а, b Î Q относительно сложения и умножения матриц;
, а, b Î Q относительно сложения и умножения матриц;
б) Множество чисел вида а + b  с целыми а и b относительно сложения и умножения чисел;
с целыми а и b относительно сложения и умножения чисел;
в) Множество пар (а, b) рациональных чисел относительно бинарных операций, заданных по следующим правилам:
(а,b) + (с,d) = (а+с, b+d) (а,b) · (с,d) = (ас+2bd; аd+bс)
|
|
|


