 |
Классическое и статистическое определение вероятности
|
|
|
|
РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Учебное пособие для студентов специальностей
071900 – Информационные системы и технологии
351400 – Прикладная информатика в сфере сервиса
Составитель
д. т. н., проф. Садыков С. С.
Муром – 2004
СОДЕРЖАНИЕ
ТЕМА 1. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
1.1. Классическое и статистическое определение вероятности................................................. 4
1.2. Геометрические вероятности.................................................................................................. 5
ТЕМА 2. ОСНОВНЫЕ ТЕОРЕМЫ
2.1. Теоремы сложения и умножения вероятностей.................................................................... 7
2.2. Вероятность появления хотя бы одного события................................................................. 9
2.3. Формула полной вероятности.............................................................................................. 10
2.4. Формула Бейеса..................................................................................................................... 11
ТЕМА 3. ПОВТОРЕНИЕ ИСПЫТАНИЙ
3.1. Формула Бернулли................................................................................................................. 12
3.2. Локальная и интегральная теоремы Лапласа..................................................................... 13
3.3. Отклонение относительной частоты от постоянной вероятности
в независимых испытаниях.................................................................................................. 14
3.4. Наивероятнейшее число появлений события в независимых
испытаниях............................................................................................................................ 15
3.5. Производящая функция........................................................................................................ 16
ТЕМА 4. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
4.1. Закон распределения вероятностей дискретной случайной величины.
Законы биномиальный и Пуассона..................................................................................... 17
4.2. Простейший поток событий................................................................................................ 19
|
|
|
4.3. Числовые характеристики дискретных случайных величин........................................... 19
4.4. Теоретические моменты........................................................................................................ 23
ТЕМА 5. ЗАКОН БОЛЬШИХ ЧИСЕЛ
5.1. Неравенство Чебышева......................................................................................................... 24
5.2. Теорема Чебышева................................................................................................................. 25
ТЕМА 6. ФУНКЦИИ И ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН
6.1. Функция распределения вероятностей случайной величины.......................................... 26
6.2. Плотность распределения вероятностей непрерывной
случайной величины............................................................................................................. 27
6.3. Числовые характеристики непрерывных случайных величин........................................ 28
6.4. Равномерное распределение................................................................................................ 31
6.5. Нормальное распределение.................................................................................................. 32
6.6. Показательное распределение и его числовые характеристики...................................... 33
ТЕМА 7. РАСПРЕДЕЛЕНИЕ ФУНКЦИИ ОДНОГО И ДВУХ СЛУЧАЙНЫХ АРГУМЕНТОВ
7.1. Функция одного случайного аргумента............................................................................. 35
7.2. Функция двух случайных аргументов................................................................................ 36
ТЕМА 8. СИСТЕМЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
8.1. Законы распределения двумерной случайно величины.................................................... 38
8.2. Условные законы распределения вероятностей
составляющих дискретной двумерной случайно величины............................................ 40
8.3. Отыскание плотностей и условных законов распределения
составляющих непрерывной двумерной случайно величины......................................... 41
8.4. Числовые характеристики
непрерывной системы двух случайных величин.............................................................. 42
ТЕМА 9. КОРРЕЛЯЦИОННАЯ ТЕОРИЯ СЛУЧАЙНЫХ ФУНКЦИЙ
|
|
|
9.1. Основные понятия. Характеристики случайных функций.............................................. 43
9.2. Характеристики суммы случайных функций.................................................................... 46
9.3. Характеристики производной от случайной функции..................................................... 47
9.4. Характеристики интеграла от случайной функции.......................................................... 48
ТЕМА 10. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ
10.1. Характеристики стационарной случайной функции...................................................... 50
10.2. Стационарно связанные случайные функции................................................................. 50
10.3. Корреляционная функция
производной от стационарной случайной функции....................................................... 51
10.4. Корреляционная функция
интеграла от стационарной случайной функции............................................................ 51
10.5. Взаимная корреляционная функция дифференцируемой
стационарной случайной функции и ее производных................................................... 52
Литература.......................................................................................................................................... 53
ПРИЛОЖЕНИЕ 1. Таблица значений функции φ(x)..................................................................... 54
ПРИЛОЖЕНИЕ 2. Таблица значений функции Ф(х).................................................................... 55
ПРИЛОЖЕНИЕ 3. Таблица значений tγ = t(γ, n)............................................................................ 56
ПРИЛОЖЕНИЕ 4. Таблица значений q = q(γ, n)............................................................................ 57
ПРИЛОЖЕНИЕ 5. Критические точки распределения χ*............................................................ 57
ПРИЛОЖЕНИЕ 6. Критические точки распределения Стьюдента............................................. 58
ПРИЛОЖЕНИЕ 7. Критические точки распределения F Фишера – Снедекора........................ 59
ПРИЛОЖЕНИЕ 8. Критические точки распределения Кочрена................................................. 60
ПРИЛОЖЕНИЕ 9. Равномерно распределенные случайные числа............................................ 62
ПРИЛОЖЕНИЕ 10. Квантили нормального распределения up.................................................... 63
Для заметок......................................................................................................................................... 66
ТЕМА 1. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Классическое и статистическое определение вероятности
При классическом определении вероятность события определяется равенством
где m – число элементарных исходов испытания, благоприятствующих появлению события А; n – общее число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и возможны.
|
|
|
Относительная частота события А определяется равенством
где m – число испытаний, в которых событие А наступило; n – общее число произведённых испытаний.
При статистическом определении в качестве вероятности события принимают его относительную частоту.
1. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях – чётная, причём на грани хотя бы одной из костей появится шестёрка.
Решение. На выпавшей грани «первой» игральной кости может появиться одно очко, два очка, …, шесть очков. Аналогичные шесть элементарных исходов возможны при бросании «второй» кости. Каждый из исходов бросания «первой» кости может сочетаться с каждым из исходов бросания «второй». Таким образом, общее число возможных элементарных исходов испытания равно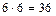 
. Эти исходы образуют полную группу и в силу симметрии костей равновозможны.
Благоприятствующими интересующему нас событию (хотя бы на одной грани появится шестёрка, сумма выпавших очков – чётная) являются следующие пять исходов (первым записано число очков, выпавших на «первой» кости, вторым – число очков, выпавших на «второй» кости; далее найдена сумма очков):
1) 6, 2; 6 + 2 = 8, 2) 6, 4; 6 + 4 = 10, 3) 6, 6; 6 + 6 = 12, 4) 2, 6; 2 + 6 = 8,
5) 4, 6; 4 + 6 = 10.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех возможных элементарных исходов: P = 5/36.
2. При перевозке ящика, в котором содержалось 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причём неизвестно какая. Наудачу извлечения (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.
3. Указать ошибку решения «решения» задачи: брошены две игральные кости; найти вероятность того, что сумма выпавших очков равна 3 (событие А).
«Решение». Возможны два исхода испытания: сумма выпавших очков равна 3, сумма выпавших очков не равна 3. Событию А благоприятствует один исход; общее число исходов равно двум. Следовательно, искомая вероятность P (А) = 1/2.
|
|
|
Ошибка этого «решения» состоит в том, что рассматриваемые исходы не являются равновозможными.
Правильное решение. Общее число равновозможных исходов равно 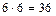(каждое число очков, выпавших на одной кости, может сочетаться со всеми числами очков, выпавших на другой кости). Среди этих исходов благоприятствуют событию А только два исхода (в скобках указаны числа выпавших очков): (1; 2) и (2; 1). Следовательно, искомая вероятность P (А) = 2/36 = 1/18.
4. Найти вероятность того, что при бросании трёх игральных костей шестёрка выпадет на одной (безразлично какой) кости, если на гранях двух других костей выпадут числа очков, не совпадающие между собой (и не равные шести).
5. В ящике 10 одинаковых деталей, помеченных номерами 1, 2, …, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлечённых деталей окажутся: а) деталь №1; б) детали №1 и №2.
6. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлечённые детали окажутся окрашенными.
7. В конверте среди 100 фотокарточек находится одна разыскиваемая. Из конверта наудачу извлечены 10 карточек. Найти вероятность того, что среди них окажется нужная.
8. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены четыре детали. Найти вероятность того, что среди извлечённых деталей: а) нет бракованных; б) нет годных.
9. В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.
10. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.
11. На складе имеется 15 кинескопов, причём 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода.
12. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.
13. Отдел технического контроля обнаружил пять бракованных книг в партии из случайно отобранных 100 книг. Найти относительную частоту появления бракованных книг.
14. По цели произведено 20 выстрелов, причём зарегистрировано 18 попаданий. Найти относительную частоту попаданий в цель.
15. При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найти число годных приборов, если всего было проверено 200 приборов.
|
|
|
|
|
|
