 |
Функция распределения вероятностей случайной величины
|
|
|
|
Функцией распределения называют функцию F(х), определяющую для каждого значения х вероятность того, что случайная величина X примет значение, меньшее х, т. е.
F(х) = P(X < x).
Часто вместо термина «функция распределения» используют термин «интегральная функция распределения».
Функция распределения обладает следующими свойствами:
Свойство 1. Значения функции распределения принадлежат отрежу [0; 1]:
0 ≤ F(х) ≤ 1.
Свойство 2. Функция распределения есть неубывающая функция:
F(x2) ≥ F(x1), если x2 > x1.
Следствие 1. Вероятность того, что случайная величина X примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:
P(a < X < b) = F(b) – F(a).
Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, например х1, равна нулю:
P(X = x1) = 0.
Свойство 3. Если все возможные значения случайной величины Х принадлежат интервалу (a, b), то
F(x) = 0 при x ≤ a; F(x) = 1 при x ≥ b.
Следствие. Справедливы следующие предельные соотношения:
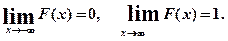
Свойство 4. Функция распределения непрерывна слева:

149. Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале (0, 1/3).
Решение. Вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: P(a < X < b) = F(b) – F(a). Положив a = 0, b = 1/3, получим
P(0 < X < 1/3) = F(1/3) – F(0) =
= [(3/4)x + 3/4]x = 1/3 – [(3/4)x + 3/4]x = 0 = 1/4.
150. Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания X примет значение: а) меньшее 0,2; б) меньшее трех; в) не меньшее трех; г) не меньшее пяти.
|
|
|
151. Случайная величина X задана на всей оси Ох функцией распределения F(x) = 1/2 + (1/π) arctg(x/2). Найти возможные значения х1, удовлетворяющее условию: с вероятностью 1/4 случайная величина Х в результате испытания примет значение, большее х1.
152. Дискретная случайная величина Х задана законом распределения
X 2 4 7
p 0,5 0,2 0,3
Найти функцию распределения F(x) и начертить её график.
153. Дискретная случайная величина Х задана законом распределения
X 3 4 7 10
p 0,2 0,1 0,4 0,3
Найти функцию распределения F(x) и начертить её график.
6.2. Плотность распределения вероятностей
непрерывной случайной величины
Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:  .
.
Часто вместо термина «плотность распределения» используют термины «плотность вероятностей» и «дифференциальная функция».
Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), определяется равенством

Зная плотность распределения, можно найти функцию распределения 
Плотность распределения обладает следующими свойствами:
Свойство 1. Плотность распределения неотрицательна, т. е. f(x) ≥ 0.
Свойство 2. Несобственный интеграл от плотности распределения в пределах от – ∞ до ∞ равен единице:  .
.
В частности, если все возможные значения случайной величины принадлежат интервалу (a, b), то  .
.
154. Дана функция распределения непрерывной случайной величины Х

Найти плотность распределения f(x).
Решение. Плотность распределения равна первой производной от функции распределения:

Заметим, что при х = 0 производная  не существует.
не существует.
155. Дана функция распределения непрерывной случайной величины Х

Найти плотность распределения f(x).
156. Непрерывная случайная величина Х заданная плотностью распределения f(x) = (3/2)sin 3x в интервале (0, π/3); вне этого интервала f(x) = 0. Найти вероятность того, что Х примет значение, принадлежащее интервалу (π/6, π/4).
|
|
|
157. Задана плотность распределения непрерывной случайной величины Х:
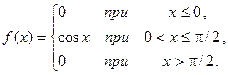
Найти функцию распределения F(x).
158. Задана плотность распределения непрерывной случайной величины Х:

Найти функцию распределения F(x).
159. Плотность распределения непрерывной случайной величины Х задана на всей оси Ох равенством  . Найти постоянный параметр С.
. Найти постоянный параметр С.
|
|
|


