Геометрические вероятности

 

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством

.

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Если предположить, что вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от её расположения относительно G, ни от формы g, то вероятность попадания точки в фигуру g определяется равенством

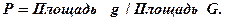
Аналогично определяется вероятность попадания точки в пространственную фигуру v, которая составляет часть фигуры V:

 

16. На отрезке L длины 20 см помещён меньший отрезок l длины 10 см. Найти вероятность того, что точка, наудачу поставленная на большой отрезок, попадёт также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

17. На отрезок ОА длины L числовой оси Ox наудачу поставлена точка B(x). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую, чем L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

18. В круг радиуса R помещён меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадёт также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.

19. На отрезке ОА длины L числовой оси Ox наудачу поставлены две точки: B(x) и C(y), причём y ≥ x. (Координата точ ки С для удобства дальнейшего изложения обозначена через y). Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ (рис. 1, а). Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

 

Решение. Координаты точек В и С должны удовлетворять неравенствам . Введём в рассмотрение прямоугольную систему координат xOy. В этой системе указанным неравенствам удовлетворяют координаты любой точки, принадлежащей прямоугольному треугольнику ОКМ (рис. 1, б). Таким образом, этот треугольник можно рассматривать как фигуру G, координаты точек которой представляют соответственно все возможные значения координат точек B и С.

Рис.1

Длина отрезка ВС должна быть меньше длины отрезка ОВ, т. е. Должно иметь место неравенство , или 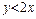. Последнее неравенство выполняется для координат тех точек фигуры G (прямоугольного треугольника ОКМ), которые лежат ниже прямой y = 2x (прямая ON). Как видно из рис. 1, б, все эти точки принадлежат заштрихованному треугольнику ONM. Таким образом, этот треугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими интересующему нас событию (длина отрезка ВС меньше длины отрезка ОВ).

Искомая вероятность

 

20. Задача Бюффона (французский естествоиспытатель XVIII в.). Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2a. На плоскость наудачу бросают иглу длины 2l (l < a). Найти вероятность того, что игла пересечёт какую-нибудь прямую.

21. На отрезке ОА длины L числовой оси Ox наудачу поставлены две точки: B(x) и C(y). Найти вероятность того, что из трёх получившихся отрезков можно построить треугольник.

22. В сигнализатор поступают сигналы от двух устройств, причём поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t (t < T). Найти вероятность того, что сигнализатор срабатывает за время T, если каждое из устройств пошлёт по одному сигналу.

ТЕМА 2. ОСНОВНЫЕ ТЕОРЕМЫ

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: