Теоремы сложения и умножения вероятностей

 

Теорема сложения вероятностей несовместимых событий. Вероятность появления одного из двух несовместимых, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р(А) + Р(В).

Следствие. Вероятность появления одного из нескольких попарно несовместимых событий, безразлично какого, равна сумме вероятностей этих событий:

P(A₁ + A₂ + … + A_n) = P(A₁) + P(A₂) +… + P(A_n).

Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A + B) = P(A) + P(B) – P(AB).

Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий

P(A + B + C) = P(A) + P(B) + P(C) – P(AB) – P(AC) – P(BC) + P(ABC).

Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

P(AB) = P(A) * P_A(B).

В частности, для независимых событий

P(AB) = P(A) * P(B),

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причём вероятность каждого последующего события вычисляют в предложении, что все предыдущие события уже наступили:

где 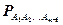– вероятность события A_n, вычисленная в предложении, что события A₁, A₂, …, A_n-1 наступили.

В частности, вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

P(A₁A₂…A_n) = P(A₁) * P(A₂)…P(A_n).

 

23. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причём пять из них в переплёте. Библиотекарь берёт наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплёте (событие А).

 

Решение. Первый способ. Требование – хотя бы один из трёх взятых учебников в переплёте – будет осуществлено, если произойдёт любое из следующих трёх несовместимых событий: В – один учебник в переплёте, С – два учебника в переплёте, D – три учебника в переплёте.

Интересующее нас событие А можно представить в виде суммы событий: A = B + C + D. По теореме сложения,

P(A) = P(B) + P(C) + P(D). (*)

Найдём вероятности событий B, C и D:

Подставив эти вероятности в равенство (*), окончательно получим

Р(А) = 45/91 + 20/91 + 2/91 = 67/91.

Второй способ. События А (хотя бы один из взятых трёх учебников имеет переплёт) и (ни один из взятых учебников не имеет переплёта) – противоположные, поэтому (сумма вероятностей двух противоположных событий равна единице). Отсюда .

Вероятность появления события (ни один из взятых учебников не имеет переплёта)

.

Искомая вероятность

.

24. В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три летали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.

25. доказать, что если событие А влечёт за собой событие В, то Р(В) ≥ Р(А).

 

Решение. Событие В можно представить в виде суммы несовместных событий А и .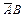

По теореме сложения вероятностей несовместных событий получим

.

Так как , то Р(В) ≥ Р(А).

 

26. Вероятности появления каждого из двух независимых событий А₁ и А₂ соответственно равны р₁ и р₂. Найти вероятность появления только одного из этих событий.

27. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

28. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.

29. Сколько надо бросить игральных костей, чтобы с вероятностью, меньшей 0,3, можно было ожидать, что ни на одной из выпавших граней не появится шесть очков?

 

Решение. Введём обозначения событий: А – ни на одной из выпавших граней не появится 6 очков; А_i – на выпавшей грани i -й кости (i = 1, 2, …, n) не появится 6 очков.

Интересующее нас событие А состоит в совмещении событий А₁, А₂, …, А_n, т. е. А = А₁А₂…А_n.

Вероятность того, что на любой выпавшей грани появится число очков, не равное шести, равна Р(А_i) = 5/6.

События А_i независимы в совокупности, поэтому применима теорема умножения:

По условию, (5/6)ⁿ < 0,3. Следовательно, . Отсюда, учитывая, что log(5/6) < 0, найдём: n > 6,6. Таким образом, искомое число игральных костей n ≥ 7.

 

30. Вероятность попадания в мишень стрелком при одном выстреле равна 0,8. сколько выстрелов должен произвести стрелок, чтобы с вероятностью, меньшей 0,4, можно было ожидать, что не будет ни одного промаха?

31. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплёте. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплёте.

32. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билеты окажутся выигрышными.

33. В цехе работают семь мужчин и три женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.

34. В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что все извлечённые детали окажутся окрашенными.

35. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.

36. По данным переписи населения (1891 г.) Англии и Уэльса установлено: темноглазые отцы и темноглазые сыновья (АВ) составили 5% обследованных лиц, темноглазые отцы и светлоглазые сыновья , светлоглазые отцы и темноглазые сыновья , светлоглазые отцы и светлоглазые сыновья 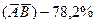. Найти связь между цветом глаз отца и сына.

37. Найти вероятность по данным вероятностям: P(A) = a, P(B) = b, P(A + B) = c.

38. Найти вероятность по данным вероятностям: P(A) = a, P(B) = b, P(A + B) = c.

39. Наступление события АВ необходимо влечёт наступления события С. Доказать, что .

40. Доказать, что

.

Предполагается, что Р(А) > 0.

41. Наступление события АВС необходимо влечёт наступление события D. Доказать, что

.

42. Вывести теорему сложения вероятностей для трёх совместных событий:

.

Предполагается, что для двух совместных событий теорема сложения уже доказана:

.

43. Даны три попарно независимых события А, В, С, которые, однако, все три вместе произойти не могут. Предполагая, что все они имеют одну и ту же вероятность р, найти наибольшее возможное значение р.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: