 |
Функция одного случайного аргумента
|
|
|
|
Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X и записывают Y = j(X).
Если X – дискретная случайная величина и функция Y = j(X) монотонна, то различным значениям X соответствуют различные значения Y, причем вероятности соответствующих значений X и Y одинаковы. Другими словами, возможные значения Y находят из равенства
yi = j(xi),
где xi – возможные значения X; вероятности возможных значений Y находят из равенства
P(Y = yi) = P(X = xi).
Если же Y = j(X) – немонотонная функция, то, вообще говоря, Различным значениям X могут соответствовать одинаковые значения Y (так будет, если возможные значения X попадут в интервал, в котором функция j(X) не монотонна). В этом случае для отыскания вероятностей возможных значений Y следует сложить вероятности тех возможных значений X, при которых Y принимает одинаковые значения. Другими словами, вероятность повторяющегося значения Y равна сумме вероятностей тех возможных значений X, при которых Y принимает одно и то же значение.
Если X – непрерывная случайная величина, заданная плотностью распределения f(х), и если у = j(х) – дифференцируемая строго возрастающая или строго убывающая функция, обратная функция которой x = y(у), то плотность распределения g(y) случайной величины Y находят из равенства
g(y) = f[y(y)] ∙ [y'(y)].
Если функция у = j(х) в интервале возможных значений X не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция j(х) монотонна, и найти плотности распределений gi(у) для каждого из интервалов монотонности, а затем представить g(у) в виде суммы:
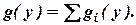
Например, если функция j(х) монотонна в двух интервалах, в которых соответствующие обратные функции равны y1(у) и y2(у), то
|
|
|
207. Дискретная случайная величина X задана законом распределения:
| X | |||
| p | 0,4 | 0,1 | 0,5 |
Найти закон распределения случайной величины Y = 3Х.
Решение. Найдем возможные значения величины Y = 3X. Имеем: y1 =3∙1=3; у2= 3∙3=9; у3 =3∙5=15. Видим, что различным возможным значениям X соответствуют различные значения Y. Это объясняется тем, что функция у=j(х)= 3х монотонна. Найдем вероятности возможных значении Y. Для того чтобы Y = у1 = 3 достаточно, чтобы величина X приняла значение х1 =1. Вероятность же события Х =1 по условию равна 0,4; следовательно, и вероятность события Y = у1 =3 также равна 0,4.
Аналогично получим вероятности остальных возможных значений Y:
p (Y = 9) = p (Х = 3) = 0,1;
p (Y = 15) = p(Х = 5) = 0,5.
Напишем искомый закон распределения Y:
| Y | |||
| p | 0,4 | 0,1 | 0,5 |
208. Дискретная случайная величина X задана законом распределения:
| X | |||
| p | 0,2 | 0,1 | 0,7 |
Найти закон распределения случайной величины Y=2X +1.
209. Дискретная случайная величина X задана законом распределения:
| X | -1 | -2 | ||
| p | 0,3 | 0,1 | 0,2 | 0,4 |
Найти закон распределения случайной величины Y=X2.
210. Дискретная случайная величина X задана законом распределения:
| X | p/4 | p/2 | 3 p/4 |
| p | 0,2 | 0,7 | 0,1 |
Найти закон распределения случайной величины Y=sinX.
211. Задана плотность распределения f(x) случайной величины X, возможные значения которой заключены в интервале (a, b). Найти плотность распределения случайной величины Y=3X.
212. В прямоугольной системе координат xOy из точки A (4,0) наудачу (под произвольным углом t) проведен луч, пересекающий ось Oy. Найти дифференциальную функцию g( y) распределения вероятностей ординаты y точки пересечения проведенного луча с осью Oy.
213. Случайная величина X равномерно распределена в интервале (-p/2, p/2). Найти плотность распределения g(y) случайной величины Y=sinX.
|
|
|
214. Случайная величина X распределена равномерно в интервале (0, 2p). Найти плотность распределения g(y) случайной величины Y=cosX.
215. Случайная величина X распределена нормально с математическим ожиданием, равным a, и средним квадратическим отклонением, равным s. Доказать, что линейная функция Y=AX+B также распределена нормально, причем M(Y)=Aa+B, s(Y)=|A|s.
216. Задана плотность 
нормально распределенной случайной величины X. Найти плотность распределения g(y) случайной величины Y=X2.
217. Случайная величина X задана плотность распределения f(x)=(1/2)sinx в интервале (0, p); вне этого интервала f(x) =0. Найти математическое ожидание случайной величины Y=j(X)=X2, определив предварительно плотность распределения g(Y) величины Y.
218. Случайная величина X задана плотностью распределения f(x)=(1/2)sinx в интервале (0, p); вне этого интервала f(x) =0. Найти дисперсию функции Y=j(X)=X2, используя плотность распределения g(y).
219. Задана функция распределения F(x) случайной величины X. Найти функцию распределения G(y) случайной величины Y=3X+2.
220. Задана функция распределения F(x) случайной величины X. Найти функцию распределения G(y) случайной величины Y=-(2/3)X+2.
|
|
|
